Vlastnosti logaritmických funkcií, príklady, cvičenia

Ten logaritmická funkcia Je to matematický vzťah, ktorý spája každé pozitívne skutočné číslo X S logaritmom a na základni do. Tento vzťah spĺňa požiadavky na funkciu: každý prvok X patriaci k doméne má jedinečný obraz.

Preto:

f (x) = y = log_do X , S> 0 a odlišným od 1.

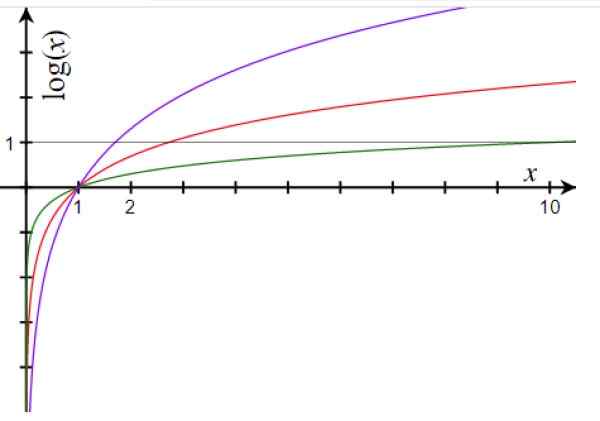
postava 1. Graf funkcie logaritmu pre základňu 10 (zelená), základňa E (červená) a základňa 1.7 (fialová). Zdroj: Wikimedia Commons.

Hlavné vlastnosti logaritmickej funkcie sú:

-Jeho doména sú všetky reais väčšie ako 0, okrem 0. Inými slovami, na žiadnej základni neexistuje žiadny logaritmus ani záporné čísla. Vo forme intervalu:

slnko _F = (0, ∞+)

-Logaritmus čísla môže byť negatívny, pozitívny alebo 0, takže jeho rozsah alebo trasa je:

Rggo _F = (-∞, ∞+)

-Logaritmická funkcia vždy rastie pre> 1 a klesá<1.

-Inverzia f (x) = log_do X je exponenciálna funkcia.

Funkcia logaritmu založená na logaritme je skutočne inverznou funkciou potenciálnej funkcie:

F^-1(x) = a^a

Od založenia logaritmu do číslo X, Je to číslo a na ktoré musí byť základňa zdvihnutá do získať X.

-Základný logaritmus je vždy 1. Teda graf f (x) = log_do X Vždy sa pretínajte k osi x v bode (1,0)

-Logaritmická funkcia je transcendentný a nemožno ich vyjadriť ako polynóm alebo ako kvocient z nich. Okrem logaritmu táto skupina zahŕňa okrem iného aj trigonometrické a exponenciálne funkcie.

[TOC]

Príklady

Logaritmická funkcia je možné stanoviť prostredníctvom rôznych základov, ale najpoužívanejšie sú 10 a a, kde a Je to počet Euler rovnajúci sa 2 71828 .. .

Keď sa používa základňa 10, logaritmus sa nazýva desatinný logaritmus, vulgárny logaritmus, briggs alebo jednoducho logaritmus na sušenie.

A ak sa používa číslo E, potom sa nazýva Neperian Logaritmus, Johnom Napier, škótsky matematik, ktorý objavil logaritmy.

Môže vám slúžiť: Multiplikatívna inverzia: Vysvetlenie, príklady, vyriešené cvičenia

Zápis, ktorý sa používa pre každú z nich, je nasledovne:

-Logaritmus desatinného priestoru: denník₁₀ x = log x

-Neperian Logaritmus: ln x

Keď sa použije iná základňa, je to absolútne nevyhnutné. Napríklad, ak ide o logaritmy na základni 2, je napísané:

y = denník₂ X

Pozrime sa na logaritmus číslo 10 v troch rôznych základniach, aby som ilustroval tento bod:

Log 10 = 1

ln 10 = 2.30259

protokol₂ 10 = 3.32193

Bežné kalkulačky prinášajú iba desatinné logaritmy (log) a neperiánsky logaritmus (funkcia LN). Na internete existujú kalkulačky s inými základňami. V každom prípade môže čitateľ overiť, pomocou toho istého, že s predchádzajúcimi hodnotami je splnený:

10¹ = 10

a^2.3026 = 10.0001

2^3.32193 = 10.0000

Malé desatinné rozdiely sú spôsobené množstvom desatinných miest pri výpočte logaritmu.

Výhody logaritmov

Medzi výhody používania logaritmov patrí ľahkosť, ktorú poskytujú pri práci s veľkým počtom, pomocou svojho logaritmu namiesto čísla priamo.

Je to možné, pretože funkcia logaritmu rastie pomalšie, pretože čísla sú väčšie, ako si vážime v grafike.

Takže aj v prípade veľmi veľkého počtu sú ich logaritmy omnoho menšie a manipulácia s malými číslami je vždy jednoduchšia.

Logaritmy okrem toho spĺňajú nasledujúce vlastnosti:

-Produkt: log (a.b) = log a + log b

-Kvocient: log (a/b) = log a - log b

-Moc: log a^b = b.protokol a

Týmto spôsobom sa výrobky a kvocienty stávajú sumami a odčítaním menších počtov, zatiaľ čo potenciácia sa transformuje na jednoduchý produkt, hoci sila je vysoká.

Z tohto dôvodu logaritmy umožňujú vyjadriť čísla, ktoré sa líšia vo veľmi veľkých rozsahoch hodnôt, ako je intenzita zvuku, pH roztoku, jas hviezd, elektrický odpor a intenzita zemetrasení na Richter mierka.

Môže vám slúžiť: externé alternatívne uhly: Cvičenia a cvičenia vyriešenéObrázok 2. Logaritmy sa používajú na stupnici Richter na kvantifikáciu veľkosti zemetrasení. Obrázok ukazuje, že budova sa zrútila v Concepción v Čile počas zemetrasenia v roku 2010. Zdroj: Wikimedia Commons.

Pozrime sa na príklad spracovania vlastností logaritmov:

Príklad

Nájdite hodnotu X v nasledujúcom výraze:

log (5x +1) = 1 + log (2x-1)

Odpoveď

Máme tu logaritmickú rovnicu, vzhľadom na skutočnosť, že neznámy je v argumente logaritmu. Vyrieši sa tým, že ponecháva jeden logaritmus na každej strane rovnosti.

Začneme umiestnením všetkých výrazov, ktoré obsahujú „x“ naľavo od rovnosti, a tie, ktoré obsahujú iba čísla vpravo:

log (5x+1) - log (2x -1) = 1

Vľavo máme odčítanie dvoch logaritmov, ktoré možno písať ako logaritmus kvocientu:

log [(5x+1)/ (2x-1)] = 1

Napravo je však číslo 1, ktoré môžeme vyjadriť ako log 10, ako sme už predtým videli. Tak:

log [(5x+1)/ (2x-1)] = log 10

Aby sa rovnosť splnila, argumenty z logaritmov musí byť rovnaké:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Cvičenie aplikácie: Richterová stupnica

V roku 1957 sa v Mexiku vyskytlo zemetrasenie, ktorého veľkosť bola 7.7 v Richterovej stupnici. V roku 1960 sa v Čile vyskytlo ďalšie zemetrasenie veľkosti, 9.5.

Vypočítajte, koľkokrát bolo čílske zemetrasenie intenzívnejšie ako zemetrasenie v Mexiku, s vedomím, že veľkosť m_R Na stupnici Richtera je daný vzorcom:

M_R = log (10⁴ Jo)

Riešenie

Veľkosť v Richterovej stupnici zemetrasenia je logaritmická funkcia. Budeme vypočítať intenzitu každého zemetrasenia, pretože máme Richter veľkosti. Urobme to krok za krokom:

Môže vám slúžiť: Primo čísla: Charakteristiky, príklady, cvičenia

-Mexiko: 7.7 = protokol (10⁴ Jo)

Keďže inverzia funkcie logaritmu je exponenciálna, aplikujeme to na obidvoch stranách rovnosti s úmyslom vyčistiť I, ktorý sa nachádza v argumente logaritmu.

Pretože sú to desatinné logaritmy, základňa je 10. Tak:

V pravom období, 10 a log (10⁴ I) sú zrušené (rovnako ako v prípade štvorcového a druhého koreňa), bytie: Odchádzanie:

10 ^7.7 = 10⁴ Jo

Intenzita zemetrasenia v Mexiku bola:

Jo_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Chilli: 9.5 = log (10⁴ Jo)

Rovnaký postup nás vedie k intenzite čílskeho zemetrasenia I_Chvály:

Jo_Chvály = 10 ^9.5 / 10⁴ = 10^5.5

 Teraz môžeme porovnávať obe intenzity:

Jo_Chvály / Jo_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 Jo_Chvály = 63.1. Jo_M

Chileovo zemetrasenie bolo asi 63 -krát intenzívnejšie ako Mexiko. Pretože veľkosť je logaritmická, rastie pomalšie ako intenzita, takže rozdiel 1 v veľkosti znamená 10 -krát väčšiu amplitúdu seizmickej vlny.

Rozdiel medzi veľkosťami oboch zemetrasení je 1.8, preto by sme mohli očakávať rozdiel v intenzitách bližšie k 100 ako 10, ako sa stalo účinne.

V skutočnosti, ak by bol rozdiel presne 2, čílske zemetrasenie by bolo 100 -krát intenzívnejšie ako Mexičan.

Odkazy

1. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
2. Figuera, J. 2000. Matematika 1. Diverzifikovaný rok. Edície Co-Bo.
3. Jiménez, r. 2008. Algebra. Sála.
4. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
5. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.