Absolútny frekvenčný vzorec, výpočet, distribúcia, príklad

Ten Absolútna strava Je definovaný ako počet, koľkokrát sa rovnaké údaje opakujú v rámci súboru pozorovaní numerickej premennej. Súčet všetkých absolútnych frekvencií je rovnocenný s celkovým počtom údajov.

Ak existuje veľa hodnôt štatistickej premennej, je vhodné ich správne zorganizovať, aby ste extrahovali informácie o svojom správaní. Takéto informácie sa uvádzajú podľa ústredných tendencií a opatrení na dispergáciu.

postava 1. Absolútna frekvencia štatistického pozorovania je kľúčom k nájdeniu trendu, ktorý sleduje súbor údajov

Pri výpočtoch týchto opatrení sú údaje reprezentované prostredníctvom frekvencie, s akou sa objavujú vo všetkých pozorovaniach.

Nasledujúci príklad ukazuje, ako je odhalenie absolútnej frekvencie každého údajov. V prvej polovici mája to boli veľkosti najlepších kokteilových kostýmov, známeho dámskeho oblečenia: sklad:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Koľko šiat sa predáva v konkrétnej veľkosti, napríklad veľkosť 10? Majitelia majú záujem vedieť, že vydávajú objednávky.

Objednávanie údajov sa dá ľahšie počítať, celkovo je presne 30 pozorovaní, ako je objednané od najmenších po najvyššie, ako je tento:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

A teraz je zrejmé, že veľkosť 10 sa opakuje 6 -krát, preto sa jej absolútna frekvencia rovná 6. Rovnaký postup sa vykonáva s cieľom zistiť absolútnu frekvenciu zostávajúcich veľkostí.

[TOC]

Vzorce

Absolútna frekvencia označená ako f_Jo, Rovná sa to počtu násobku ako určitá hodnota x_Jo je v skupine pozorovaní.

Za predpokladu, že celkové pozorovania sú hodnoty n, súčet všetkých absolútnych frekvencií sa musí rovnať uvedenému číslu:

Môže vám slúžiť: Papomudas

∑f_Jo = f₁ + F₂ + F₃ +... f_n = N

Iné frekvencie

Ak každá hodnota f_Jo Je vydelený celkovým počtom údajov n, máte relatívna frekvencia F_r hodnoty x_Jo:

F_r = f_Jo / N

Relatívne frekvencie sú hodnoty medzi 0 a 1, pretože n je vždy väčšie ako akékoľvek f_Jo, Ale suma sa musí rovnať 1.

Násobením 100 do každej hodnoty f_r Máte Relatívna percentuálna frekvencia, ktorého suma je 100%:

Relatívna percentuálna frekvencia = (f_Jo / N) x 100%

Je to tiež dôležité akumulovaná frekvencia F_Jo Až do určitého pozorovania je to súčet všetkých absolútnych frekvencií, kým sa uvedené pozorovanie vrátane:

F_Jo = f₁ + F₂ + F₃ +... f_Jo

Ak je akumulovaná frekvencia vydelená celkovým počtom údajov n, máte akumulovaná relatívna frekvencia, ktoré sa vynásobia na 100 výsledkov v akumulované percento relatívnej frekvencie.

Ako získať absolútnu frekvenciu?

Ak chcete nájsť absolútnu frekvenciu určitej hodnoty, ktorá patrí do súboru údajov, všetky sú usporiadané od najmenej k najväčšiemu a hodnota sa počíta od.

V príklade veľkostí šiat je absolútna frekvencia veľkosti 4 3 šaty, to je f₁ = 3. Pre veľkosť 6 sa predali 4 šaty: f₂ = 4. Vo veľkosti 8 4 sa predali šaty, f₃ = 4 a tak ďalej.

Tabuľka

Celkové výsledky môžu byť reprezentované v tabuľke, ktorá ukazuje absolútne frekvencie každého z nich:

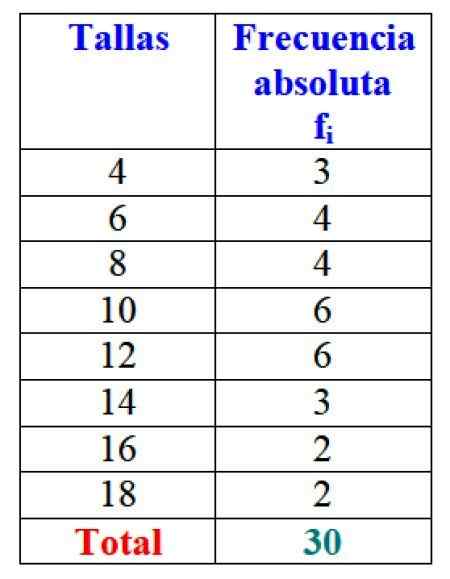Obrázok 2. Tabuľka, ktorá predstavuje premennú „predaný predaj“ a príslušné absolútne frekvencie. Zdroj: f. Zapata.

Je zrejmé, že je výhodné objednať si informácie a mať k nim prístup, namiesto práce s voľnými údajmi.

Dôležitý: Všimnite si, že pridaním všetkých hodnôt stĺpca F_Jo  Celkový počet údajov sa vždy získava. Ak nie, musí sa účtovníctvo skontrolovať, pretože existuje chyba.

Predĺžená frekvenčná tabuľka

Predchádzajúcu tabuľku sa dá rozšíriť pridaním ďalších typov frekvencie v nasledujúcich stĺpcoch doprava:

Môže vám slúžiť: homocedasticita: čo je, dôležitosť a príklady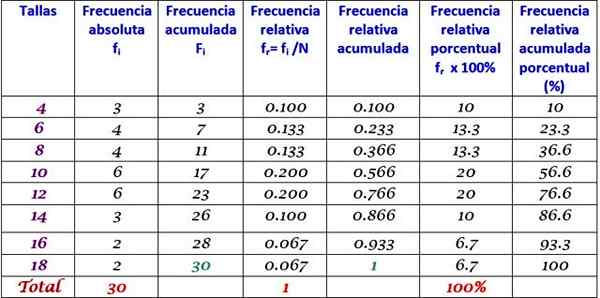

Distribúcia frekvencie

Distribúcia frekvencie je výsledkom organizácie údajov z hľadiska ich frekvencií. Pri práci s mnohými údajmi je vhodné ich zoskupiť do kategórií, intervalov alebo tried, z ktorých každá má svoje príslušné frekvencie: absolútne, relatívne, akumulované a percentuálne podiely.

Cieľom ich vykonania je ľahšie získať prístup k informáciám, ktoré údaje obsahujú, a tiež ich správne interpretovať, čo nie je možné, keď sú prezentované bez objednávky.

V príklade veľkostí nie sú údaje zoskupené, pretože nie sú príliš veľa veľkostí a dajú sa ľahko manipulovať a počítať. Týmto spôsobom sa dajú spracovať aj kvalitatívne premenné.

Distribúcia frekvencie pre zoskupené údaje

Na zoskupenie údajov do tried rovnakej veľkosti sa musí zvážiť nasledujúce:

-Veľkosť, šírka alebo amplitúda triedy: Je to rozdiel medzi najväčšou hodnotou triedy a maloletým.

Veľkosť triedy sa rozhoduje vydelením rozsahu r počtom tried, ktoré treba zvážiť. Rozsah je rozdiel medzi maximálnou hodnotou údajov a maloletým, ako je tento:

Veľkosť triedy = rozsah / počet tried.

-Limit triedy: interval, ktorý prechádza z dolnej hranice na hornú hranicu triedy.

-Značka triedy: Je to stred intervalu, ktorý sa považuje za reprezentatívny pre triedu. Vypočítava sa s polopriepustným obmedzením hornej hranice a dolnou hranicou triedy.

-Počet tried: Stuges je možné použiť:

Triedy = 1 + 3 322 log n

Kde n je počet tried. Ako zvyčajne je desatinné číslo, nasledujúce je zaokrúhlené.

Príklad

Veľký továrenský stroj je mimo prevádzky, pretože má opakujúce sa zlyhania. Po sebe idúce obdobia nečinnosti v minútach, uvedeného stroja, sú zaznamenané nižšie, s celkom 100 údajmi:

Môže vám slúžiť: Pravdepodobnosť frekvencie: koncept, ako sa vypočíta a príklady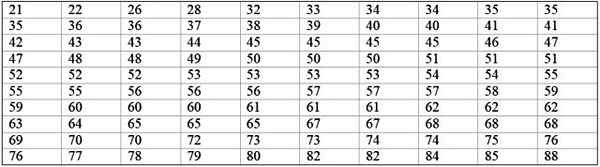

Najprv je určený počet tried:

Triedy = 1 + 3 322 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Veľkosť triedy = rozsah / počet tried = (88-21) / 8 = 8.375

Je to tiež desatinné číslo, takže to trvá 9 ako veľkosť triedy.

Značka triedy je priemer medzi hornou a dolnou hranicou triedy, napríklad pre triedu [20-29), je známka:

Značka triedy = (29 + 20) / 2 = 24.5

Postupujte rovnakým spôsobom, aby ste našli značky tried zostávajúcich intervalov.

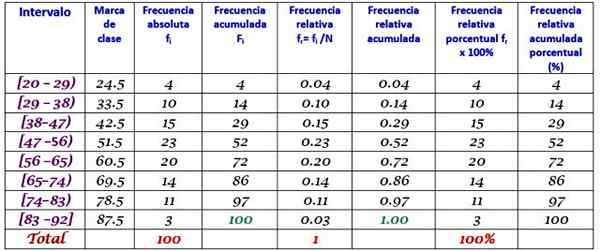
Cvičenie

40 mladých ľudí uviedlo, že čas v minútach, ktorý prešiel minulú nedeľu na internete, bol ďalším, čoraz viac si objednal:

0; 12; dvadsať; 35; 35; 38; 40; Štyri. Päť; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Žiada sa o vytvorenie frekvenčnej distribúcie týchto údajov.

Riešenie

Rank R súboru n = 40 údajov je:

R = 220 - 0 = 220

Uplatňovanie vzorca Sturges na určenie počtu tried poskytuje tento výsledok:

Triedy = 1 + 3 322 log n = 1 + 3.32 log 40 = 6.3

Rovnako ako desatinné miesto, bezprostredný celok je 7, preto sú údaje zoskupené do 7 tried. Každá trieda má šírku:

Veľkosť triedy = rozsah / počet tried = 220/7 = 31.4

Hodnota blízkej a okrúhle je 35, preto je vybraná šírka triedy 35.

Značky triedy sa vypočítavajú v priemere hornej a dolnej hranice každého intervalu, napríklad pre interval [0,35):

Značka triedy = (0+35)/2 = 17.5

Pokračujeme rovnakým spôsobom so zostávajúcimi triedami.

Nakoniec sa frekvencie vypočítajú podľa vyššie opísaného postupu, čo vedie k nasledujúcemu rozdeleniu:

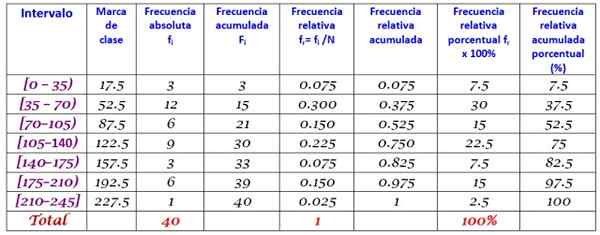
Odkazy

1. Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
4. Spiegel, m. 2009. Štatistika. Séria Schaum. 4 ta. Vydanie. McGraw Hill.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.