Typy zlomkov, príklady, cvičenia vyriešené

Ten zlomky ani frakčné čísla Sú to tie čísla, ktoré sú znázornené, čo naznačuje kvocient medzi dvoma celkovými číslami do a b, tak dlho b sa líši od 0. Napríklad 1/3 je zlomok, ktorý sa znie ako „jedna tretina“.

Na číslo do Je to známe ako čitateľ zlomku a b ako menovateľ To isté. Menovateľ označuje v tom, koľko častí je celok rozdelený. Čitateľ naznačuje, koľko častí tohto celku.

postava 1. Koľko porcií má táto čokoládová tyčinka? Zdroj: piqsels.

Celkom je čokoľvek, čo sa chce rozdeliť alebo zlomiť, napríklad pizza alebo čokoládová tyčinka znázornená na obrázku 1. Bar je vyrobený takým spôsobom, že je veľmi ľahké ho rozdeliť na 5 rovnakých častí, kde sa každá časť rovná 1/5 plného baru.

Vo frakcii alebo zlomkovom čísle 1/5 má čitateľ hodnotu 1 a menovateľ má hodnotu 5. Frakcia znie „piaty“.

Predpokladajme, že jeme 3 kusy čokolády. Povedali by sme, že sme jedli 3/5 častí baru a 2/5 dielov sa ponechajú zdieľať s priateľom. Môžeme tiež povedať, že sme jedli „Tri pätinu čokolády“ a dali sme priateľovi „dve pätiny“.

Grafické znázornenie týchto frakčných čísel je nasledujúce:

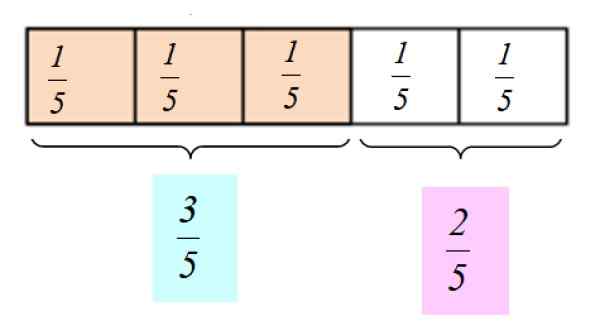Obrázok 2.- Grafické znázornenie zlomkov 3/5 a 2/5. Zdroj: f. Zapata.

[TOC]

Typy zlomkov

Vlastné zlomky

Frakcia je jej vlastná, keď je čitateľ menší ako menovateľ, a preto je jeho hodnota menšia ako 1. Frakcie predchádzajúcej časti, v príklade čokolády, sú ich vlastné zlomky.

Ďalšie príklady ich vlastných zlomkov sú: ½; 8/10; 3/4 a viac.

Obrázok 3.- 1/4 a 1/2 sú ich vlastné zlomky. Zdroj: Wikimedia Commons.

Nevhodné zlomky

Čitateľ nesprávnych frakcií je väčší ako čitateľ. Napríklad 4/3, 8/5, 21/10 Patrí do tejto kategórie.

Zjavné zlomky

Tieto frakcie predstavujú celé číslo. Medzi nimi patrí 4/2, 10/5 a 27/3, pretože ak vyzeráme dobre, výsledok rozdelenia čitateľa medzi menovateľ týchto frakcií dáva celé číslo číslo.

Tak: 4/2 = 2, 10/5 = 2 a 27/3 = 9.

Rovnocenné frakcie

Dve frakcie N/M a P/Q sú ekvivalentné, keď sa delia čitateľ medzi menovateľom Rovnaké množstvo. Týmto spôsobom predstavujú rovnocenné frakcie rovnakú časť celku.

Ako príklad máme zlomky: 15/2 a 30/4. Rozdelením 15 x 2 dostanete 7.5, ale je to tiež rovnaké, ak je 30 rozdelených 4.

Môže vám slúžiť: Injektívna funkcia: z čoho pozostáva, na čo ide a príklady

Vedieť, či sú dve frakcie N/M a P/Q rovnocenné, je overená dodržiavanie nasledujúcej rovnosti:

N*q = m.p

Neredukovateľné zlomky

Keď sú čitateľ a menovateľ rozdelení tak istým číslom a pokiaľ je výsledok celý, získa sa frakcia ekvivalentná originálu, ale s menšími číslami.

Tento proces pokračuje, zatiaľ čo čitateľ a menovateľ majú rovnaký presný deliteľ. Ak nie je možné pokračovať v rozdelení, je to, že Neredukovateľný zlomok pôvodného zlomku.

Výhodou, ktorá musí pracovať s neredukovateľnou frakciou, je to, že sa získava ekvivalentná frakcia, ale s menším počtom. Preto, keď pracujete s zlomkami, musíte ich uľahčiť, aby ste ich uľahčili výpočty.

Predpokladajme, že frakcia 12/20, ktoré sú páry čitateľa a menovateľa, môžu byť rozdelené 2:

12/20 = 6/10

A ešte raz:

6/10 = 3/5

Frakcia 3/5 je rovnocenná s 12/20, ale jednoduchšia.

Zmiešané čísla

Nesprávna frakcia tiež pripúšťa reprezentáciu ako zmiešané číslo, ktoré sa nazýva tak, pretože má celú časť a ďalšiu zlomkovú časť, frakčná časť je zlomkom vlastnej časti.

Pozrime sa na rýchly príklad s zlomkom 15/2, o ktorom vieme, že je ekvivalentný 7.5.

Môžeme vyjadriť 15/2 ako zmiešané číslo, ako je toto:

15/2 = 7 + 0.5

Ale 0.5 = ½. Preto 15/2 = 7½, ktoré znie „sedem a médium“.

Príklady zlomkov

Frakčné čísla sú potrebné, pretože prírodné aj celé čísla sú nedostatočné, keď chceme rozdeliť veci ako čokoládová tyčinka.

Preto existuje nekonečná rozmanitosť meracích vzorov a objektov, ktorých špecifikácie zahŕňajú frakčné čísla, nehovoriac o množstve každodenných situácií, v ktorých sú potrebné.

Nákup potravín

V krajinách, v ktorých sa používa desatinný metrický systém, je používanie kilogramu bežné na označenie hmotnosti mnohých potravín. Nechceme vždy kupovať celé množstvá, ale o niečo viac alebo o niečo menej.

Preto sa pýtame:

• ½ kg rýb
• ¾ kg paradajok
• ¼ kilogram cibule
• 1 ½ kg broskýň (1 a pol kilogramu).

A keď používate vzorce merania anglo -Saxon, to isté sa stáva: potrebujeme 2 a pol libry alebo 1/4 niečoho.

Môže vám slúžiť: hodnotenie funkcií

Všetky tieto čísla sú frakčné a, ako sme videli, zodpovedajú dvom rôznym typom frakcií: vlastné a nesprávne.

Recepty

Recepty na kuchyňu často využívajú frakčné čísla na označenie počtu určitých zložiek. Napríklad:

• ½ šálky múky
• ¾ kg cukru na prípravu koláča.

Dĺžka a priemery

Rozmery nábytku, textilné kusy a všetky druhy domácich riadov sa merajú v frakciách metra alebo palca, či sa používa desatinný metrický systém opatrení alebo anglo -saxon.

Dokonca aj v krajinách, v ktorých prevláda desatinný metrický systém, komerčná meď, oceľ a iné inštalatérske materiály sa zvyčajne dodávajú s priemermi uvedenými v palcoch. Podobne aj iné hardvérové ​​kusy, ako sú skrutky a orechy.

Ako palec je rovnocenný s 2.54 cm, zvyčajne tieto kusy, ktoré majú menšie priemery, sú vyjadrené vo frakciách palca.

Veľmi časté opatrenia pre domáce rúry sú:

• ½ palca
• ¼ palca
• 3/8 a 5/8 palca.

Časové úseky

Denne sa frakčné čísla používajú na vyjadrenie časových intervalov, ako sú ¼, ½ a ¾ hodiny alebo dokonca o niečo väčšie: 1 hodina a ¼ atď.

Obrázok 4. Na týchto ručných hodinách sú polovica jedenástich. Zdroj: Pixabay.

Cvičenia s zlomkami

- Cvičenie 1

Dnes si Juanito vzal koláč do svojich narodenín do školy a chce ho distribuovať medzi všetkých svojich priateľov, ale učiteľ chce dať kus, ktorý je trikrát väčší, pokiaľ.

Berúc do úvahy, že existuje 24 detí + učiteľ, ktorému chce dať ekvivalent troch kusov, koľko kusov by mal koláč vyrezať?

Riešenie

Keby Juanito chcel distribuovať koláč iba medzi svojich priateľov, každý z nich by zodpovedal 1/24.

Ale ako chce učiteľ dať úlohu a že kus je trikrát väčší, musel by som distribuovať koláč medzi 24 študentmi + 3 kusmi pre učiteľa. To znamená, že každé dieťa zodpovedá 1/27 kusov a učiteľom 3/27 kusov.

Okrem toho, ak znížime frakciu 3/27, prinútime učiteľa, aby si vzal 1/9 časť koláča.

- Cvičenie 2

Spoločnosť s šéfom a traja zamestnanci majú každý mesiac príjmy vo výške 6 000 EUR. Koľko peňazí zodpovedá každá osoba, ak si šéf chce ponechať polovicu toho, čo vyhral?

Môže vám slúžiť: Rhomboid: Charakteristiky, ako vytiahnuť obvod a oblasť

Riešenie

Ak chce šéf vyhrať polovicu, musí zostať s 6000/2, čo robí 3000 EUR. Z ostatných zostávajúcich 3 000 EUR by mali byť distribuovaní traja zamestnanci. Každý zamestnanec teda vyhrá 3000/3, čo bude mať za následok 1 000 EUR.

- Cvičenie 3

Nájdite neredukovateľnú frakciu:

A) 12/18 a B) 4/11

Roztok

V prvom prípade sme si všimli, že čitateľ aj menovateľ sú rovnomerné a deliteľné medzi 2. Sú tiež deliteľné medzi 3, pretože 12 a 18 sú násobky tohto obrázku.

Takže môžeme frakciu zjednodušiť rozdelením čitateľa a menovateľa buď medzi 2 alebo 3, poradie je ľahostajné.

Počnúc rozdelením o 2:

12/18 = 6/9

Teraz si všimneme, že čitateľ aj menovateľ tejto ekvivalentnej frakcie sú násobky 3, a tak rozdeľujú obidva medzi týmto obrázkom:

6/9 = 2/3

A keďže 2 a 3 sú prvotné čísla, už nemajú žiadny iný spoločný deliteľ okrem 1. Dosiahli sme neredukovateľnú frakciu.

Maximálny spoločný deliteľ MCD čitateľa a menovateľa sa tiež mohol vypočítať. Pre 12 a 18:

MCD (12,18) = 6.

A potom je čitateľ a menovateľ rozdelený týmto číslom, čo je rovnocenné s tým v etapách.

Riešenie B

Tu si uvedomujeme, že 11 je hlavné číslo a jeho deliaci sú 1 a 11. Pokiaľ ide o svoju časť, 4 pripúšťa ako delení na 4, 2 a 1. S výnimkou 1, tieto čísla nemajú spoločného deliteľa, a preto je frakcia 4/11 neredukovateľná.

- Cvičenie 4

Uveďte, ktorý je najväčší zlomok každého páru:

a) ¾ a 5/4

b) 3/7 a 4/9

Roztok

Keď majú dva pozitívne frakcie toho istého menovateľa, najväčší je ten, ktorý má najväčšieho čitateľa. Preto je 5/4 väčší, od 5> 3.

Riešenie B

Ak frakcie N/M a P/Q majú iného menovateľa a obidve sú pozitívne, porovnávacie kritériá sú nasledujúce:

Bez.Q> m. P, potom n/m> p/q

Ďalšou možnosťou je nájsť desatinnú expresiu každej frakcie a porovnať.

Podľa prvého kritéria: n = 3, m = 7, p = 4, q = 9. Preto: n.Q = 3*4 = 12 a m.P = 7*4 = 28.

Ako 12< 28, ocurre que 3/7 < 4/9.

Alebo exprimujeme každú frakciu ako desatinné miesto a získame toto:

3/7 = 0.428571428… .

4/9 = 0.44444444… .

Podporné body naznačujú, že množstvo desatinných miest je nekonečné. Ale to stačí na overenie, že skutočne 4/9> 3/7.

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Carena, m. 2019. Matematická príručka. Národná univerzita pobrežia.
3. Figuera, J. 2000. Matematika 8. Edície Co-Bo.
4. Jiménez, r. 2008. Algebra. Sála.
5. Stránka matematiky. Čo je to zlomok? Získané z: ThemathPage.com.