Inferenciálna história štatistík, charakteristiky, na čo ide, príklady

Ten Inferenčné štatistiky alebo deduktívna štatistika je taká, ktorá odpočíta charakteristiky populácie zo vzoriek extrahovaných z nej prostredníctvom série analytických techník. Pri získaných informáciách sú modely rozpracované, ktoré potom umožňujú predpovede o správaní uvedenej populácie.

Preto sa inferenčné štatistiky stali vedou číslo jedna, ktorá ponúka výživu a nástroje, ktoré pri rozhodovaní vyžadujú nespočetné disciplíny.

Fyzika, chémia, biológia, inžinierstvo a spoločenské vedy, z týchto nástrojov neustále ťaží, keď vytvárajú svoje modely a navrhujú a implementujú experimenty.

[TOC]

Stručná história inferenciálnych štatistík

Štatistiky vznikli v staroveku kvôli potrebe ľudí organizovať veci a optimalizovať zdroje. Pred vynálezom písania sa uskutočňovali záznamy o počte ľudí a hospodárskych zväzkoch prostredníctvom symbolov, ktoré boli zaznamenané v kameni.

Neskôr čínštiny, babylonskí a egyptskí vládcovia zanechali údaje o množstve plodín a počtu obyvateľov zaznamenaných na tabletoch, stĺpcoch a pamiatkach.

Rímska ríša

Keď Rím uplatnil svoju doménu v Stredomorí, bolo bežné, že úrady vykonávajú sčítanie ľudu každých päť rokov. V skutočnosti slovo „štatistické“ pochádza z talianskeho slova štatista, Čo to znamená vyjadriť.

Súbežne, v Amerike priniesli podobné záznamy aj veľké predpriesky.

Stredovek

Počas stredoveku vlády Európy, ako aj cirkev, zaregistrovali majetok Zeme. Potom urobili to isté s narodením, krstmi, manželstvami a úmrtiami.

Moderný vek

Anglická štatistika John Graunt (1620-1674) bola prvá, ktorá predpovedala predpovede na základe týchto zoznamov, ako napríklad koľko ľudí môže zomrieť na určité choroby a odhadovaný podiel narodenia žien a mužov. Preto sa považuje za otca demografie.

Súčasný vek

Neskôr, s príchodom teórie pravdepodobností, štatistika prestala byť iba zbierkou organizačných techník a dosiahla netušený rozsah ako prediktívnu vedu.

Preto boli odborníci schopní.

Charakteristika

Ďalej máme najrelevantnejšie charakteristiky tejto odvetvia štatistík:

- Inferenciálna štatistika študuje populáciu, ktorá z nej berie reprezentatívnu vzorku.

- Výber vzorky sa vykonáva rôznymi postupmi, pričom najvhodnejšie sú tí, ktorí si komponenty náhodne vyberajú. Aký.

Môže vám slúžiť: Ako previesť z km/h a m/s? Vyriešené cvičenia

- Na zorganizovanie zhromaždených informácií využíva opisné štatistiky.

- Na vzorke sa vypočítajú štatistické premenné, ktoré slúžia na odhad vlastností populácie.

- Inferenčné alebo deduktívne štatistiky využívajú teóriu pravdepodobností na štúdium náhodných udalostí, tj tie, ktoré vznikajú náhodne. Každej udalosti je pridelená určitá pravdepodobnosť výskytu.

- Zostavte hypotézy - supositions - o parametroch populácie a kontrastujte ich, aby ste vedeli, či sú alebo nie sú správne, a tiež vypočíta úroveň dôvery reakcie, to znamená, že ponúka maržu chyby. Prvý postup sa volá testy hypotézy, Zatiaľ čo marža chyby je interval spoľahlivosti.

Čo je opisná štatistika pre? Žiadosti

Inferenčné štatistiky: nevyhnutné pri rozhodovaní a kontrole kvality

Štúdium v ​​celom rozsahu by populácia mohla požadovať veľa zdrojov v peniazoch, čase a úsilí. Je lepšie odobrať reprezentatívne vzorky, ktoré sú oveľa zvládnuteľnejšie, zhromažďujú údaje prostredníctvom nich a vytvárajú hypotézy alebo predpoklady o správaní vzorky.

Akonáhle sú hypotézy stanovené a ich platnosť je porovnaná, výsledky sa rozširujú na populáciu a používajú sa na rozhodovanie.

Pomáhajú tiež vytvárať modely tejto populácie, robiť budúce projekcie. Preto je inferenciálna štatistika veľmi užitočnou vedou pre:

Sociológia a demografické štúdie

Jedná sa o ideálne aplikačné oblasti, pretože štatistické techniky sa vzťahujú s myšlienkou vytvorenia rôznych modelov ľudského správania. Niečo, čo a priori je dosť komplikované, pretože početné premenné zasahujú.

V politike sa vo volieb používa veľa na poznanie tendencie voličov, týmto spôsobom, stratégie navrhovania strán strany.

Inžinierstvo

Inferenčné štatistické metódy sa široko používajú v inžinierstve, najdôležitejšie aplikácie sú regulácia kvality a optimalizácia procesov, napríklad zlepšovanie časov pri vykonávaní úloh, ako aj pri prevencii pracovných nehôd.

Hospodárstvo a podniková správa 

S deduktívnymi metódami sa môžu projekcie vykonávať o prevádzke spoločnosti, očakávanej úrovni predaja a pomoci pri rozhodovaní.

Napríklad vaše techniky môžu byť použité na odhad reakcie kupujúcich na nový produkt, blízko k spusteniu na trhu.

Slúži tiež na vyhodnotenie toho, čo sú modifikácie v spotrebiteľských návykoch ľudí, vzhľadom na dôležité udalosti, ako napríklad covidná epidémia.

Príklady inferenciálnych štatistík

Príklad 1

Jednoduchý deduktívny štatistický problém je nasledujúci: Učiteľ matematiky má na starosti 5 sekcií základnej algebry na univerzite a rozhodne sa použiť priemerné poznámky jednej zo svojich sekcií na odhad priemeru všetkých všetkých.

Môže vám slúžiť: približné meranie amorfných figúr: Príklad a cvičenieAvšak veľká populácia je možné študovať prostredníctvom reprezentatívnej vzorky. Zdroj: Pixabay.

Ďalšou možnosťou je odobrať vzorku každej sekcie, študovať jej charakteristiky a rozšíriť výsledky na všetky oddiely.

Príklad 2

Manažér obchodu s odevmi pre dámy chce vedieť, koľko sa v letnej sezóne predá určitá blúzka. Aby sme to dosiahli, analyzujte predaj odevov počas prvých dvoch týždňov sezóny, a preto určte tento trend.

Základné pojmy v inferenciálnej štatistike

Existuje niekoľko kľúčových konceptov, vrátane tých, ktoré pochádzajú z teórie pravdepodobností, čo je potrebné, aby sme pochopili všetky rozsahy týchto techník. Niektorí, ako populácia a vzorka, sme už v texte spomínali.

Udalosť

Udalosť alebo udalosť je niečo, čo sa stane, a to môže mať niekoľko výsledkov. Príkladom udalosti môže byť spustenie meny a existujú dva možné výsledky: tvár alebo tesnenie.

Vzorový priestor

Je to sada všetkých možných výsledkov udalosti.

Populácia a vzorka

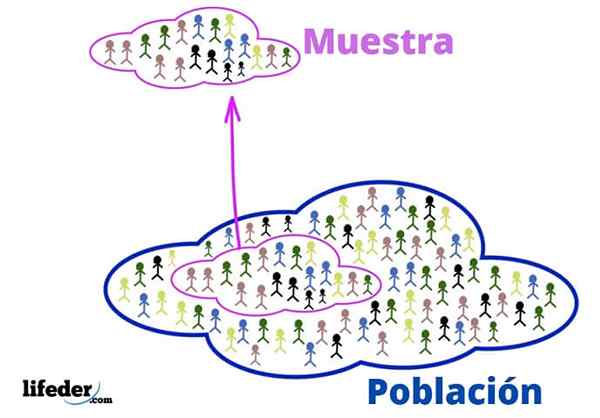Populácia a vzorka

Populácia je vesmír na štúdium. Nie sú nevyhnutne o žijúcich ľuďoch alebo bytostiach, pretože populácia v štatistike môže pozostávať z objektov alebo nápadov.

Vzorka je podmnožinou populácie, ktorá je z nej starostlivo extrahovaná za to, že je reprezentatívna.

Vzorkovanie

Je to súbor techník, prostredníctvom ktorých je vzorka vybraná z danej populácie. Odber vzoriek môže byť náhodný, ak sa pravdepodobné metódy použijú na výber vzorky alebo nie pravdepodobné, ak má analytik vlastné kritérium výberu podľa svojich skúseností.

Štatistické premenné

Sada hodnôt, ktoré môžu mať charakteristiky populácie. Sú klasifikované niekoľkými spôsobmi, napríklad môžu byť diskrétne alebo nepretržité. Podľa svojej povahy môžu byť tiež kvalitatívne alebo kvantitatívne.

Distribúcia pravdepodobnosti

Pravdepodobné funkcie opisujúce správanie veľkého počtu systémov a situácií pozorovaných v prírode. Najznámejšie sú gaussovské distribúcie alebo Gauss Bell a Binomial Distribution.

Parametre a štatistika 

Teória odhadu uvádza, že existuje vzťah medzi hodnotami populácie a hodnotami vzorky odobratej z tejto populácie. Ten parametre Sú to charakteristiky populácie, ktoré nevieme, ale chceme odhadnúť: napríklad priemer a štandardná odchýlka.

Po jeho časti štatistický sú charakteristiky vzorky, napríklad jej priemerná a štandardná odchýlka.

Predpokladajme, že populácia pozostáva zo všetkých mladých ľudí medzi 17 a 30 rokmi komunity a je potrebné poznať podiel osôb v súčasnosti vo vysokoškolskom vzdelávaní. Toto by bol stanovený parameter populácie.

Môže vám slúžiť: lineárna interpolácia

Na to sa vyberie náhodná vzorka 50 mladých ľudí a vypočíta sa ich podiel, ktorý študuje na univerzite alebo inštitúte vysokoškolského vzdelávania. Tento podiel je štatistika.

Ak sa štúdia vykonáva, zistilo sa, že 63 % z 50 mladých ľudí študuje vyššie, je to odhadovaná populácia, vyrobená zo vzorky.

Toto je len príklad toho, čo môže inferenciálna štatistika urobiť. Je známy ako odhad, ale existujú aj techniky na predpovedanie štatistických premenných, ako aj na rozhodovanie.

Štatistická hypotéza

Je to domnienka, ktorá sa vytvára v súvislosti s hodnotou priemeru a štandardnej odchýlky niektorých charakteristík populácie. Pokiaľ nie je populácia úplne vyšetrená, sú to neznáme hodnoty.

Testy hypotézy

Sú predpoklady, ktoré sa týkajú platných parametrov populácie? Ak to chcete poznať, overuje sa, či ich výsledky zo vzorky podporujú alebo nie, preto je potrebné navrhnúť testy hypotéz.

Toto sú všeobecné kroky na vykonanie jedného:

Krok 1

Identifikujte typ distribúcie, ktorý sa očakáva, že bude nasledovať populácia.

Krok 2

Zvýšte dve hypotézy označené ako h_ani a h₁. Prvým je nulová hypotéza v ktorom predpokladáme, že parameter má určitú hodnotu. Druhý je Alternatívna hypotéza čo je iná hodnota ako nulová hypotéza. Ak je to zamietnuté, akceptuje sa alternatívna hypotéza.

Krok 3

Stanovte prijateľnú maržu pre rozdiel medzi parametrom a štatistikou. Budú zriedka identické, hoci sa očakáva, že budú veľmi blízko.

Krok 4

Navrhnite kritérium na prijatie alebo odmietnutie nulovej hypotézy. Na tento účel sa používa štatistika testu, ktorá môže byť priemerná. Ak je priemerná hodnota v rámci určitých limitov, akceptuje sa nulová hypotéza, inak je odmietnutá.

Krok 5

Ako posledný krok sa rozhoduje, či je nulová hypotéza akceptovaná alebo nie.

Záujmové témy

Štatistické vety.

Štatistické premenné.

Populácia a vzorka.

Deskriptívna štatistika.

Odkazy

1. Berenson, m. 1985.Štatistiky pre správu a hospodárstvo, koncepty a aplikácie. Inter -American Editorial.
2. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
3. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Učenie sa.
4. Štatistika. Získané z: eumed.slepo.
5. Ibañez, P. 2010. Matematika II. Prístup. Učenie sa.
6. Levin, r. 1981. Štatistiky pre administrátorov. Sála.
7. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.