História opisnej štatistiky, charakteristiky, príklady, koncepty

Ten Deskriptívna štatistika Je to odvetvie štatistík, ktorá sa zaoberá zhromažďovaním a organizovaním informácií o správaní systémov s mnohými prvkami, všeobecne známymi ako názov populácia.

Na tento účel používa numerické a grafické techniky, prostredníctvom ktorých predstavuje informácie, bez predpovedí alebo záverov o populácii, v ktorej prichádza.

Opisná štatistika sa považuje za usporiadanie a prezentáciu informácií

[TOC]

História

Staroba

Štatistika má svoj pôvod v ľudskej potrebe zorganizovať potrebné informácie pre jeho prežitie a dobre, ako aj zabezpečiť udalosti, ktoré ich ovplyvňujú. Veľké civilizácie staroveku ponechali záznamy osadníkov, vyberané dane, množstvo plodín a veľkosť armád.

Napríklad počas jeho dlhej vlády, Ramses II (1279-1213 až.C) nariadil sčítanie pôdy a obyvateľov v Egypte, ktoré vtedy malo asi 2 milióny obyvateľov.

Podobne aj Biblia, ktorú Mojžiš vykonal sčítanie ľudu, aby vedel, koľko vojakov malo dvanásť kmeňov Izraela.

Aj v starovekom Grécku boli vyrobené ľudí a zdroje. Rimania, pozoruhodní pre svoju vysokú organizáciu, pravidelne zaregistrovali populáciu a pripravovali sčítanie ľudu každých päť rokov vrátane území a zdrojov.

Renesancia

Po úpadku Ríma sa dôležité štatistické záznamy vystrašili až do príchodu renesancie, keď sa štatistika znovu objaví.

Vyvrcholenie sedemnásteho storočia, zrodila sa teória pravdepodobností, výsledok sklonu ľudí k hazardom, ktorý poskytol štatistiku matematickú prísnosť, ktorá z nej urobila vedu samostatne.

Moderný vek

Nový impulz prišiel s teóriou chýb a minimálnymi štvorcami v devätnástom storočí, ktoré nasledovali metódu korelácie medzi premennými, aby kvantitatívne vyhodnotili vzťah medzi nimi.

Až konečne, počas dvadsiateho storočia, štatistika rozšírila na každú odvetvie vedy a inžinierstva ako nevyhnutný nástroj pri riešení problémov.

Charakteristiky popisných štatistík

Opisná štatistika sa vyznačuje:

- Zorganizujte informácie zozbierané v údajoch a grafiku. Grafy môžu byť rozmanité: histogramy, frekvenčné polygóny, koláčové diagramy, okrem iného.

- Distribuovať údaje vo frekvenčných rozsahoch, aby sa uľahčilo ich riadenie. Použite aritmetiku na nájdenie najreprezentatívnejších hodnôt údajov, prostredníctvom miery centrálnej tendencie, ako aj ich analyzujte ich rozptýlenie.

- Určite tvar distribúcie, ich symetriu, ak sú centrované alebo zaujaté, a ak sú špicaté alebo skôr sploštené.

Môže vám slúžiť: Implicitné deriváty: Ako sú vyriešené a vyriešené cvičenia

Čo je opisná štatistika pre?

Kedykoľvek je to potrebné.

Potom spomenieme niekoľko príkladov:

Hospodárnosť

Opisná štatistika sa zaoberá registráciou a organizovaním údajov o populáciách a ich veku, príjmoch, investíciách, zisku a výdavkoch. Týmto spôsobom vlády a inštitúcie plánujú vylepšenia a primerane investujú.

S vašou pomocou vám monitoruje nákupy, predaj, výnosy a efektívnosť služieb. Z tohto dôvodu sú štatistiky nevyhnutné pri rozhodovaní.

Fyzika a mechanické

Fyzika a mechanika používajú štatistiku na štúdium kontinuálneho média, ktoré pozostávajú z veľkého počtu častíc, ako sú atómy a molekuly. Ukazuje sa, že nie je možné každú z nich monitorovať osobitne.

Ale štúdium globálneho správania systému (napríklad plynnej časti) z makroskopického hľadiska je možné zistiť priemery a definovať makroskopické premenné, aby ste poznali jeho vlastnosti. Príkladom je kinetická teória plynov.

Liek

Je to nevyhnutný nástroj pri monitorovaní chorôb, z jeho pôvodu a počas jeho vývoja, ako aj z účinnosti liečby.

Štatistiky, ktoré opisujú mieru morbidity, hojenia, časov inkubácie alebo vývoja choroby, vek, v ktorom sa zvyčajne objavuje, a údaje o štýle, sú potrebné pri navrhovaní najúčinnejších ošetrení.

Výživa

Jednou z mnohých aplikácií popisných štatistík je registrácia a objednávanie údajov o spotrebe potravín v rôznych populáciách: ich kvantita, kvalita a ktoré sú najviac konzumované, medzi mnohými ďalšími pozorovaniami, ktoré záujmové odborníci.

Príklady opisných štatistík

Ďalej uvidíme niekoľko príkladov, ktoré ilustrujú, aké užitočné sú nástroje opisných štatistík na pomoc pri rozhodovaní:

Príklad 1

Na zlepšenie školských jedál sa vyžadujú informácie o používateľoch. Zdroj: Wikimedia Commons.

Vzdelávacie orgány krajiny plánujú inštitucionálne zlepšenia. Predpokladajme, že implementujú nový systém školských jedál.

Z tohto. Potom sú tieto informácie uvedené vo forme tabuliek a grafov.

Príklad 2

Na sledovanie miestneho futbalového tímu a vytvorenie nových podpisov, manažéri nesú počet hraných zápasov, vyhraných, zviazaných a stratených, ako aj počet gólov, strelcov a spôsobu, akým sa im podarilo skórovať: voľný kop z polovice súdu, pokuty, s ľavou nohou alebo vpravo, okrem iného.

Môže vám slúžiť: vzájomne sa vylučujú udalosti: Vlastnosti a príklady

Príklad 3

Obchod so zmrzlinou má niekoľko príchutí zmrzliny a chce zlepšiť svoj predaj, preto majitelia vykonávajú štúdiu, v ktorej počítajú počet zákazníkov, rozdeľujú ich do skupín podľa pohlavia a vekového rozpätia.

V tejto štúdii sa zaznamenáva napríklad obľúbená chuť zmrzliny a najpredávanejšia prezentácia. A so zhromaždenými údajmi plánujú nákupy chutí a potrebné kontajnery a príslušenstvo na ich prípravu.

Základné pojmy popisných štatistík

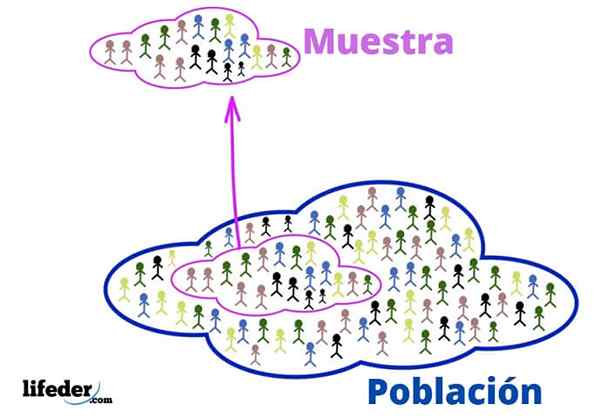Populácia a vzorka

Tieto základné koncepty sú potrebné na uplatňovanie štatistických techník, pozrime sa:

Populácia

V štatistickom kontexte sa populácia týka vesmíru alebo kolektívu, z ktorého informácie pochádzajú.

Nie je to vždy o ľuďoch, pretože to môžu byť súpravy zvierat, rastlín alebo predmetov, ako sú autá, atómy, molekuly a dokonca aj udalosti a nápady.

Vzorka

Ak je populácia veľmi veľká, z nej sa extrahuje reprezentatívna vzorka a analyzuje sa bez straty relevantných informácií.

Môže byť vybraný náhodne alebo podľa niektorých kritérií, ktoré predtým stanovil analytik. Výhodou je, že byť podskupinou populácie, je oveľa zvládnuteľnejšia.

Variabilný

Vzťahuje sa na súbor hodnôt, ktoré môžu mať určitú charakteristiku populácie. Štúdia môže obsahovať rôzne premenné, ako napríklad vek, pohlavie, hmotnosť, akademická úroveň, občiansky stav, príjem, teplota, farba, čas a mnoho ďalších.

Premenné môžu mať inú povahu, takže existujú kritériá na ich klasifikáciu a poskytnutie najvhodnejšej liečby.

Kategorické premenné a numerické premenné

Podľa spôsobu, akým sa merajú, môžu byť premenné:

-Kategorický

-Číselný

Kategorické premenné, ktoré sa tiež nazývajú kvalitatívny, Predstavujú vlastnosti, ako je občianske postavenie osoby, ktorá môže byť slobodná, ženatá, rozvedená alebo vdova.

Na druhej strane, numerické premenné alebo kvantitatívny, Môžu sa merať, napríklad vek, čas, hmotnosť, príjem a ďalšie.

Grafika je veľmi dôležitá na prezentáciu informácií, pretože na prvý pohľad sa ocenia trend údajov. Zdroj: piqsels.

Diskrétne a kontinuálne premenné premenné

Diskrétne premenné berú iba diskrétne hodnoty, ako názov napovedá. Príkladmi z nich je počet detí rodiny, koľko predmetov je v určitom kurze a množstvo automobilov na parkovisku.

Tieto premenné nie vždy berú celé hodnoty, pretože existujú aj frakcionári.

Na druhej strane nepretržité premenné pripúšťajú nekonečné hodnoty v určitom rozsahu, ako napríklad hmotnosť osoby, pH krvi, čas telefonickej konzultácie a priemer futbalových loptičiek.

Môže vám slúžiť: symetria

Opatrenia centrálnej tendencie

Určite všeobecný trend, ktorý nasledujú údaje. Uveríme tri najpoužívanejšie centrálne opatrenia:

-Polovica

-Stredný

-Formovať

Polovica

Rovnocenné s priemernými hodnotami. Vypočíta sa pridaním všetkých pozorovaní a rozdelením medzi celkový počet:

 Kde x_Jo Je to akékoľvek pozorovanie a n je ich celkom.

Formovať

Je to hodnota, ktorá sa najviac opakuje v súbore údajov, najčastejšie, pretože v distribúcii môže byť viac ako jedna móda.

Stredný

Pri objednávaní súboru údajov je medián ústrednou hodnotou všetkých z nich.

Opatrenia

Poukazujú na variabilitu údajov a poskytujú predstavu o tom, ako ďaleko alebo rozptýlené sú z ústredných opatrení. Najpoužívanejšie sú:

Rozsah

Je to rozdiel medzi najväčšou hodnotou x_M a najmenší x_m súboru údajov:

Rozsah = x_M - X_m

Rozptyl

Zmerajte, ako ďaleko sú údaje priemernej hodnoty. Z tohto_Jo a priemer, štvorcový, aby sa zabránilo tomu, aby sa navzájom rušili. Zvyčajne sa označuje gréckym písmenom σ štvorcovým alebo s S²:

Štandardná odchýlka

Rozptyl nemá rovnaké jednotky ako údaje, takže štandardná odchýlka je definovaná ako druhá druhá koreň rozptylu a označuje sa ako σ alebo S:

Frekvenčné rozdelenie

Namiesto toho, aby ste zohľadnili jednotlivé údaje individuálne, je vhodnejšie ich zoskupiť do rozsahov, čo uľahčuje prácu, najmä ak existuje veľa hodnôt. Napríklad pri práci s deťmi školy môžu byť zoskupené do vekových rozsaží: od 0 do 6 rokov, od 6 do 12 rokov a od 12 do 18 rokov.

Grafy

Predstavujú vynikajúci spôsob, ako oceniť distribúciu údajov z pohľadu a obsahovať všetky informácie zhromaždené v tabuľkách a obrázkoch, ale oveľa dostupnejšie.

Existuje ich široká škála: s tyčami, lineárnymi, kruhovými, stonkami a listmi, histogramami, frekvenčnými polygónmi a piktogramami. Príklady štatistických grafov sú uvedené na obrázku 3.

Záujmové témy

Štatistické vety.

Štatistické premenné.

Populácia a vzorka.

Inferenčné štatistiky.

Odkazy

1. Faraldo, P. Štatistika a metodika výskumu. Získané z: eio.USC.je.
2. Fernández, s. 2002. Deskriptívna štatistika. Druhý. Vydanie. Redakcia. Obnovené z: knihy Google.
3. Štatistika. Získané z: eumed.slepo.
4. Ibañez, P. 2010. Matematika II. Prístup. Učenie sa.
5. Monroy, s. 2008. Deskriptívna štatistika. 1. Vydanie. Národný polytechnický inštitút v Mexiku.
6. Vesmír. Deskriptívna štatistika. Získané z: Universoformulas.com.