Matematika

Vzorky vzorkovania chybových vzorcov a rovníc, výpočet, príklady

Vzorky vzorkovania chybových vzorcov a rovníc, výpočet, príklady

On chyba vzorkovania ani chyba vzorky V štatistike je to rozdiel medzi priemernou hodnotou vzorky vzhľadom na priemernú hodnotu celkovej populácie. Na ilustráciu tejto myšlienky si predstavme, že celková populácia mesta je jeden milión, z ktorých chcete jeho priemerné topánky, pre ktoré sa tisíc ľudí odoberá náhodnou vzorkou.

Priemerná veľkosť vyplývajúca zo vzorky sa nemusí nevyhnutne zhodovať s veľkosťou celkovej populácie, hoci ak nie je vzorka zaujatá, hodnota musí byť blízko. Tento rozdiel medzi priemernou hodnotou vzorky a hodnotou celkovej populácie je chyba vzorky.

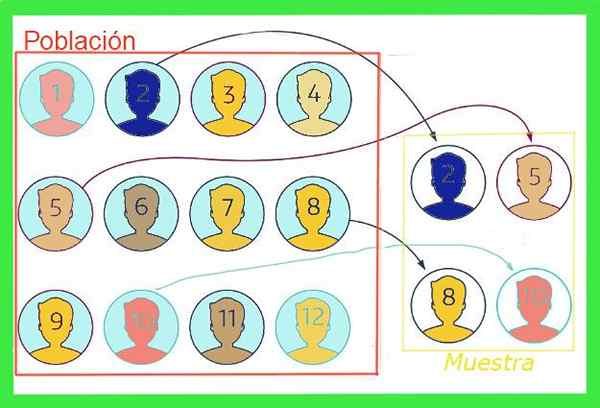
postava 1. Pretože vzorka je podskupinou celkovej populácie, priemer vzorky má maržu chyby. Zdroj: f. Zapata.

Všeobecne platí, že priemerná hodnota celkovej populácie nie je známa, ale existujú techniky na zníženie takýchto chýb a vzorcov na odhad Ukážka chyby ktoré budú vystavené v tomto článku.

[TOC]

Vzorce a rovnice

V prípade, že chcete poznať priemernú hodnotu určitej merateľnej funkcie X V populácii veľkosti N, ale ako N Je to veľké množstvo nie je životaschopné študovať celkovú populáciu, a preto pokračujeme v a rozbaľovacia vzorka veľkosť n<.

Priemerná hodnota vzorky je označená a priemerná hodnota celkovej populácie ju označuje za grécky list μ (znie to Mu alebo miu).

Predpokladajme, že sú vzaté m Celkové vzorky populácie N, Celá rovnaká veľkosť n S priemernými hodnotami 1>, 2>, 3>, .. .m>.

Tieto priemerné hodnoty nebudú navzájom totožné a všetky budú okolo priemernej hodnoty populácie μ. On Vzorová chyba marža e označuje očakávané oddelenie priemerných hodnôt vzhľadom na Priemerná hodnota populácie μ v rámci stanoveného percentuálneho podielu nazývaného Úroveň dôvery γ (Gamma).

Môže vám slúžiť: aditívna inverzia

On Štandardná chyba vzorky veľkosti n je:

ε = σ/√n

kde σ je štandardná odchýlka (Druhá koreň rozptylu), ktorá sa vypočíta podľa nasledujúceho vzorca:

σ = √ [(x -)2/(N - 1)]

Význam Štandardná chyba je nasledujúci:

On stredná hodnota získané vzorkou veľkosti n sa v intervale chápe ( - ε, + ε) s úroveň sebavedomia 68,3%.

Ako vypočítať chybu vzorkovania

V predchádzajúcej časti bol uvedený vzorec na nájdenie rozsah chýb norma vzorky n, kde štandardné slovo naznačuje, že ide o maržu chyby so 68% dôverou.

To naznačuje, že ak sa odobralo veľa vzoriek rovnakej veľkosti n, 68% z nich poskytne priemerné hodnoty v rozsahu [ - ε, + ε].

Existuje jednoduché pravidlo, nazývané Pravidlo 68-95-99.7 To nám umožňuje nájsť okraj Vzorová chyba e Pre úroveň dôvery 68%, 95% a 99,7% Ľahko, pretože táto marža je 1ypε, 2 šuε a 3 šuε respektíve.

Pre úroveň dôvery γ

Ak on Úroveň dôvery γ Nie je to nič z vyššie uvedeného, ​​takže chyba odberu vzoriek je štandardná odchýlka σ vynásobené faktorom Zy, ktorý sa získava nasledujúcim postupom:

1.- Najskôr úroveň významnosti α ktorý sa vypočíta z Úroveň dôvery γ Prostredníctvom nasledujúceho vzťahu: α = 1 - γ

Môže vám slúžiť: Bayesova veta

2.- Potom musíte vypočítať hodnotu 1 - a/2 = (1 + γ)/2, čo zodpovedá normálnej frekvencii akumulovanej medzi -∞ a Zy, V normálnom alebo gaussovskom rozdelení typom F (z), ktorého definíciu je vidieť na obrázku 2.

3.- Rovnica je vyriešená F (z y) = 1 - a/2 Cez normálne distribučné tabuľky (akumulované) F, o prostredníctvom počítačovej aplikácie, ktorá má typizovanú inverznú gaussovskú funkciu F-1.

V druhom prípade máte:

Zy = g-1(1 - a/2).

4.- Nakoniec sa použije tento vzorec pre chybu vzorkovania s úrovňou spoľahlivosti γ:

E = zy⋅(σ/√n)

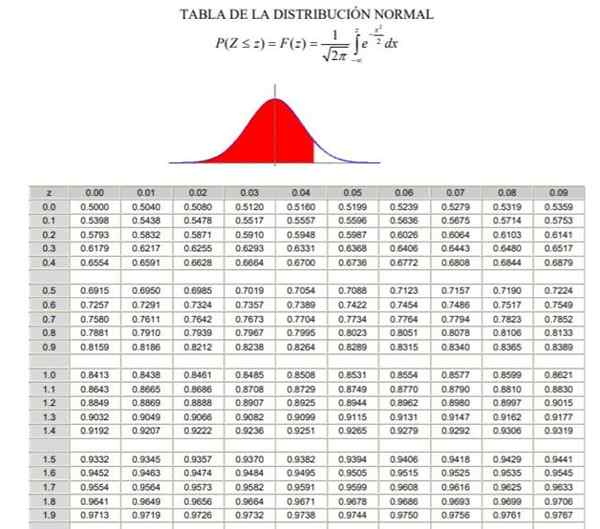Obrázok 2. Tabuľka normálnej distribúcie. Zdroj: Wikimedia Commons.

Príklady

- Príklad 1

Vypočítať Štandardná chyba O priemernej hmotnosti vzorky 100 novorodencov. Výpočet priemernej hmotnosti bol = 3 100 kg so štandardnou odchýlkou σ = 1 500 kg.

Riešenie

On Štandardná chyba je ε = σ/√n = (1 500 kg)/√100 = 0,15 kg. Čo znamená, že pri týchto údajoch možno odvodiť, že hmotnosť 68% novorodencov je medzi 2 950 kg a 3.25 kg.

- Príklad 2

Určiť okraj chyby vzorky a a rozsah hmotnosti 100 novorodencov s 95% úrovňou spoľahlivosti, ak je priemerná hmotnosť 3 100 kg so štandardnou odchýlkou σ = 1 500 kg.

Riešenie

Ak Pravidlo 68; 95; 99.7 → 1lekε; 2 šuε; 3 šuε, Máš:

E = 2 šcek

Inými slovami, 95% novorodencov bude mať pesos medzi 2 800 kg a 3 400 kg.

- Príklad 3

Určite rozsah pesos novorodencov v príklade 1 s 99,7% maržou dôveryhodnosti.

Môže vám slúžiť: Rhomboid: Charakteristiky, ako vytiahnuť obvod a oblasť

Riešenie

Chyba vzorky s 99,7% dôverou je 3 σ/√n, To je pre náš príklad E = 3 *0,15 kg = 0,45 kg. Odtiaľ sa usudzuje, že 99,7% novorodencov bude mať pesos medzi 2 650 kg a 3 550 kg.

- Príklad 4

Určiť faktor Zy Pre úroveň spoľahlivosti 75%. Určite maržu chyby odberu vzoriek s touto úrovňou spoľahlivosti pre prípad zvýšeného v príklade 1.

Riešenie

On úroveň sebavedomia je γ = 75% = 0,75, ktoré sa týka významnosť α prostredníctvom vzťahu γ= (1 - α), takže úroveň významnosti je α = 1 - 0,75 = 0,25.

To znamená, že akumulovaná normálna pravdepodobnosť medzi -∞ a Zy je:

P (z ≤ Zy ) = 1 - 0,125 = 0,875

Čo zodpovedá hodnote Zy 1 1503, ako je znázornené na obrázku 3.

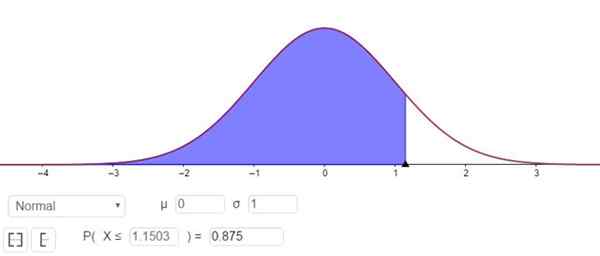Obrázok 3. Stanovenie faktora ZY zodpovedajúceho 75% úrovne spoľahlivosti. Zdroj: f. Zapata cez geogebra.

Inými slovami, chyba odberu vzoriek je E = zy⋅(σ/√n)= 1.15⋅(σ/√n).

Ak sa uplatňuje na príklad 1 údajov, poskytne chybu:

E = 1,15*0,15 kg = 0,17 kg

S úrovňou spoľahlivosti 75%.

- Cvičenie 5

Aká je úroveň dôvery, ak zα/2 = 2.4 ?

Riešenie

P (z ≤ zα/2 ) = 1 - a/2

P (z ≤ 2.4) = 1 - a/2 = 0,9918 → a/2 = 1 - 0,9918 = 0,0082 → a = 0,0164

Úroveň významnosti je:

a = 0,0164 = 1,64%

A nakoniec, úroveň dôvery zostáva:

1- a = 1 - 0,0164 = 100% - 1,64% = 98,36%

Odkazy

  1. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
  2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
  3. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
  4. Sudman, s.1982. Kladenie otázok: Praktický sprievodca dizajnom dotazníka. San Francisco. Jossey bas.
  5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.
  6. Wonnacott, t.H. a r.J. Vyhraba. 1990. Úvodná štatistika. 5. vydanie. Mravný
  7. Wikipedia. Chyba vzorky. Zdroj: In.Wikipedia.com
  8. Wikipedia. Marža chyby. Zdroj: In.Wikipedia.com