U -test z Mann - Whitney Čo je a kedy sa uplatňuje, vykonanie, príklad

Ten U -test Mann - Whitney Používa sa na porovnanie dvoch nezávislých vzoriek, keď majú málo údajov alebo nedodržiavajú normálnu distribúciu. Týmto spôsobom sa to považuje za test nie parametrický, Na rozdiel od vášho náprotivku Študent T Test, Používa sa, keď je vzorka dostatočne veľká a sledujte normálne rozdelenie.

Frank Wilcoxon to navrhuje prvýkrát v roku 1945, pre vzorky rovnakých veľkostí, ale o dva roky neskôr sa predĺžil v prípade vzoriek inej veľkosti Henryho Mann a D. R. Whitney.

postava 1. U -test Mann - Whitney sa používa na porovnanie nezávislých vzoriek. Zdroj: Pixabay.

Test sa často používa na overenie, či existuje vzťah medzi kvalitatívnou premennou a inou kvantitatívnou.

Ilustratívnym príkladom je vziať súbor hypertenzných ľudí a extrahovať dve skupiny, ktorým sa denné údaje o krvnom tlaku zaznamenávajú mesiac.

Do jednej skupiny liečba A a druhá sa aplikuje liečba B. Tu je krvný tlak kvantitatívna premenná a typ liečby je kvalitatívny.

Chcete vedieť, či je medián, a nie priemer, nameraných hodnôt štatisticky rovnocenné alebo odlišné, aby ste zistili, či existuje rozdiel medzi oboma ošetreniami. Na získanie odpovede sa aplikuje Wilcoxon alebo U -Test of Mann - Whitney.

[TOC]

Problémový prístup v U -teste Mann - Whitney

Ďalším príkladom, v ktorom je možné test uplatniť, je nasledujúci:

Predpokladajme, že chcete vedieť, či sa konzumácia nealkoholických nápojov výrazne líši v dvoch regiónoch krajiny.

Jeden z nich sa nazýva región A a druhý región B. Rekordný liter konzumovaný týždenne v dvoch vzorkách sa vykonáva: jeden z 10 ľudí pre región A a druhý z 5 ľudí pre región B.

Údaje sú nasledujúce:

-Región a: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Región B: 12,14, 11, 30, 10

Vyvolá sa nasledujúca otázka:

Závisí konzumácia nealkoholických nápojov (y) od oblasti (x)?

Kvalitatívne premenné verzus kvantitatívne premenné

-Kvalitatívna premenná x: Región

-Kvantitatívna premenná a: Plynná spotreba

Ak je množstvo spotrebovaných litrov rovnaké v oboch regiónoch, záver bude, že medzi týmito dvoma premennými nie je závislosť. Spôsob, ako to vedieť, je porovnanie priemerného alebo stredného trendu pre tieto dva regióny.

Normálny prípad

Ak údaje sledovali normálne rozdelenie, zvýši sa dve hypotézy: null H0 a alternatíva H1 porovnaním medzi prostriedkami:

Môže vám slúžiť: pozoruhodné výrobky

-H0: Neexistuje žiadny rozdiel medzi priemerom týchto dvoch regiónov.

-H1: Prostriedky oboch regiónov sú rôzne.

Prípad bez - normálnej tendencie

Naopak, ak údaje nedodržiavajú normálne rozdelenie alebo jednoducho vzorka je veľmi malá, namiesto porovnania priemeru, ktorý by sa porovnal Stredný z dvoch regiónov.

-H0: Neexistuje žiadny rozdiel medzi mediánom oboch regiónov.

-H1: Mediány oboch regiónov sú rôzne.

Ak sa mediány zhodujú, potom sa splní nulová hypotéza: Neexistuje žiadny vzťah medzi konzumáciou sódy a regiónom.

A ak sa stane opak, alternatívna hypotéza je pravdivá: existuje vzťah medzi spotrebou a regiónom.

Je to pre tieto prípady, keď je označený test U Mann - Whitney.

Vzorky alebo nepárne vzorky

Nasledujúci dôležitý problém s rozhodnutím, či sa uplatňuje test U Mann Whitney.

Ak sú tieto dve vzorky spárované, použije by sa pôvodná Wilcoxonova verzia. Ale ak nie, ako je to v prípade príkladu, použije sa modifikovaný Wilcoxonov test, ktorý je presne Mann Whitney's Test U.

Mann Whitney U Test Charakteristiky

U -test z Mann -Whitney A neparametrický test, použiteľný na vzorky, ktoré nedodržiavajú normálnu distribúciu alebo s niekoľkými údajmi. Má nasledujúce vlastnosti:

1.- Porovnajte mediány

2.- Pracuje na objednaných rozsahoch

3.- Je to menej silné, pochopením moci Pravdepodobnosť odmietnutia nulovej hypotézy, keď je v skutočnosti nepravdivá.

Berúc do úvahy tieto charakteristiky, použije sa U -test Mann - Whitney, keď:

-Údaje sú nezávislé

-Nesledujú normálne rozdelenie

-Hypotéza NULL H0 je akceptovaná, ak sa médium týchto dvoch vzoriek zhoduje: MA = MB

-Alternatívna hypotéza H1 je akceptovaná, ak sa médium týchto dvoch vzoriek líši: ma ≠ mb

Mann Formula - Whitney

Premenná U je kontrastná štatút použitá v teste Mann - Whitney a je definovaná:

U = min (ua, ub)

To znamená, že u je najmenej z hodnôt medzi UA a UB, aplikované na každú skupinu. V našom príklade by to bolo pre každý región: a o b.

Premenné UA a UB sú definované a vypočítané podľa nasledujúceho vzorca:

Ua = nb + na (Na +1)/2 - ra

Ub = nb + nb (nb +1)/2 - rb

Môže vám slúžiť: zníženie podobných výrazov

Tu hodnoty Na a NB sú veľkosti vzoriek zodpovedajúcich regiónom A a B a na druhej strane, RA a RB sú súčet že budeme definovať nižšie.

Kroky na použitie testu

1.- Objednajte si hodnoty týchto dvoch vzoriek.

2.- Priraďte rozsah objednávky každej hodnote.

3.- Opravte existujúce ligatúry v údajoch (opakované hodnoty).

4.- Vypočítajte RA = súčet rozsahov vzorky a.

5.- Nájdite rb = súčet rozsahov vzorky b.

6.- Stanovte hodnotu UA a UB podľa vzorcov uvedených v predchádzajúcej časti.

7.- Porovnajte UA a UB a maloletý z nich je priradený k alebo experimentálnej štatistike (tj údaje) v porovnaní s teoretickou alebo normálnou štatistikou.

Praktické uplatňovanie aplikácie

Teraz uplatňujeme vyššie uvedené na problém sódy, ktorá bola predtým vyvinutá:

Región A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Región B: 12,14, 11, 30, 10

V závislosti od toho, že prostriedky obidvoch vzoriek sú štatisticky rovnaké alebo odlišné, pokračujeme v akceptovaní alebo odmietnutí nulovej hypotézy: Neexistuje žiadny vzťah medzi premennou a X, to znamená, že konzumácia sódy nezávisí od regiónu:

H0: MA = MB

H1: ma ≠ mb

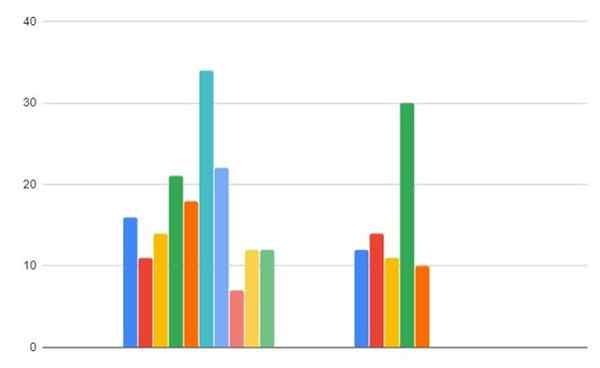Obrázok 2. Údaje o plynnej spotrebe v oblastiach A a B. Zdroj: f. Zapata.

- Krok 1

Pokračujeme v objednávaní údajov spoločne pre tieto dve vzorky a usporiadame hodnoty od najmenej po najväčšie:

Všimnite si, že hodnota 11 sa objaví 2 -krát (raz v každej vzorke). Pôvodne má pozície alebo rozsahy 3 a 4, ale nie nadhodnotenie alebo podceňovanie jedného alebo druhého, priemerná hodnota je vybraná ako rozsah, to je 3,5.

Podobne sa hodnota 12 prebieha, ktorá sa opakuje trikrát s rozsahmi 5, 6 a 7.

Hodnota 12 je priradená priemerný rozsah 6 = (5+6+7)/3. A to isté pre hodnotu 14, ktorá má ligáciu (objavené v obidvoch vzorkách) v pozíciách 8 a 9, je priradený priemerný rozsah 8.5 = (8+9)/2.

- Krok 2

Údaje pre oblasť A a B sa potom opäť oddelia, ale teraz sú ich zodpovedajúce rozsahy priradené v inom riadku:

Región a

Región B

Rozsahy RB sa získavajú zo súm prvkov druhého riadku pre každý prípad alebo oblasť.

Krok 3

Vypočítajú sa príslušné hodnoty UA a UB:

UA = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

Ub = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Experimentálna hodnota u = min (19, 31) = 19

Krok 4

Teoretik má sledovať normálne rozdelenie n s parametrami danými výlučne veľkosťou vzoriek:

Môže vám slúžiť: Iracionálne čísla: História, vlastnosti, klasifikácia, príklady

N ((Na zajtranb) /2, √ [nb (Na + nb +1) /12])

Na porovnanie premennej alebo experimentálne získanej, s teoretickou, je potrebné vykonať zmenu premennej. Prechádza z premennej alebo experimentuje s jej hodnotou typický, Ktorý sa bude volať Z, Aby bolo možné porovnávať s typom normálneho rozdelenia.

Zmena premennej je nasledovná:

Z = (u - na.Nb / 2) / √ [NA. NB (Na + NB + 1) / 12] 

Je potrebné poznamenať, že pri zmene premennej sa použili parametre teoretického rozdelenia pre u. Potom nová premenná Z, ktorá je hybridom medzi teoretickým a experimentálnym alebo normálnym distribúciou typizovaným n (0,1).

Porovnávacie kritériá

Ak z ≤ zα ⇒ Hypotéza NULL H0 je akceptovaná

Áno z> Zα ⇒ Hypotéza NULL H0 je zamietnutá

Kritické hodnoty Zα typované závisia od požadovanej úrovne spoľahlivosti, napríklad pre úroveň dôvery a = 0,95 = 95%, ktorá je najbežnejšia, má kritickú hodnotu Zα = 1,96.

Pre údaje uvedené tu:

Z = (u - nb / 2) / √ [nb (Na + nb + 1) / 12] = -0,73

Ktorá je pod kritickou hodnotou 1,96.

Potom konečný záver je, že je akceptovaná nulová hypotéza:

Neexistuje žiadny rozdiel v spotrebe sódy medzi regiónmi A a B.

Online kalkulačky pre U -test Mann - Whitney

Existujú konkrétne programy pre štatistické výpočty vrátane SPSS a Minitab, ale tieto programy sa platia a ich použitie nie je vždy jednoduché. Je to preto, že poskytujú toľko možností, že jeho použitie je prakticky vyhradené pre odborníkov na štatistiku.

Našťastie existuje niekoľko veľmi presných, bezplatných a jednoduchých -použitých online programov, ktoré okrem iného umožňujú testy U -Whitney U.

Tieto programy sú:

-Štatistika sociálnej vedy (Socscistatistics.com), ktorý má test U-Whitney U a Wilcoxon's v prípade vyvážených alebo párových vzoriek.

-Štatistika terapie AI (AI-Therapia.com), ktorý má niekoľko obvyklých opisných štatistických testov.

-Štatistické použitie (fyzika.Csbsju.Edu/štatistiky), jeden z najstarších, takže vaše rozhranie môže vyzerať zastarane, hoci ide o veľmi efektívny bezplatný program.

Odkazy

1. Dietrichson. Kvantitatívne metódy: Test rozsahov. Obnovené z: rezervovanie.orgán
2. Marín J P. Sprievodca SPSS: Analýza a postupy v neparametrických testoch. Získané z: Halweb.Uc3m.je
3. Unáhleň. Neparametrický test: u Mann - Whitney. Obnovené z: YouTube.com
4. Wikipedia. U -test Mann - Whitney. Obnovené z: je.Wikipedia.com
5. Xlstat. Centrum pomoci. Mann Test Tutorial - Whitney v Exceli. Získané z: pomoci.XLSAT.com