Rovnica kontinuity

Vysvetľujeme, čo je rovnica kontinuity, jej vzorec, aplikácie, príklady a navrhujeme cvičenia na vyriešenie

Aká je rovnica kontinuity?

Ten rovnica kontinuity, V prípade nestlačiteľnej tekutiny sa uvádza, že celková hmotnosť tekutiny, ktorá cirkuluje trubicou bez straty alebo ziskov, zostáva konštantná. Inými slovami, cesto je zachované bez zmien, keď sa tekutina pohybuje.

Nespresiteľná tekutina je taká, že ktorej hustota zostáva pri tečú. Napríklad voda je kvapalina považovaná za nestlačiteľnú za štandardných tlakových a teplotných podmienok.

Existuje matematický spôsob vyjadrenia zachovania hmoty v rovnici kontinuity, ktorú dal:

Do₁∙ v₁ = A₂∙ v₂

Kde v₁ a v₂ Predstavujú rýchlosť tekutiny v dvoch častiach potrubia, zatiaľ₁ už₂ Sú to príslušné krížové oblasti.

Produkt prierezovej oblasti sa nazýva rýchlosť pretekať A rovnica kontinuity naznačuje, že v celom potrubí je tok konštantný. Tok je tiež známy ako objemový prietok, Rozumie sa starostlivým pozorovaním predchádzajúceho výrazu, ktorého rozmery sú objem na jednotku času.

Vzorec

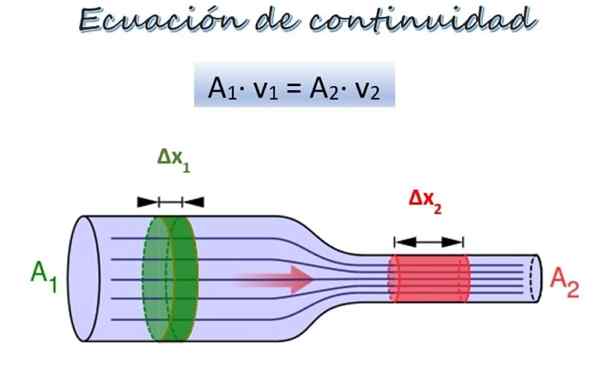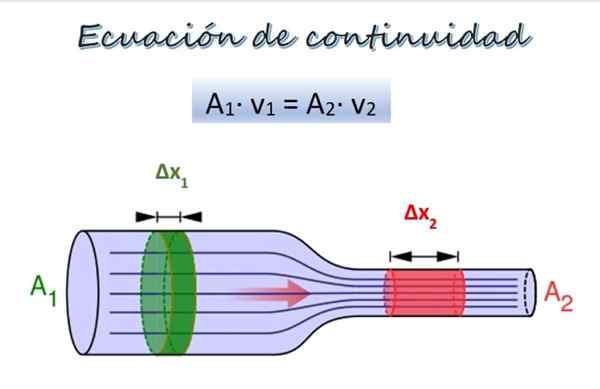
Rovnica kontinuity pre tok tekutiny pozdĺž rúrky s rôznymi priemermi. Zdroj: Wikimedia Commons/F. Zapata.

Na hornom obrázku je potrubie s dvoma časťami rôznych priemerov a v rovnakej výške, hoci by mohli byť v rôznych výškach bez toho, aby predstavovali problém.

V oddiele 1, širšia, prierezová oblasť je₁ a tekutina sa pohybuje rýchlosťou v₁, Zatiaľ čo v oddiele 2, užší, oblasť prierezu je₂ a rýchlosť tekutiny je V₂.

Časť cesta ΔM₁ (zelená) sa pohybuje podľa oddielu 1 v čase Δt. Počas tohto obdobia časť ΔM₂ (červená) Cestujte cez oddiel 2. Pretože tekutina je nestlačiteľná, jej hustota je rovnaká vo všetkých jej bodoch, takže od definície hustoty:

Môže vám slúžiť: Gase Constant: Čo je, výpočet a príklady

Tu je hustota, m je hmotnosť a objem V. Podľa toho hmotnosť ΔM₁ rovná sa:

ΔM₁ = ρ ∙ V₁

Kde objem V₁ Je to produkt medzi prierezom a vzdialenosťou δx₁:

ΔM₁ = ρ ∙ (a₁ ∙ δx₁)

Ale odvtedy:

Potom časť cesta ΔM₁ Môžete písať, pokiaľ ide o rýchlosť a čas Δt ako:

ΔM₁ = ρ ∙ a₁ ∙ δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ ΔT)

Analóg Časť ΔM je napísaná₂ To tečie súčasne podľa oddielu 2:

ΔM₂ = ρ ∙ a₂ ∙ δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ ΔT)

Zachovaním omše:

ΔM₁ = ΔM₂

A:

ρ ∙ a₁ ∙ v₁ ∙ Δt = ρ ∙ a₂ ∙ v₂ ∙ Δt

Pretože Δt a ρ sú zrušené, výsledky:

Do₁ ∙ v₁ = A₂ ∙ v₂

Tok q

Produkt prierezu A rýchlosťou tekutiny V sa nazýva prietok a označuje ako Q. Je ekvivalentný objemu tekutiny na jednotku času cez potrubie alebo objemový prietok:

 V objem a Δt časový interval. Prietok v medzinárodnom systéme jednotiek je m³/s, hoci kubické nohy, galóny/min, galóny/s litre/s a galóny/s sú časté. Niektoré z najpoužívanejších konverzných faktorov sú nasledujúce:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/s
• 1 ft³/S = 0.0283168 m³/s
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850,3 gal/min

Všimnite si, že znížením prierezu skúmavky sa rýchlosť tekutiny zvyšuje a naopak, ak sa prierez zvyšuje, rýchlosť sa zníži tak, aby prietok bol konštantný.

Aplikácie a príklady

Rovnica kontinuity sa používa pri analýze prietoku tekutín v kombinácii s rovnicou Bernoulli, v ktorej sa zohľadňujú variácie rýchlosti tekutiny v rôznych častiach, ako aj zmeny tlaku a účinok výšky.

Môže vám slúžiť: Priamy prúd

Príklad 1

V rodinnej záhradnej hadici, keď voda normálne opúšťa prúd, má určitý rozsah, ale ak položí prst na výstup z hadice, čím sa zníži výstupný otvor, rozsah prúdu je väčší.

Tu je rovnica kontinuity splnená, pretože znížením plochy výstupnej dýzy sa rýchlosť prúdu zvyšuje tak, aby plocha rýchlosti rýchlosťou bola konštantná.

Príklad 2

Vodný prúd sa zužuje, keď padá, pretože jeho rýchlosť sa zvyšuje. Týmto spôsobom zostáva rýchlosť produktu na plochu konštantná

Ďalším príkladom, v ktorom sa zvýrazní rovnica kontinuity.

Týmto spôsobom je tok konštantný, zatiaľ čo prúd naďalej prúdi v laminárnom režime, to znamená, že voda jemne padá bez turbulencie alebo víri.

Vyriešené cvičenia

Cvičenie 1

Voda cirkuluje rúrkou s priemerom 20 cm. S vedomím, že tok je 2000 l/s, nájdite rýchlosť vody v potrubí.

• Riešenie

Je vhodné vyjadriť všetko v jednotkách medzinárodného systému. Po prvé, vypočíta sa krížová sekcia potrubia a nezabudnite, že polomer je polovica priemeru:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Preto je oblasť:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Tok je vyjadrený v m³/s pomocou vhodného konverzného faktora:

Q = 2000 l/s = 2 m³/s

Z vzorca q = a ∙ v Rýchlosť, s akou sa tekutina cirkuluje cez potrubie, je vyčistená:

Cvičenie 2

Máte variabilný prierezový potrubie, cez ktoré prúdi voda. V určitom bode je prierez 0.070 m² A rýchlosť vody je 3.50 m/s. Vypočítať:

Môže vám slúžiť: Pascal Principle: História, aplikácie, príklady

a) Rýchlosť vody v inom bode v potrubí, ktorej plocha prierezu je 0.105 m².

b) Objem vody, ktorý je vypustený otvorenými koniec za 1 hodinu.

• Roztok

Používa sa rovnica kontinuity, ktorá zodpovedá toku prvého bodu s tokom druhého. Tok je:

Q = A ∙ V

Pre kontinuitu:

Otázka₁ = Q₂

Do₁ ∙ v₁ = A₂ ∙ v₂

Teraz nahradia údaje poskytnuté vyhlásením:

• Do₁ = 0.070 m²
• vložka₁ = 3.50 m/s
• Do₂ = 0.105 m²
• vložka₂ =?

A vyčistí v₂:

Riešenie B

Pretože tok je tiež objem na jednotku času, musí:

Preto zväzok V je:

V = q ∙ Δt = (a ∙ v) Δt

Prietok, ktorý sa dá vypočítať s údajmi bodu 1 alebo v bode 2, pretože je rovnaký v oboch bodoch:

Q = a₁ ∙ v₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Vediac, že ​​1 hodina = 3600 s, objem prepustenej vody je:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

Za 1 hodinu 882 m sa stiahne³ vody cez potrubie.