Clausius-Clapeyronova rovnica, pre čo ide, príklady, cvičenia
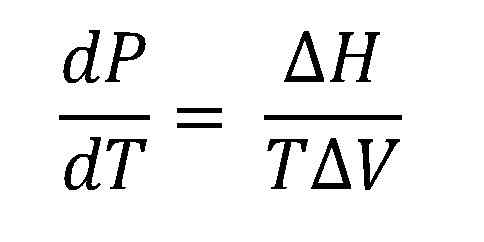
- 2032
- 330
- Alan Milota
Ten Clausius-Clapeyronova rovnica Je to ten, ktorý spája zmeny v tlaku pary a teploty, vo fáze alebo zmene prechodu stavu. Uplatňuje sa na sublimácie, odparovanie, fúzie alebo dokonca v zmenách v kryštalických fázach. Za zmienku stojí, že táto rovnica sa vzťahuje na čistú látku, ktorá je v rovnováhe.
Táto rovnica odvodzuje z termodynamických zákonov a P-diagramov pre látku, kde je pozorovaná koexistencia; To, čo oddeľuje dve rôzne fázy (kvapalina-vapor, tuhá látka atď.). Na prenos tejto čiary je potrebný zisk alebo strata tepla, ako je entalpia odparovania, ΔHVrece.
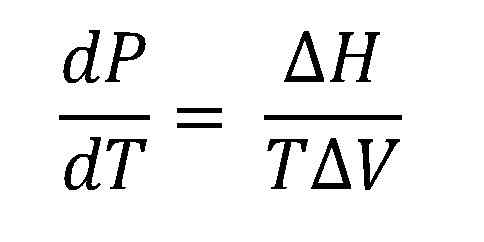 Clausius-Clapeyronova rovnica. Zdroj: Gabriel Bolívar.
Clausius-Clapeyronova rovnica. Zdroj: Gabriel Bolívar. Vyšší obrázok ukazuje Clausius-Clapeyronova rovnicu pred integráciou. Normálne sa zvyčajne aplikuje na systémy kvapalných látok, kde sa používa AHVrece a chcete vypočítať, aký bude tlak kvapalnej pary pri určitej teplote. Slúži tiež na výpočet AHVrece určitej kvapaliny v teplotnom rozsahu.
Clausisu-clapeyronova rovnica sa tiež často používa na štúdium zmeny tlaku v prchavých tuhých látkach; To znamená, že sa berie do úvahy entalpia sublimácie, ΔHponorka.
[TOC]
Čo je Clausisu-clapeyronova rovnica pre?
Výpočet tlakov tlakov a entalpie odparovania
Z rovnice Clausius-Clapeyron Zhora sa konečne urobia niektoré matematické úvahy, aby sa konečne vykonala integrácia. Napríklad pre systém kvapaliny-vapor sa predpokladá, že AHVrece Nemení sa s teplotou a že AV zodpovedá výlučne objemu pary, opovrhuje objem kvapaliny (vpary-Vložkatekutý = Vpary).
Za predpokladu, že para sa správa ako ideálny plyn a integrácia, sa získa rovnica integrovaného Clausius-Clapeyron:
Môže vám slúžiť: volatilizácia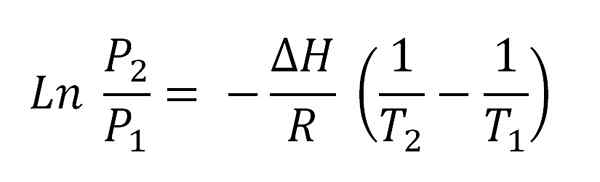 Clausius-Clapeyronova rovnica integrovaná.
Clausius-Clapeyronova rovnica integrovaná. Táto rovnica zodpovedá rovnici riadku, ktorá je grafická ako:
Ln P vs 1/t
A ktorého negatívny sklon je (AH/R). Na splnenie tejto rovnice musí byť preto AH konštantná v teplotnom intervale (t2-Tón1), v ktorých sa meria tlaky pary v rovnováhe s kvapalinou.
Týmto spôsobom, ak sa predpokladá, že AH sa v malých teplotných intervaloch mení, je možné použiť rovnicu tejto čiary na predpovedanie zmien tlaku pár kvapaliny; A ešte viac, môžete určiť jeho ΔH odparovania.
Čím väčšie sa uvažujú intervaly teploty, najväčšia odchýlka tejto rovnice experimentálnych údajov a tým menej sa splní.
Stanovenie fázových zmien
Clausius-Clapeyronova rovnica sa tak stáva vývojom dotyčnicovej línie k spoločnej línii medzi dvoma fyzikálnymi fázami, ktorá sa pozoruje v akomkoľvek P-diagrame látky pre látku.
Ak dôjde k zmene fázy, dôjde k zmene svahu a δH nebude rovnaká. Preto, keď sa preukáže silné odchýlky a zlyhá rovnica, je to znak, že v intervale teploty prežije iná fázová zmena. To znamená, že prestane byť systémom kvapaliny-vapor, pretože sa odovzdáva do koexistenčnej čiary zodpovedajúcej vyrovnávaniu tuhej kvapaliny alebo tuhej látky.
Použite príklady
- Rovnica Clausius-Clapeyron sa používa v meteorológii na štúdium správania oblakov, dokonca aj na tých, ktoré sú prítomné na iných planétach alebo mesiacoch s atmosférou.
Môže vám slúžiť: kyselina glukónová: Štruktúra, vlastnosti, syntéza, použitie- Používa sa pri určovaní fúznej entalpie niekoľkých kovov, ako je sodík a gallium, a na extrapolovanie ich tlakov pary pri veľmi vysokých teplotách.
- Používa sa tiež na stanovenie entalpie odparovania látok, ako je plynný chlór, tetrachlorid uhlíka, kvapalná voda, ľad a jód.
- Slúži tiež na štúdium fázových zmien v kryštalických štruktúrach. V tomto poslednom príklade vyzerá integrovaná rovnica Clausius-Clapeyron pozoruhodne odlišne, pretože rovnaké úvahy, ktoré sa berú pre systém kvapaliny-vapor. Zmeny objemu z jednej fázy do druhej sú malé.
Vyriešené cvičenia
- Cvičenie 1
Tlak ľadovej pary je 4.58 Torr pri 0 ° C a 1.95 Torr A -10 ° C. Aká je vaša sublimačná entalpia v tomto teplotnom rozsahu?
Všimnite si, že máme dva tlaky a dve teploty:
P1 = 4.58 torr
P2 = 1.95 torr
Tón1 = 0 ° C + 273 = 273 K
Tón2 = -10 ° C + 273 = 263 K
Konvertujeme teplotné jednotky z ° C na k, pretože konštanta R plynov má vo svojich jednotkách k:
R = 8.314 J/K
Používame teda integrovanú rovnicu Clausius-Clapeyron a Clear AHponorka, čo by zostalo ako:
ΔHponorka = -Rln (P2/P1) / (1 / t2 - 1 /t1)
Pre viac pohodlia bude nahradiť iba čísla, ale s vedomím, že poslednou jednotkou bude Joule:
ΔHponorka = -(8.314) LN (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Alebo 51.07 j berúc do úvahy niekoľko desatinných miest. Táto hodnota bude predstavovať kmity v závislosti od intervalov T2-Tón1 a určitých parných tlakov.
- Cvičenie 2
Bod etanolu varu pri tlaku 760 torr (1 atm) je 78.3 ° C a jej entalpia odparovania je 39.3 kJ. Aký bude váš tlak pary pri teplote 46 ° C?
Môže vám slúžiť: Tantalus: Štruktúra, vlastnosti, použitia, získanieIdentifikujeme údaje:
P1 = 760 torr
P2 = ?
Tón1 = 78.3 ° C + 273 = 351.3 k
Tón2 = 46 ° C + 273 = 319 K
ΔHVrece = 39.3 kJ alebo 39300 j
Takže musíme vyčistiť P2 integrovanej rovnice Clausius-Clapeyron. Jednotky budú opäť vynechané z dôvodu pohodlia a výpočty sa vyvinú krok za krokom:
LN (P2/P1) = -(ΔHVrece/R) (1/t2 - 1/t1)
LN (P2/760) = -(39300/8.314) (1/319 - 1/351.3)
LN (P2/760) = -1.36
Použitie exponenciálnej funkcie na oboch stranách rovnice, aby bolo možné vyčistiť P2 budeme mať:
E (ln p2/760) = e(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 torr
Pri nižšej teplote (46 ° C), nižší tlak pary (195 torr). V skutočnosti, keď etanol má tlak 760 Torr na 78.3 ° C, hovoríme o jeho normálnom bode varu. Toto je správanie očakávané pre všetky tekutiny
Všeobecne platí, že cvičenia tohto typu Clausius-Clapeyron pozostávajú z zúčtovania P2, Tón2 alebo ΔH odparovania alebo sublimácie. Výpočty sa významne menia, keď by sa malo zvážiť aj AV, najmä pokiaľ ide o systémy alebo zostatky z pevných látok.
Odkazy
- Whitten, Davis, Peck & Stanley. (2008). Chémia. (8. vydanie.). Učenie sa.
- Wikipedia. (2020). Vzťah Clausius-Clapeyron. Zdroj: In.Wikipedia.orgán
- Štátna univerzita v San José. (s.F.). Rovnica Clausius-Clapeyron:
Derivácia a aplikácia STI v meteorológii. Získané z: SJSU.Edu - Skupina Bodner. (s.F.). Clausius-Clapeyronova rovnica. Zdroj: Chemed.Chem.Purdue.Edu
- Chieh c. & Censulo a. (18. mája 2020). Clausius-Clapeyronova rovnica. Chémia librettexts. Získané z: Chem.Librettexts.orgán
- Walter J. Moore. (1962). Fyzikálna chémia. (Štvrté vydanie). Longmans.

