Hypergeometrické distribučné vzorce, rovnice, model

Ten hypergeometrická distribúcia Je to diskrétna štatistická funkcia, ktorá je primeraná na výpočet pravdepodobnosti v náhodných experimentoch s dvoma možnými výsledkami. Podmienka potrebná na jeho použitie je, že ide o malé populácie, v ktorých sa extrakcie nevymenia a pravdepodobnosti nie sú konštantné. 

Preto, keď je zvolený prvok populácie, aby poznal výsledok (pravdivý alebo nepravdivý) určitej charakteristiky, ten istý prvok sa nemôže znova zvoliť.

postava 1. V populácii takýchto skrutiek sú určite chybné vzorky. Zdroj: Pixabay.

Ďalší zvolený prvok určite je pravdepodobnejšie, že získa skutočný výsledok, ak predchádzajúci prvok mal negatívny výsledok. To znamená, že pravdepodobnosť sa mení, pokiaľ sa extrahujú prvky vzorky.

Hlavné aplikácie hypergeometrickej distribúcie sú: kontrola kvality v procesoch s malou populáciou a výpočet pravdepodobností v náhodných hrách.

Pokiaľ ide o matematickú funkciu, ktorá definuje hypergeometrickú distribúciu, pozostáva z troch parametrov, ktoré sú:

- Číslo prvkov populácie (n)

- Veľkosť vzorky (m) 

- Počet udalostí v kompletnej populácii s priaznivým (alebo nepriaznivým) výsledkom študovaného charakteristiky (N).

[TOC]

Vzorce a rovnice

Hypergeometrický distribučný vzorec poskytuje pravdepodobnosť P o čom X Vyskytujú sa priaznivé prípady určitej charakteristiky. Cesta matematického písania v závislosti od kombinatorických čísel je:

V predchádzajúcom výraze N, n a m Sú to parametre a X samotná premenná. 

-Celková populácia je N.

-Počet pozitívnych výsledkov určitej binárnej charakteristiky vzhľadom na celkovú populáciu je n.

-Počet prvkov vzorky je m.

V tomto prípade, X Je to náhodná premenná, ktorá má hodnotu X a P (x) označuje pravdepodobnosť výskytu X priaznivé prípady študovanej charakteristiky.

Dôležité štatistické premenné

Ďalšie štatistické premenné pre hypergeometrickú distribúciu sú:

- Polovica μ = m*n/n

- Rozptyl σ^2 = m*(n/n)*(1-N/n)*(n-m)/(n-1)

- Typická odchýlka σ čo je druhá odmocnina rozptylu.

Model a vlastnosti 

Aby sa dostal k hypergeometrickému distribučnému modelu, je založený na pravdepodobnosti získania X priaznivé prípady vo vzorke veľkosti m. Táto vzorka obsahuje prvky, ktoré spĺňajú študovanú nehnuteľnosť, a prvky, ktoré nie sú.

Pamätaj si to n predstavuje počet priaznivých prípadov v celkovej populácii N predmety. Potom by sa pravdepodobnosť vypočítala takto:

Môže vám slúžiť: Vektorový priestor: základňa a rozmer, axiómy, vlastnosti

P (x) = (# spôsobov, ako získať x# neúspešnými spôsobmi)/(# Celkovým spôsobom výberu)

Vyjadrenie vyššie uvedeného vo forme kombinatorických čísel sa dosiahne nasledujúci model distribúcie pravdepodobností:

Hlavné vlastnosti hypergeometrickej distribúcie

Sú nasledujúce:

- Vzorka musí byť vždy malá, hoci populácia je veľká.

- Prvky vzorky sa extrahujú z jednej, bez toho, aby ich znova začlenili do populácie.

- Nehnuteľnosť, ktorá sa má študovať, je binárna, to znamená, že môže mať iba dve hodnoty: 1 ani 0, O dobre Pravdivý ani vylúčiť.

V každom kroku extrakcie sa pravdepodobnosť mení v závislosti od predchádzajúcich výsledkov.

Prístup binomickým rozdelením

Ďalšou vlastnosťou hypergeometrickej distribúcie je to, že sa k nej dá osloviť binomickým rozdelením, označovaná ako Bitka, Pokiaľ populácia N byť veľký a najmenej 10 -krát väčší ako vzorka m. V tomto prípade by to bolo také:

P (n, n, m; x) = bi (m, n/n, x)           

Pokiaľ je n veľký a n> 10 m

Príklady

Príklad 1

Predpokladajme, že stroj, ktorý vytvára skrutky a akumulované údaje, naznačuje, že 1% vyjde s defektmi. Potom v krabici n = 500 skrutiek bude počet defektov:

N = 500 * 1/100 = 5

Pravdepodobnosti prostredníctvom hypergeometrického rozdelenia

Predpokladajme, že z tejto škatule (tj tejto populácie) berieme vzorku M = 60 skrutiek.

Pravdepodobnosť, že žiadna skrutka (x = 0) z listov vzorky je defektná, je 52,63%. Tento výsledok sa dosiahne pri použití funkcie hypergeometrickej distribúcie:

P (500, 5, 60; 0) = 0,5263

Pravdepodobnosť, že X = 3 vzorové skrutky zanechávajú chybné, je: P (500, 5, 60; 3) = 0,0129.

Na druhej strane pravdepodobnosť, že x = 4 skrutky šesťdesiatych rokov nechávajú chybné, je: P (500, 5, 60; 4) = 0,0008.

Nakoniec pravdepodobnosť, že x = 5 skrutiek v tejto vzorke vyjde s defektom, je: P (500, 5, 60; 5) = 0.

Ale ak chcete poznať pravdepodobnosť, že v tejto vzorke sú viac ako 3 chybné skrutky, musí sa získať akumulovaná pravdepodobnosť a dodať:

P (3)+P (4)+P (5) = 0,0129+0,0008+0 = 0,0137.

Tento príklad je znázornený na obrázku 2, získaný pomocou použitia Geogebra Široký používať bezplatný softvér na školách, inštitúciách a univerzitách.

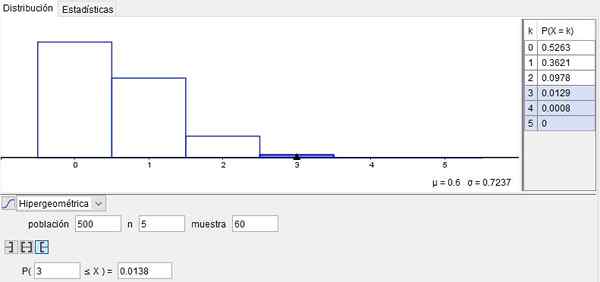Obrázok 2. Príklad hypergeometrickej distribúcie. Pripravený spoločnosťou F. Zapata s geogebou.

Príklad 2

Španielska paluba má 40 kariet, z ktorých 10 má zlato a zvyšných 30 ho nemá. Predpokladajme, že z tejto paluby sa extrahuje 7 kariet, ktoré sa nevracia na palubu.

Môže vám slúžiť: Centrálna symetria: Vlastnosti, príklady a cvičenia

Ak x je počet zlatých prítomných v 7 extrahovaných kartách, potom pravdepodobnosť, že X oros v extrakcii 7 kariet je daná hypergeometrickým distribúciou P (40,10,7; x).

Pozrime sa na to: Na výpočet pravdepodobnosti 4 zlata v extrakcii 7 kariet používame vzorec hypergeometrickej distribúcie s nasledujúcimi hodnotami:

A výsledkom je: 4,57% pravdepodobnosť.

Ale ak chcete poznať pravdepodobnosť získania viac ako 4 kariet, budeme musieť pridať:

P (4)+p (5)+p (6)+p (7) = 5,20%

Vyriešené cvičenia

Nasledujúci súbor cvičení je určený na ilustráciu a asimiláciu konceptov, ktoré boli uvedené v tomto článku. Je dôležité, aby sa čitateľ pokúšal vyriešiť ich sami, skôr ako sa pozrie na riešenie.

Cvičenie 1

Profylaktická továreň zistila, že z každých 1 000 kondómov vyrobených určitým strojom je 5 chybných. Na vykonanie kontroly kvality je náhodne odobraté 100 kondómov a časť je zamietnutá, ak je aspoň jeden alebo viac chybných. Odpoveď:

a) Aká možnosť musí byť vyradená zo 100 šarží?

b) Je toto kritérium kontroly kvality efektívne?

Riešenie

V tomto prípade sa objavia veľmi veľké kombinatorické čísla. Výpočet je ťažký, pokiaľ nie je k dispozícii primeraný počítačový balík.

Ale pretože ide o veľkú populáciu a vzorka je desaťkrát menšia ako celková populácia, môžete použiť prístup k hypergeometrickej distribúcii v dôsledku binomického rozdelenia:

P (1000,5 100; x) = bi (100, 5/1000, x) = bi (100, 0.005, x) = c (100, x)*0.005^x (1-0.005)^(100-x)

V predchádzajúcom výraze C (100, x) Je to kombinatorické číslo. Potom sa pravdepodobnosť Haya viac ako jedna defektná bude vypočítaná takto:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

Je to vynikajúci prístup, ak v porovnaní s hodnotou získanou pri uplatňovaní hypergeometrického rozdelenia: 0.4102

Dá sa povedať, že 40% pravdepodobnosť, že veľa zo 100 profylaktík by sa malo zlikvidovať, čo nie je príliš efektívne.

Ale byť trochu menej náročný v procese kontroly kvality a zlikvidujte.

Cvičenie 2

Plastový taco stroj funguje takým spôsobom, že z každých 10 kusov je zdeformovaný. Vo vzorke 5 -kusu, že možnosť musí byť chybná jedna kus.

Riešenie

Populácia: n = 10

Môže vám slúžiť: Pythagorovské identity: demonštrácia, príklad, cvičenia

Číslo n defektné pre každé n: n = 1

Veľkosť vzorky: M = 5

P (10, 1, 5; 1) = C (1,1)*C (9,4)/c (10,5) = 1*126/252 = 0.5

Preto existuje 50% pravdepodobnosť, že vo vzorke 5 vychádza taco zdeformované.

Cvičenie 3

Na stretnutí mladých stredných škôl je 7 žien a 6 pánov. Medzi dievčatami, 4 študijné humanitné vedy a 3 vedy. V skupine chlapcov, 1 študuje humanitné a 5 vedy. Vypočítajte nasledujúce:

a) náhodne výber troch dievčat: Aká je pravdepodobnosť, že všetky humanitné vedy študujú?.

b) Ak sú náhodne vybraní traja účastníci na stretnutie priateľov: čo sú traja z nich, bez ohľadu na sex, študujte troch alebo humanitných vied?.

c) Teraz vyberte dvoch náhodných priateľov a zavolajte X k náhodnej premennej „počet tých, ktorí študujú humanitné vedy“. Spomedzi ich zvolených určte priemernú alebo očakávanú hodnotu X a rozptyl σ^2.

Roztok 

Populácia je celkový počet dievčat: n = 7. Tí, ktorí študujú humanitné vedy, sú n = 4, z celkového počtu. Náhodná vzorka dievčat bude m = 3.

V takom prípade je pravdepodobnosť, že títo tromi sú humanitné vedy, daná hypergeometrickou funkciou:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Potom je 11.4% pravdepodobnosť, že tri náhodné humanitné vedy Chicas študujú.

Riešenie B

Hodnoty, ktoré sa majú použiť, sú:

-Populácia: n = 14

-Množstvo, ktoré študuje písmená, je: n = 6 a

-Veľkosť vzorky: M = 3.

-Počet priateľov študujúcich humanitné vedy: x

Podľa toho, x = 3 znamená, že tri humanitné vedy štúdie, ale x = 0 znamená, že žiaden študuje humanitné vedy. Pravdepodobnosť, že tieto tri štúdie to isté, je daná súčtom:

P (14, 6, 3, x = 0) + p (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Potom máme 21% pravdepodobnosť, že traja účastníci stretnutia, ktorí sa náhodne vybrali, študujú to isté.

Riešenie c

Tu máme nasledujúce hodnoty:

N = 14 Celková populácia priateľov, n = 6 Celkový počet v populácii, ktorá študuje humanitné vedy, veľkosť vzorky je m = 2.

Nádej je:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

A rozptyl:

σ (x)^2 =  m*(n/n)*(1-n/n)*(n-m)/(n-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Odkazy

1. Diskrétne rozdelenie pravdepodobnosti. Získané z: Biploot.unavený.je
2. Štatistika. Hypergeometrická distribúcia. Zdroj: ProjectodesCartes.orgán
3. CDPYE-UGR. Hypergeometrická distribúcia. Získané z: ugr.je
4. Geogebra. Classic Geogebra, výpočet pravdepodobnosti. Zotavené z geogebra.orgán
5. Ľahké dedičstvo. Vyriešené hypergeometrické distribučné cvičenia. Získané z: Probafacil.com
6. Minitab. Hypergeometrická distribúcia. Zdroj: Podpora.Minitab.com
7. University of Vigo. Hlavné diskrétne rozdelenie. Získané z: Anapg.webové stránky.Uvigo.je
8. Obviňovač. Štatistika. Získané z: VitUtor.slepo
9. Weisstein, Eric W. Hypergeometrická distribúcia. Obnovené z: Mathworld.Valfram.com
10. Wikipedia. Hypergeometrická distribúcia. Obnovené z: je.Wikipedia.com