Distribučné charakteristiky a cvičenia vyriešené
- 1488
- 62
- Mgr. Pravoslav Mokroš
Ten distribúcia f o Distribúcia Fisher-Sedecor je to, čo sa používa na porovnanie odchýlok dvoch rôznych alebo nezávislých populácií, z ktorých každá sleduje normálne rozdelenie.
Distribúcia, ktorá sleduje rozptyl súboru vzoriek jednej normálnej populácie, je distribúcia Ji-Square (Hrebeň2) stupňa n-1, ak každá zo vzoriek súpravy má n prvky.
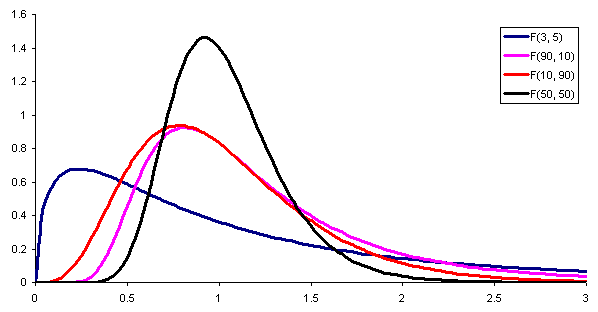
postava 1. Tu je hustota pravdepodobnosti distribúcie F s rôznymi kombináciami parametrov (alebo stupňov voľnosti) čitateľa a menovateľa. Zdroj: Wikimedia Commons. Na porovnanie odchýlok dvoch rôznych populácií je potrebné definovať a štatistický, To znamená pomocnú náhodnú premennú, ktorá umožňuje rozoznať, či majú obe populácie alebo nie sú rovnaké rozptyly.
Táto pomocná premenná môže byť priamo kvocientom odchýlok vzorky každej populácie, v takom prípade, ak je uvedený kvocient blízko jednotky.
[TOC]
Štatistika f a jeho teoretické rozdelenie
Náhodná premenná F alebo štatistická F navrhovaná Ronaldom Fisherom (1890 - 1962) je častejšie používaná na porovnanie odchýlok dvoch populácií a je definovaná nasledovne:
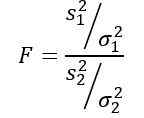
Byť s2 Rozptyl vzorky a σ2 Rozptyl populácie. Na rozlíšenie každej z týchto dvoch skupín obyvateľstva sa používajú predplatné 1 a 2.
Je známe, že distribúcia Ji-Square s (N-1) stupňom slobody je tá, ktorá sleduje pomocnú (alebo štatistickú) premennú, ktorá je definovaná nižšie:
X2 = (N-1) s2 / σ2.
Štatistika F sa preto riadi teoretickým rozdelením uvedeným nasledujúcim vzorcom:
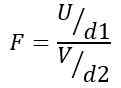
Bytosť Alebo Distribúcia ji-kvadrát s D1 = N1 - 1 stupne slobody pre obyvateľstvo 1 a Vložka Distribúcia ji-kvadrát s D2 = n2 - 1 stupne slobody pre obyvateľstvo 2.
Môže vám slúžiť: Vektorová algebraPomer definovaný týmto spôsobom je nové rozdelenie pravdepodobnosti, známe ako distribúcia f s D1 stupne voľnosti v čitateľovi a D2 stupne slobody v menovateľovi.
Priemer, móda a rozptyl distribúcie f
Polovica
Priemerná distribúcia F sa vypočíta takto:
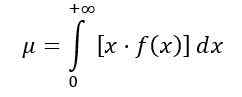
Byť f (x) hustota pravdepodobnosti distribúcie F, ktorá je znázornená na obrázku 1 pre niekoľko kombinácií parametrov alebo stupňov voľnosti.
Môžete napísať hustotu pravdepodobnosti f (x) v závislosti od funkcie y (funkcia gama):
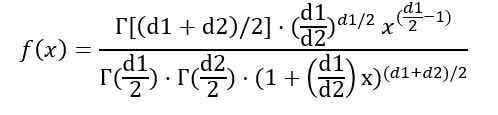
Akonáhle je integrál uvedený predtým, dospelo sa k záveru, že priemer distribúcie F s stupňami slobody (D1, D2) je: IS: IS: IS: IS: IS: IS: IS: IS: IS:
μ = d2 / (d2 - 2) s d2> 2
Kde to ukazuje, že napodiv, priemer nezávisí od stupňov slobody D1 čitateľa.
Formovať
Na druhej strane móda závisí od D1 a D2 a je daná:
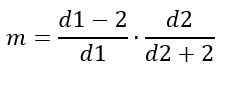
Pre d1> 2.
Rozptyl distribúcie f
Rozptyl σ2 distribúcie F sa vypočíta z integrálu:
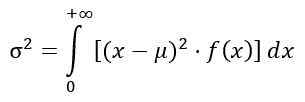
Získanie:
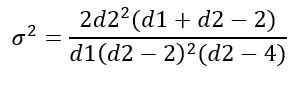
Riadenie distribúcie f
Rovnako ako iné kontinuálne distribúcie pravdepodobnosti, ktoré zahŕňajú zložité funkcie, aj distribučná správa sa vykonáva podľa tabuliek alebo softvérom.
Distribučné tabuľky f
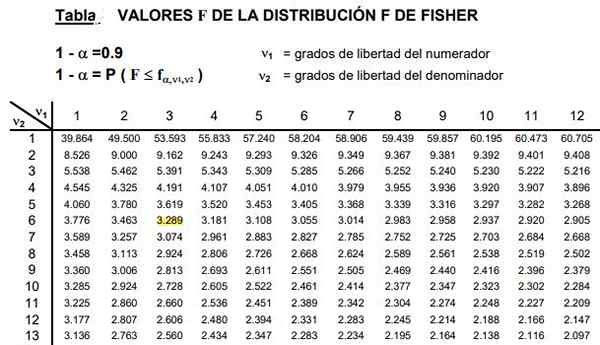Obrázok 2. Je uvedená časť tabuľky distribúcie F, ktorá je zvyčajne veľmi rozsiahla, pretože existuje široká kombinácia možných stupňov voľnosti D1 a D2. Tabuľky zahŕňajú dva parametre alebo stupne voľnosti distribúcie F, stĺpec označuje stupeň voľnosti čitateľa a rad. Stupeň voľnosti menovateľa.
Môže vám slúžiť: Nerovnosť trojuholníka: demonštrácia, príklady, vyriešené cvičeniaObrázok 2 zobrazuje časť tabuľky distribúcie F pre prípad a významnosť 10%, to je a = 0,1. Hodnota F je zvýraznená, keď D1 = 3 a D2 = 6 s úroveň sebavedomia 1- a = 0,9, to je 90%.
Softvér pre distribúciu f
Pokiaľ ide o softvér, ktorý spravuje distribúciu F, existuje veľká rozmanitosť, od tabuľiek ako Vynikať dokonca aj špecializované balíčky, ako napríklad Minitab, SPSS a R Vymenovať niektoré z najznámejších.
Je potrebné poznamenať, že softvér na geometriu a matematiku Geogebra Má štatistický nástroj, ktorý obsahuje hlavné distribúcie vrátane distribúcie F. Obrázok 3 zobrazuje distribúciu F pre prípad D1 = 3 a D2 = 6 úroveň sebavedomia 90%.
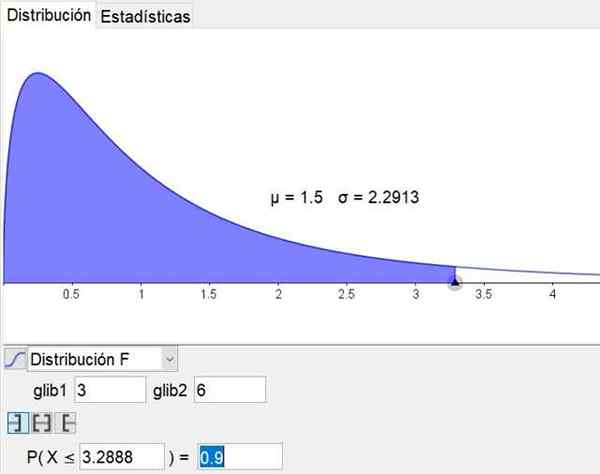Obrázok 3. Distribúcia F je uvedená pre prípad D1 = 3 a D2 = 6 s 90%úrovňou spoľahlivosti, získaného prostredníctvom štatistického nástroja Geogebra. Zdroj: Geogebra.orgán Vyriešené cvičenia
Cvičenie 1
Zvážte dve vzorky populácií, ktoré majú rovnaký rozptyl populácie. Ak je vzorka 1 veľkosť n1 = 5 a vzorka 2 je veľkosť n2 = 10, určte teoretickú pravdepodobnosť, že pomer jej príslušných odchýlok je menší alebo rovný 2.
Riešenie
Malo by sa pamätať na to, že štatistika F je definovaná ako:
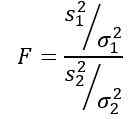
Hovorí sa však, že odchýlky populácie sú rovnaké, takže pre toto cvičenie sa uplatňuje:
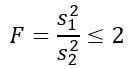
Keďže chcete poznať teoretickú pravdepodobnosť, že tento pomer odchýlok vzorky je menší alebo rovný 2, musíme poznať oblasť v rámci distribúcie F medzi 0 a 2, ktorú je možné získať tabuľkami alebo softvérom. Z tohto dôvodu je potrebné vziať do úvahy, že požadované rozdelenie F má D1 = n1 - 1 = 5 - 1 = 4 a D2 = n2 - 1 = 10 - 1 = 9, to znamená distribúciu f s stupňami voľnosti (4, 9).
Môže vám slúžiť: Séria energie: príklady a cvičeniaPomocou štatistického nástroja Geogebra Bolo zistené, že táto oblasť je 0.82, takže sa dospelo k záveru, že pravdepodobnosť, že pomer odchýlok vzorky je menší alebo rovný 2, je 82%.
Cvičenie 2
Existujú dva procesy výroby tenkých listov. Variabilita hrúbky musí byť čo najviac. Odoberia sa 21 vzoriek každého procesu. Vzorka procesu má štandardnú odchýlku 1,96 mikrónov, zatiaľ čo proces procesu B má štandardnú odchýlku 2,13 mikrónov. Ktorý z procesov má nižšiu variabilitu? Použite úroveň odmietnutia 5%.
Riešenie
Dáta sú nasledujúce: sb = 2,13 s nb = 21; SA = 1,96 s Na = 21. To znamená, že musíte pracovať s distribúciou F (20, 20) stupňov slobody.
Nulová hypotéza naznačuje, že rozptyl populácie oboch procesov je identická, to znamená σa^2 / σb^2 = 1. Alternatívna hypotéza by znamenala rôzne odchýlky populácie.
Potom, za predpokladu rovnakých odchýlok populácie, je definovaná štatistika F vypočítaná ako: fc = (sb/sa)^2.
Pretože sa hladina odmietnutia považovala za a = 0,05, potom a/2 = 0,025
Distribúcia f (0.025; 20,20) = 0,406, zatiaľ čo f (0.975; 20,20) = 2,46.
Preto nulová hypotéza bude pravdivá, ak vypočítaná f spĺňa: 0,406 Ako FC = (2,13/1,96)^2 = 1,18 sa dospelo k záveru, že štatistika FC je v rozsahu akceptácie nulovej hypotézy s istotou 95%. Inými slovami s istotou 95% oba výrobné procesy majú rovnaký rozptyl populácie.Odkazy