Variabilita

postava 1.- Najznámejšie opatrenia variability. Zdroj: f. Zapata.

Čo sú opatrenia variability?

Ten Variabilita, Tiež sa nazývajú disperzné opatrenia, sú to štatistické ukazovatele, ktoré naznačujú, ako blízko alebo vzdialené údaje ich aritmetického priemeru sa nachádzajú. Ak sú údaje blízko priemeru, distribúcia je koncentrovaná a ak sú ďaleko, je to potom rozptýlené rozdelenie.

Existuje veľa opatrení variability, medzi najznámejšími sú:

• Rozsah
• Priemerná odchýlka
• Rozptyl
• Štandardná odchýlka

Tieto opatrenia dopĺňajú ústredné opatrenia tendencie a sú potrebné porozumieť distribúcii získaných údajov a extrahovať čo najviac informácií.

Rozsah

Rozsah alebo trasa meria amplitúdu súboru údajov. Na určenie jeho hodnoty sa nachádza rozdiel medzi najvyššou hodnotou X_maximálny a najmenej hodnota x_blesk:

R = x_maximálny - X_blesk

Ak údaje nie sú voľné, ale zoskupené podľa intervalu, rozsah sa vypočíta podľa rozdielu medzi hornou hranicou posledného intervalu a dolnou hranicou prvého intervalu.

Ak je rozsah malá hodnota, znamená to, že všetky údaje sú navzájom veľmi blízko, ale veľký rozsah naznačuje, že existuje veľká variabilita. Je zrejmé, že okrem hornej hranice a dolnej hranice údajov tento rozsah nezohľadňuje hodnoty medzi nimi, takže nie je vhodné ich používať, keď je číslo údajov veľké.

Je však okamžitým opatrením na výpočet a má rovnaké dátové jednotky, takže je ľahké ich interpretovať.

Príklad hodnosti

Ďalej je zoznam k dispozícii s počtom cieľov označených cez víkend, vo futbalových ligách z deviatich krajín:

Môže vám slúžiť: aké sú delení z 30? (Vysvetlenie)

40, 32, 35, 36, 37, 31, 37, 29, 39

Je to množina údajov bez zoskupenia. Aby našli tento rozsah, pokračujú v objednávke od najmenej k najväčšiemu:

29, 31, 32, 35, 36, 37, 37, 39, 40

Údaje s najvyššou hodnotou sú 40 cieľov a dáta s najnižšou hodnotou je 29 cieľov, preto rozsah je:

R = 40 - 29 = 11 gólov.

Je možné uvažovať o tom, že rozsah je malý v porovnaní s údajmi o minimálnej hodnote, čo je 29 cieľov, takže sa dá predpokladať, že údaje nemajú veľkú variabilitu.

Priemerná odchýlka

Táto miera variability sa vypočíta prostredníctvom priemeru absolútnych hodnôt odchýlok vzhľadom na priemer. Označovanie priemernej odchýlky ako D_M, Pre údaje, ktoré nie sú v skupine, sa priemerná odchýlka vypočíta podľa nasledujúceho vzorca:

Kde n je počet dostupných údajov, x_Jo Predstavuje každé údaje a x̄ je priemer, ktorý je určený pridaním všetkých údajov a rozdelením medzi n:

Priemerná odchýlka umožňuje v priemere vedieť, koľko jednotiek sa údaje odchyľujú od aritmetického priemeru a majú tú výhodu, že majú rovnaké jednotky ako údaje, s ktorými funguje.

Príklad strednej odchýlky

Podľa údajov z rozsahu je počet označených cieľov:

40, 32, 35, 36, 37, 31, 37, 29, 39

Ak chcete nájsť odchýlku média D_M Z týchto údajov je potrebné najprv vypočítať aritmetický priemer X̄:

A teraz, keď je známa hodnota X̄, pokračujeme v hľadaní priemernej odchýlky_M:

= 2.99 ≈ 3 góly

Preto je možné povedať, že v priemere sa údaje v priemere pohybujú približne v 3 priemerných cieľoch, ktoré sú 35 cieľmi, a ako je uvedené, je to oveľa presnejšia miera ako rozsah.

Môže vám slúžiť: Hyperbola

Rozptyl

Priemerná odchýlka je oveľa tenšia miera variability ako rozsah, ale ako je vypočítaná z absolútnej hodnoty rozdielov medzi každým údajom a priemerom, neponúka väčšiu univerzálnosť z algebraického hľadiska.

Preto je preferovaný rozptyl, ktorý zodpovedá priemeru kvadratického rozdielu každého údajov s priemerom a vypočíta sa pomocou vzorca:

V tomto výraze s² označuje rozptyl a ako vždy x_Jo predstavuje každú z údajov, x̄ je priemer a n celkové údaje.

Pri práci so vzorkou namiesto populácie sa uprednostňuje výpočet rozdielu, ako je táto:

Rozdiel s predchádzajúcim vzorcom je v tom, že v menovateľovi je N - 1 namiesto n. Stáva sa, že rozdelením n, rozptyl vzorky podceňuje rozptyl populácie, z ktorej bola extrahovaná, ale nie keď je rozdelená n - 1. V niektorých textoch, ktoré sa výraz objavia s menom kvázi.

V každom prípade sa rozptyl vyznačuje vždy pozitívnym množstvom, ale je priemerom kvadratických rozdielov, je dôležité poznamenať, že nemá rovnaké jednotky ako jednotky údajov.

Príklad rozptylu

Na výpočet rozptylu údajov o príkladoch rozsahu a priemernej odchýlky sa nahradia zodpovedajúce hodnoty a uvedená súčet. V tomto prípade sa rozhodne rozdeliť medzi N-1:

= 13.86

Štandardná odchýlka

Rozptyl nemá rovnakú jednotku ako v prípade študovanej premennej, napríklad, ak údaje prichádzajú v meračoch, rozptyl vedie k štvorcovým metrom. Alebo v príklade cieľov, ktoré by to bolo v cieľoch na druhú, čo nedáva zmysel.

Môže vám slúžiť: Aké sú prvky podobenstva? (Časti)

Preto je definovaná štandardná odchýlka, nazývaná sa tiež nazývaná typická odchýlka, Rovnako ako druhý koreň rozptylu:

S = √s²

Týmto spôsobom sa miera variability údajov získava v rovnakých jednotkách ako tieto a čím nižšia hodnota S, tým viac zoskupené údaje sú okolo priemeru.

Rozptyl aj štandardná odchýlka sú merania variability, ktoré sa majú zvoliť, keď aritmetický priemer je miera centrálnej tendencie, ktorá najlepšie popisuje správanie údajov.

A je to tak, že štandardná odchýlka má dôležitú vlastnosť, známa ako Chbyshevova veta: najmenej 75% pozorovaní je v intervale definovanom pomocou X ± 2s. Inými slovami, 75% údajov je nanajvýš vo vzdialenosti rovnajúce sa 2 s priemerom.

Podobne, najmenej 89% hodnôt je vo vzdialenosti 3 s priemerom, percento, ktoré je možné rozšíriť, za predpokladu, že je k dispozícii veľa údajov a tieto sa riadia normálnym distribúciou.

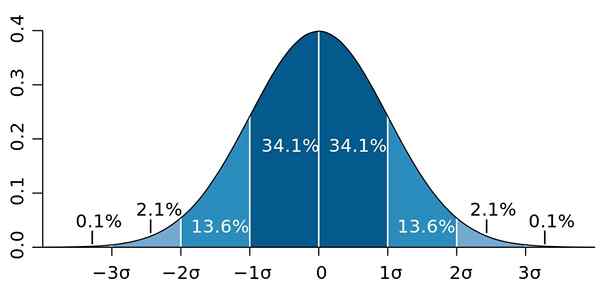
Obrázok 2.- Ak údaje nasledujú normálne rozdelenie, 95.4 z nich sú dve štandardné odchýlky na oboch stranách priemeru. Zdroj: Wikimedia Commons.

Príklad štandardnej odchýlky

Štandardná odchýlka údajov uvedených v predchádzajúcich príkladoch je:

S = √s² = √13.86 = 3.7 ≈ 4 góly