Poissonové distribučné vzorce, rovnice, model, vlastnosti

Ten Poisson Distribúcia Je to diskrétne rozdelenie pravdepodobností, prostredníctvom ktorého môžete poznať pravdepodobnosť, že v rámci veľkej vzorky a počas určitého intervalu sa vyskytuje udalosť, ktorej pravdepodobnosť je malá.

Poissonova distribúcia sa často môže použiť namiesto binomického rozloženia, pokiaľ sú splnené tieto opísané podmienky: veľká vzorka a malá pravdepodobnosť.

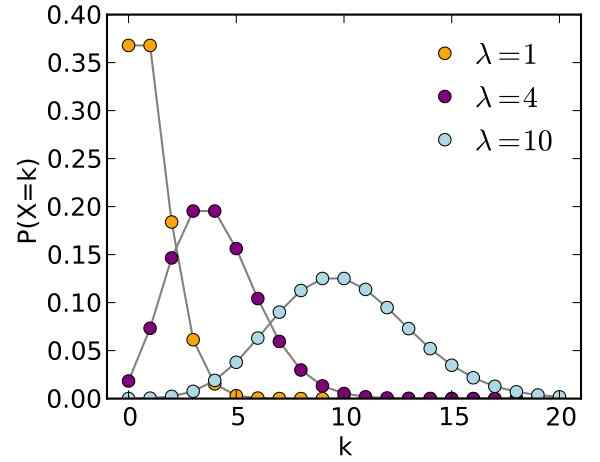
postava 1. Distribučný graf Poisson pre rôzne parametre. Zdroj: Wikimedia Commons.

Siméon-Denis Poisson (1781-1840) vytvoril túto distribúciu, ktorá nesie jeho meno, veľmi užitočné, pokiaľ ide o nepredvídateľné udalosti. Poisson publikoval svoje výsledky v roku 1837, výskumná práca o pravdepodobnosti výskytu chybných trestných trestov.

Následne iní vedci prispôsobili distribúciu v iných oblastiach, napríklad počet hviezd, ktoré by mohli byť v určitom objeme priestoru alebo pravdepodobnosť, že vojak zomrie kvôli Cozovi koňa.

[TOC]

Vzorec a rovnice

Matematická forma Poissonovej distribúcie je nasledovná:

 - Náhodná premenná je a

- μ (niekedy tiež označené ako λ) Je to priemerný alebo distribučný parameter

- Euler číslo: E = 2.71828

- Pravdepodobnosť získania y = k je p

- klimatizovať Je to počet úspechov 0, 1,2,3 ..

- n Je to počet testov alebo udalostí (veľkosť vzorky)

Diskrétne náhodné premenné, ako už názov napovedá, závisia od náhody a berú iba diskrétne hodnoty: 0, 1, 2, 3, 4 ..., k.

Priemer distribúcie je daný:

Rozptyl σ, ktorý meria disperziu údajov, je ďalším dôležitým parametrom. Pre Poissonovu distribúciu je to:

σ = μ

Poisson zistil, že keď n → ∞ a p → 0, priemer μ -tiež sa nazýva μ -tiež nazývaný očakávaná hodnota- Má tendenciu konštantu:

μ → Konštanta

Dôležitý: p Je to pravdepodobnosť výskytu udalosti, ktorá berie do úvahy celkovú populáciu, zatiaľ čo P (y) Je to Poissonova predpoveď o vzorke.

Model a vlastnosti

Poissonova distribúcia má nasledujúce vlastnosti:

-Veľkosť vzorky je veľká: N → ∞.

-Zvažované udalosti alebo udalosti sú navzájom nezávislé a vyskytujú sa náhodne.

-Pravdepodobnosť P Aká určitá udalosť a Vyskytuje sa na konkrétne časové obdobie je veľmi malé: P → 0.

-Pravdepodobnosť viac ako jednej udalosti v časovom intervale je 0.

-Priemerná hodnota je blízko konštantnej danej: μ = n.P (n je veľkosť vzorky)

-Pretože disperzia σ sa rovná μ, pretože prijíma väčšie hodnoty, variabilita je tiež vyššia.

-Udalosti sa musia distribuovať rovnomerne v použitom časovom intervale.

-Sada možných hodnôt udalostí a Je to: 0,1,2,3,4 .. .

Môže vám slúžiť: náhodný experiment: koncept, vzorový priestor, príklady

-Súčet Jo Premenné, ktoré nasledujú po Poissonovej distribúcii, sú tiež ďalšou Poissonovou premennou. Jeho priemerná hodnota je súčtom priemerných hodnôt týchto premenných.

Rozdiely s binomickým rozdelením

Poissonova distribúcia sa líši od binomického rozdelenia v týchto dôležitých aspektoch:

-Binomické rozdelenie je ovplyvnené veľkosťou vzorky S, ako aj pravdepodobnosťou P, Poissonova distribúcia je však ovplyvnená iba priemerom μ.

-V binomickom rozdelení sú možné hodnoty náhodnej premennej a Sú 0,1,2, ..., namiesto toho v distribúcii Poissona neexistuje horná hranica pre tieto hodnoty.

Príklady

Poisson spočiatku uplatnil svoju slávnu distribúciu do právnych prípadov, ale na priemyselnej úrovni bolo jedno z prvých použití vo výrobe piva. V tomto procese sa kvasinkové plodiny používajú na fermentáciu.

Kvasinky pozostávajú zo živých buniek, ktorých populácia je v čase variabilná. Pri výrobe piva je potrebné pridať potrebné množstvo, takže je potrebné poznať množstvo buniek na jednotku objemu.

Počas druhej svetovej vojny sa Poissonova distribúcia používala na to, aby vedeli, či Nemci skutočne ukazovali na Londýn z Calais alebo jednoducho náhodne vystrelili. To bolo pre spojencov dôležité určiť, aká dobrá bola technológia k dispozícii nacistom.

Praktické aplikácie

Poissonove distribučné aplikácie sa vždy vzťahujú na počty časov alebo počítanie priestoru. A keďže pravdepodobnosť výskytu je malá, je známa aj ako „zákon vzácnych udalostí“.

Tu je zoznam udalostí, ktoré spadajú do jednej z týchto kategórií:

-Registrácia častíc v rádioaktívnom rozkladu, ktorý je podobný rastu kvasinkových buniek, je exponenciálna funkcia.

-Počet návštev na určitej webovej stránke.

-Príchod ľudí do radu, aby zaplatili alebo sa zúčastnili (teória chvosta).

-Počet automobilov, ktoré prechádzajú určitým bodom na ceste, pre daný časový interval.

Obrázok 2. Množstvo automobilov, ktoré prechádzajú bodom, nasleduje približne po Poissonovej distribúcii. Zdroj: Pixabay.

-Mutácie utrpeli v určitom reťazci DNA po prijatí vystavenia žiareniu.

-Počet meteorov priemeru viac ako 1 m klesol za rok.

-Defekty na štvorcový meter tkaniny.

-Množstvo krviniek v 1 kubickom centimetri.

-Hovory za minútu na telefónnu výmenu.

-Čokoládové iskry prítomné v 1 kg koláčového cesta.

-Počet stromov infikovaných cestou v 1 hektári lesa.

Všimnite si, že tieto náhodné premenné predstavujú počet násobku udalosti, ktorá sa stane na pevné časové obdobie (Hovory za minútu na telefónnu výmenu) alebo danú oblasť priestoru (Defekty tkaniny na meter štvorcový).

Môže vám slúžiť: Proporcionálna variácia

Tieto udalosti, ako už bolo stanovené, sú nezávislé od času, ktorý prešiel od posledného výskytu.

Blížiaci sa k binomickému rozloženiu s distribúciou Poissona

Poissonova distribúcia je dobrým prístupom k binomickému rozdeleniu, pokiaľ:

-Veľkosť vzorky je veľká: n ≥ 100

-Pravdepodobnosť P je malé: p ≤ 0,1

- μ byť v poradí: NP ≤ 10

V takýchto prípadoch je Poissonova distribúcia vynikajúcim nástrojom, pretože binomické rozdelenie môže byť komplikované v týchto prípadoch.

Vyriešené cvičenia

Cvičenie 1

Seizmologická štúdia zistila, že počas posledných 100 rokov bolo na celom svete 93 veľkých zemetrasení, najmenej 6.0 v Richter -Logaritmickej stupnici-. Predpokladajme, že Poissonova distribúcia je v tomto prípade primeraným modelom. Nájsť:

a) Priemerný výskyt veľkých zemetrasení ročne.

b) Áno P (y) Je to pravdepodobnosť, že sa bude diať a Zemetrasenia pre náhodný vybraný rok, nájdite nasledujúce pravdepodobnosti:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) a P (7).

c) Skutočné výsledky štúdie sú nasledujúce:

- 47 rokov (0 zemetrasení)

- 31 rokov (1 zemetrasenia)

- 13 rokov (2 zemetrasenia)

- 5 rokov (3 zemetrasenia)

- 2 roky (4 zemetrasenia)

-  0 rokov (5 zemetrasení)

- 1 roky (6 zemetrasení)

- 1 roky (7 zemetrasení)

Ako sú tieto výsledky s výsledkami získanými v pododdiele B? Je Poissonova distribúcia dobrou voľbou na modelovanie týchto udalostí?

Riešenie do)

a) Zemetrasenia sú udalosti, ktorých pravdepodobnosť p Je malý a uvažujeme o obmedzenom časovom období, jedného roka. Priemerné zemetrasenia sú:

μ = 93 /100 zemetrasení / rok = 0.93 zemetrasení ročne.

Riešenie b)

b) Na výpočet požadovaných pravdepodobností sa hodnoty nahradia vo vzorci uvedenom na začiatku:

Napríklad nájsť P (2), čo by bola pravdepodobnosť, že ročne budú 2 veľké zemetrasenia:

y = 2

μ = 0.93

E = 2.71828

A to je pravdepodobnosť, že na rok existuje 7 veľkých zemetrasení:

Je to dosť menej ako p (2).

Výsledky sú uvedené nižšie:

P (0) = 0.395, p (1) = 0.367, p (2) = 0.171, p (3) = 0.0529, p (4) = 0.0123, p (5) = 0.00229, p (6) = 0.000355, p (7) = 0.0000471.

Napríklad by sme mohli povedať, že existuje pravdepodobnosť 39.5 %, že v danom roku nevyskytuje žiadne veľké zemetrasenie. Alebo že existuje 5,29 %, v ktorom sa v tom roku vyskytujú 3 veľké zemetrasenia.

Riešenie c)

c) Frekvencie sa analyzujú a vynásobia sa n = 100 rokov:

39.5; 36.7; 17.1; 5.29; 1.23; 0.229; 0.0355 a 0.00471.

Môže vám slúžiť: algebraické deriváty

Napríklad:

- Frekvencia 39.5 naznačuje, že v 39.Vyskytujú sa 5 zo 100 rokov alebo veľké zemetrasenia, mohli by sme povedať, že je celkom blízko k skutočnému 47 -ročnému výsledku bez veľkého zemetrasenia.

Porovnajme ďalší výsledok Poissona so skutočnými výsledkami:

- Hodnota získaná z 36.7 znamená, že v 37 -ročnom období je 1 veľké zemetrasenie. Skutočným výsledkom je, že za 31 rokov došlo k 1 veľkému zemetraseniu, dobrá zhoda s modelom.

- 17 sa očakáva.1 roky s 2 veľkými zemetraseniami a je známe, že za 13 rokov, čo je blízka hodnota, boli v skutočnosti 2 veľké zemetrasenia.

Preto je Poissonový model prijateľný v tomto prípade.

Cvičenie 2

Spoločnosť odhaduje, že počet komponentov, ktoré zlyhajú pred dokončením 100 hodín prevádzky, sleduje Poissonovu distribúciu. Ak je priemerný počet zlyhaní v tom čase 8, nájdite nasledujúce pravdepodobnosti:

a) že komponent zlyhá za 25 hodín.

b) Porucha menej ako dve komponenty za 50 hodín.

c) že najmenej tri komponenty zlyhajú za 125 hodín.

Riešenie do)

a) Je známe, že priemerná chyba za 100 hodín je 8, preto sa očakáva za 25 hodín, štvrtá časť zlyhaní, to znamená 2 zlyhania. Toto bude parameter μ.

Pravdepodobnosť zlyhania 1 komponentu sa požaduje, náhodná premenná je „komponenty, ktoré zlyhajú pred 25 hodinami“ a jej hodnota je y = 1. Nahradením funkcie pravdepodobnosti:

 b) Teraz je náhodná premenná „komponenty, ktoré zlyhajú pred 50 hodinami“. Parameter je μ = 4, Pretože očakávaná hodnota zlyhaní za 50 hodín je 4.

Otázkou však je pravdepodobnosť, že menej ako dve zložky zlyhajú za 50 hodín, nie že presne 2 komponenty zlyhajú za 50 hodín, preto musíme pridať pravdepodobnosti, že:

-Žiadne zlyhá

-Zlyhajte iba 1

P (menej ako 2 komponenty) = p (0) + p (1)

P (menej ako 2 komponenty) = 0.0183+0.0732 = 0.0915

c) že najmenej 3 komponenty zlyhajú v roku 125, to znamená, že v tom čase môže zlyhať 3, 4, 5 alebo viac.

Pravdepodobnosť, ktorá nastane aspoň jedna z niekoľkých udalostí, sa rovná 1, s výnimkou pravdepodobnosti, že sa k žiadnym udalostiam nestane.

-Vyžiadanú udalosť je zlyhať 3 alebo viac komponentov za 125 hodín

-To, že sa udalosť nestane, znamená, že zlyhávajú menej ako 3 komponenty, ktorých pravdepodobnosť je: P (0)+p (1)+p (2)

Parameter μ v tomto prípade je:

 μ = 8 + 2 = 10 porúch za 125 hodín.

P (padlé 3 alebo viac komponentov) = 1- p (0)- p (1)- p (2) =

= 1-0.0026786 = 0.9972

Odkazy

1. Matematika. Poisson Distribúcia. Obnovené z: je.Matematika.com
2. Mendenhall, W. 1981. Štatistiky pre správu a ekonomiku. Tretí. vydanie. Redakčná skupina Iberoamerica.
3. Trek. Naučte sa štatistiky. Poisson Distribúcia. Obnovené z: stattrek.com,
4. Triola, m. 2012. Štatistika. 11. Edimatizovať. Pearson Vzdelanie.
5. Wikipedia. Poisson Distribúcia. Zdroj: In.Wikipedia.orgán