Vzorce korelačných koeficientov, výpočet, interpretácia, príklad

On korelačný koeficient V štatistike je to indikátor, ktorý meria trend dvoch kvantitatívnych premenných x a y, aby medzi nimi mali vzťah linearity alebo proporcionality.

Všeobecne platí, že páry premenných x a y sú dve charakteristiky rovnakej populácie. Napríklad X môže byť výška osoby E a jej hmotnosť.

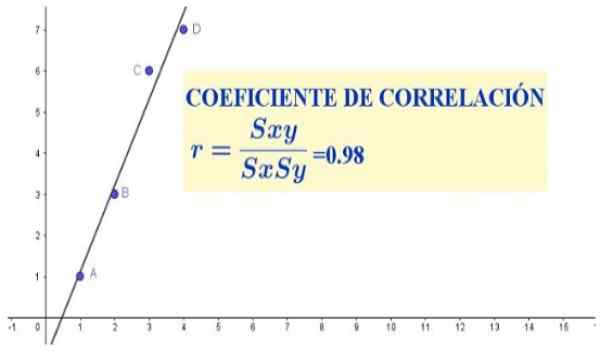
postava 1. Korelačný koeficient pre štyri páry dát (x, y). Zdroj: f. Zapata.

V tomto prípade by korelačný koeficient naznačil, či existuje pomer proporcionality medzi výškou a hmotnosťou danej populácie.

Pearsonov lineárny korelačný koeficient je označený listom r malé písmená a jeho minimálne a maximálne hodnoty sú -1 a +1. 

Hodnota r = +1 by naznačovala, že celé páry (x, y) sú dokonale zarovnané a že keď X rastie a bude rásť v rovnakom pomere. Na druhej strane, ak sa stane, že r = -1, sada párov by bola tiež dokonale zarovnaná, ale v takom prípade, keď X rastie, a zníži sa v rovnakom pomere.

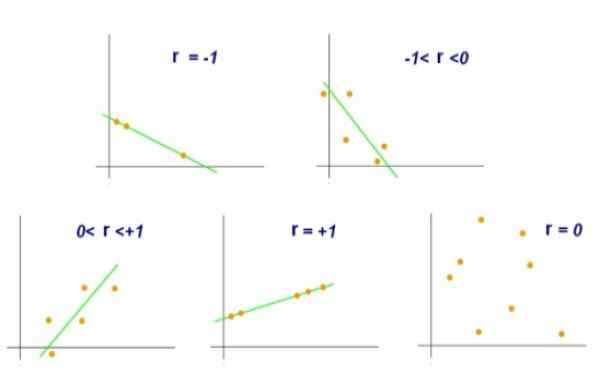Obrázok 2. Rôzne hodnoty korelácie lineárnej korelácie. Zdroj: Wikimedia Commons.

Na druhej strane, hodnota r = 0 by naznačovala, že medzi premennými x a y neexistuje žiadna lineárna korelácia. Zatiaľ čo hodnota r = +0,8 by naznačovala, že páry (x, y) majú tendenciu zoskupovať sa na jednu stranu a druhú z určitej línie.

Vzorec na výpočet korelačného koeficientu R je nasledujúci:

Kde čitateľ predstavuje kovarianciu medzi premennými x a y, zatiaľ čo menovateľ je produktom štandardnej odchýlky pre premennú x a štandardnú odchýlku pre premennú a.

Ako vypočítať korelačný koeficient?

Lineárny korelačný koeficient je štatistické množstvo, ktoré je začlenené do vedeckých kalkulačiek, vo väčšine tabuliek a štatistických programov.

Môže vám slúžiť: Hyperbolický paraboloid: Definícia, vlastnosti a príklady

Je však vhodné vedieť, ako sa uplatňuje vzorec, ktorý sa definuje, a na tento.

A ako je uvedené v predchádzajúcej časti, korelačným koeficientom je kovariancia SXY vydelená produktom štandardnej odchýlky SX pre premenné x a Sy pre premennú a.

Kovariancia a rozptyl

SXY kovariancia je:

Sxy = [σ (xi -) (yi -)] / (n -1)

Kam je suma od 1 do N párov (xi, yi). E sú aritmetické pančuchy údajov xi e yi.

Pokiaľ ide o svoju časť, štandardná odchýlka pre premennú x je odmocninou rozptylu súboru údajov XI, s I od 1 do N:

Sx = √ [σ (xi -)^2) / (n -1)]

Podobne štandardná odchýlka pre premennú a je odmocninou rozptylu súboru údajov YI, s I od 1 do n:

SY = √ [σ (yi -)² ) / (N-1)]

Ilustratívny prípad

Aby sme podrobne ukázali spôsob výpočtu korelačného koeficientu, vezmeme nasledujúcu sadu štyroch párov údajov 

(X, y): (1, 1); (23); (3, 6) a (4, 7).

Najprv vypočítame aritmetický priemer pre x a y nasledovne:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Potom sa vypočítajú zostávajúce parametre:

Kovariancia SXY

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Môže vám slúžiť: pravidlá odvodenia (s príkladmi)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Štandardná odchýlka SX

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Štandardná odchýlka

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Koeficient zábradlia r

R = 3.5 / (1.29 * 2.75) = 0.98

Interpretácia

V súbore údajov v predchádzajúcom prípade je silná lineárna korelácia medzi premennými X a Y, ktorá sa prejavuje v disperznom grafe (ktorý je vidieť na obrázku 1), ako aj v korelačnom koeficiente, ktorý hodil hodnotu celkom blízko jednotka.

Pokiaľ je korelačný koeficient bližšie k 1 alebo -1, väčší zmysel robí nastavenie údajov na čiaru, výsledok lineárnej regresie.

Lineárna regresia

Lineárna regresná čiara sa získa z Spôsob najmenších štvorcov. v ktorom sa parameter regresnej čiary získava z minimalizácie súčtu štvorca rozdielu medzi hodnotou a odhadovanou hodnotou a YI dátových údajov.

Na druhej strane parametre A a B regresnej čiary y = a + bx, získané metódou minimálnych štvorcov, sú:

*B = sxy / (sx²) Pre svah

*A = - b pre križovatku regresnej čiary s osou a.

Pripomeňme, že SXY je kovariancia definovaná vyššie a SX² Je to rozptyl alebo štvorec štandardnej odchýlky predtým definovanej. E sú aritmetické prostriedky údajov X a respektíve.

Príklad

Korelačný koeficient sa používa na určenie, či existuje korelácia lineárneho typu medzi dvoma premennými. Je použiteľné, keď sú premenné, ktoré sa majú študovať.

Môže vám slúžiť: korešpondenčné pravidlo funkcie

Ilustratívny príklad, ktorý máme nižšie: Miera stupňa obezity je index telesnej hmotnosti, ktorý sa získa vydelením hmotnosti jednej osoby na kilogramy medzi výškou jej v štvorcových jednotkách k štvorcovi.

Je potrebné vedieť, či existuje silná korelácia medzi indexom telesnej hmotnosti a koncentráciou HDL cholesterolu v krvi, meraná v milimolách na liter. Na tento účel sa uskutočnila štúdia s 533 ľuďmi zhrnuté v nasledujúcom grafe, v ktorom každý bod predstavuje údaje osoby.

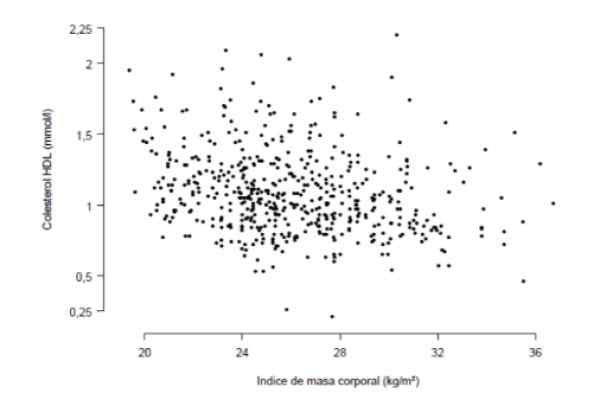Obrázok 3. Štúdia IMC a HDL cholesterol u 533 pacientov. Zdroj: Aragonský inštitút zdravotníckych vied (IACS).

Z starostlivého pozorovania grafu vyplýva, že medzi koncentráciou HDL cholesterolu a indexom telesnej hmotnosti existuje určitý lineárny (nie príliš výrazný) trend medzi koncentráciou cholesterolu HDL a indexom telesnej hmotnosti. Kvantitatívne meranie tohto trendu je korelačný koeficient, ktorý sa v tomto prípade ukázal ako r = -0 276.

Odkazy

1. González C. Všeobecná štatistika. Získané z: Tarwi.La Molina.Edu.pešo
2. IACS. Aragonský inštitút zdravotníctva vied. Zdroj: ICS-Aragon.com 
3. Salazar C. a Castillo S. Základné štatistické zásady. (2018). Zdroj: DSPACE.Uce.Edu.ES
4. Superprof. Korelačný koeficient. Obnovené z: Superprof.je
5. Usac. Príručka pre opisnú štatistiku. (2011). Získané z: Štatistiky.inžinierstvo.Usac.Edu.Gt
6. Wikipedia. Pearsonov korelačný koeficient. Obnovené z: je.Wikipedia.com.