Rozdiely medzi rýchlosťou a rýchlosťou (s príkladmi)

Ten Rozdiely medzi rýchlosťou a rýchlosťou Existujú, hoci obe sú súvisiace fyzické množstvá. V bežnom jazyku sa jeden alebo druhý termín alebo druhý používa zameniteľne, akoby boli synonymom, ale vo fyzike je potrebné ich rozlíšiť.

V tomto článku sú definované oba koncepty, rozdiely sú uvedené a vysvetlené príkladmi, ako a kedy sa vzťahuje jeden alebo druhý. Aby sme zjednodušili, uvažujeme o pohyblivej častice a odtiaľ preskúmame koncepty rýchlosti a rýchlosti. 

	Rýchlosť	Rýchlosť
Definícia	Je to vzdialenosť prejdená na jednotku času.	Je posun (alebo zmena polohy) v každej jednotke času.
Notácia	vložka	vložka
Typ matematického objektu	Vyliezť.	Vektor.
Vzorec (na konečné časové obdobie)*	v = ΔS/Δtón	v = ΔR/Δtón
Vzorec (na okamih daného času) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Vysvetlenie vzorca	*Dĺžka cesty prejdená rozdelenou medzi časové obdobie, ktoré sa používa na jej cestovanie.** V okamžitej rýchlosti má časové rozpätie tendenciu k nule. ** Matematická operácia je derivátom trajektórie oblúka ako funkcia času vzhľadom na čas t.	*Vektorový posun vydelený časovým obdobím, v ktorom došlo k posunu. ** Pri okamžitej rýchlosti má časové obdobie tendenciu k nule. ** Matematická operácia je derivátom pozície včas.
Charakteristika	Na jeho vyjadrenie je potrebné iba pozitívne skutočné číslo, bez ohľadu na priestorové rozmery, v ktorých sa pohyb vyskytuje. ** Okamžitá rýchlosť je absolútna hodnota okamžitej rýchlosti.	Na jeho vyjadrenie môže byť potrebné viac ako jedno skutočné číslo (pozitívne alebo negatívne) v závislosti od priestorových rozmerov, v ktorých sa pohyb uskutočňuje. ** Modul okamžitého rýchlosti je okamžite.

Príklady s jednotnou rýchlosťou v priamých častiach

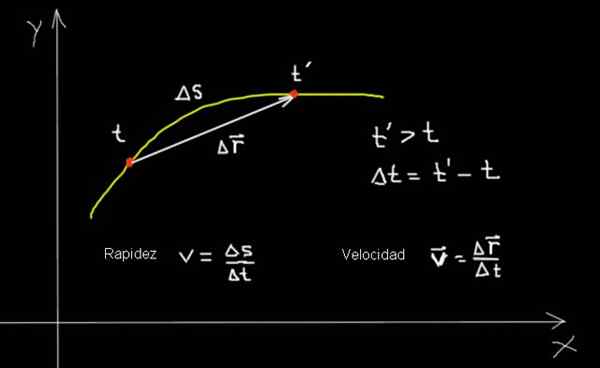
Rýchlosť a rýchlosť častice, ktorá sa pohybuje v krivke. Pripravený: f. Zapata.

V predchádzajúcej tabuľke bolo zhrnutých niekoľko aspektov rýchlosti a rýchlosti. A potom sa dopĺňajú niekoľko príkladov, ktoré ilustrujú zapojené pojmy a ich vzťahy:

Môže vám slúžiť: paramagnetizmus

- Príklad 1

Predpokladajme, že červený mravec sa pohybuje po priamke a v smere uvedenom na nasledujúcom obrázku.

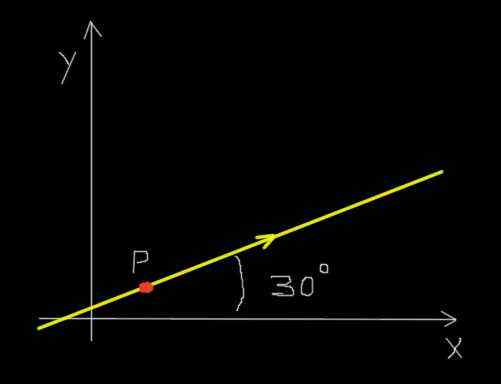Mravec na rektilineálnej ceste. Zdroj: f. Zapata.

Okrem toho sa mravec pohybuje rovnomerne tak, aby prešiel vzdialenosťou 30 milimetrov v časovom období 0,25 sekundy. 

Určiť rýchlosť a rýchlosť mravca.

Riešenie 

Rýchlosť mravca sa vypočíta vydelením vzdialenosti ΔS Toure Tour Δt.

V = ΔS/At = (30 mm)/(0,25 s) = 120 mm/s = 12 cm/s

Rýchlosť mravca sa vypočíta vydelením posunu Δr Medzi časovým obdobím, v ktorom sa uskutočnilo uvedené vysídlenie.

Posun bol 30 mm v smere 30 ° vzhľadom na os x alebo v kompaktnej forme: 

Δr = (30 mm ¡30 °)

Dá sa poznamenať, že posun pozostáva z veľkosti a adresy, pretože je to vektorové množstvo. Alternatívne je možné posunutie vyjadriť podľa svojich karteziánskych komponentov X a Y týmto spôsobom:

Δr = (30 mm* cos (30 °); 30 mm* bez (30 °)) = (25,98 mm; 15,00 mm)

Miera mravca sa vypočíta vydelením posunu medzi časové obdobie, v ktorom bola vykonaná:

vložka = Δr/Δt = (25,98 mm / 0,25 s; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Táto rýchlosť v karteziánskych komponentoch X a Y Y v jednotkách CM/S je:

v = (10 392; 6 000) cm/s.

Alternatívne môže byť rýchlostný vektor vyjadrený vo svojej polárnej forme (smer modulu), ako je znázornené:

vložka = (12 cm/s ¡30 °).

Poznámka: V tomto príklade, pretože rýchlosť je konštantná, sa priemerná rýchlosť a okamžitá rýchlosť zhodujú. Je dokázané, že okamžitý rýchlostný modul je okamžitý rýchly.

Môže vám slúžiť: hustota

Príklad 2

Rovnaký mravec z predchádzajúceho príkladu prechádza z A na B, po B na C a nakoniec z C na A, sleduje trojuholníkovú dráhu znázornenú na nasledujúcom obrázku.

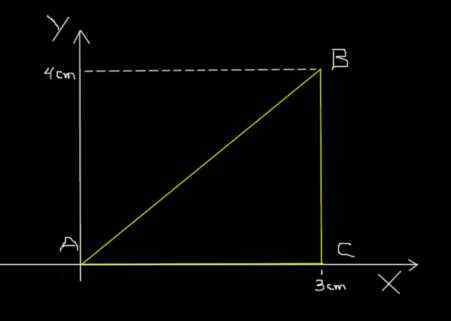Trojuholníková cesta mravca. Zdroj: f. Zapata.

Sekcia AB cestuje pri 0,2 s; BC cestuje pri 0,1 s a nakoniec CA cestuje pri 0,3 s. Vypočítajte priemernú rýchlosť trasy ABCA a priemernú rýchlosť trasy ABCA.

Riešenie 

Na výpočet priemernej rýchlosti mravca začneme stanovením celkovej prejdenej vzdialenosti:

Δs = 5 cm + 4 cm + 3 cm = 12 cm.

Časové obdobie používané na celú cestu je:

Δt = 0,2 s + 0,1 s + 0,3 s = 0,6 s.

Priemerná rýchlosť mravca je teda:

V = ΔS/At = (12 cm)/(0,6 s) = 20 cm/s.

Potom sa vypočíta priemerná rýchlosť mrace na trase ABCA. V tomto prípade je posunutie vykonané mravcom:

ΔR = (0 cm; 0 cm)

Dôvodom je skutočnosť, že posun je rozdiel medzi konečnou polohou menej počiatočnou polohou. Pretože obe pozície sú rovnaké, potom je ich rozdiel neplatný, čo je výsledkom nulového posunu.

Toto nulové posunutie sa uskutočňovalo v časovom období 0,6 s, takže priemerný typ mravca bol:

vložka =(0 cm; 0 cm)/ 0,6S = (0; 0) cm/ s.

Záver: Priemerná rýchlosť 20 cm/s, Ale priemerná rýchlosť je na trase ABCA nula nula.

Príklady s jednotnou rýchlosťou na zakrivených úsekoch

Príklad 3

Hmyz sa pohybuje na kruhu polomeru 0,2 m s rovnomernou rýchlosťou, takže začínajúc od A a dosiahnutia B, cestuje ¼ obvodu po 0,25 s.

Môže vám slúžiť: hydraulický lis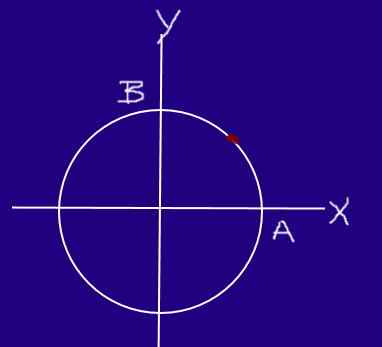Hmyz. Zdroj: f. Zapata.

Určte rýchlosť a rýchlosť hmyzu v sekcii AB.

Riešenie 

Dĺžka obvodu obvodu medzi A a B je:

Δs = 2πr /4 = 2π (0,2 m) /4 = 0,32 m.

Uplatňovanie definície priemernej rýchlosti, ktorú máte:

V = ΔS/At = 0,32 m/0,25 s = 1,28 m/s.

Na výpočet priemernej rýchlosti je potrebné vypočítať vektor posunu medzi počiatočnou polohou A a konečným B:

Δr = (0; r)-(r; 0) = (-r; r) = (-0,2; 0,2) m

Uplatňovanie priemernej definície rýchlosti sa získa:

vložka = Δr/ Δt = (-0,2; 0,2) m / 0,25 s = (-0.8; 0,8) m/s.

Predchádzajúci výraz je priemerná rýchlosť medzi A a B vyjadrená v karteziánskej podobe. Alternatívne je možné priemernú rýchlosť vyjadriť v polárnej forme, to znamená modul a smer:

| vložka | = ((-0,8)^2 + 0,8^2)^(½) = 1,13 m/s

Adresa = Arctan (0,8 / (-0,8)) = arcan (-1) = -45 ° + 180 ° = 135 ° vzhľadom na os x.

Nakoniec je priemerná rýchlostná vektor v polárnej forme: vložka =(1,13 m/s ¡135 °).

Príklad 4

Za predpokladu, že počiatočný moment hmyzu predchádzajúceho príkladu je 0S z bodu A, vaša vektorová poloha je v okamihu, keď sa dá daný:

r(t) = [r cos ((π/2) t); R sen ((π/2) t)].

Stanovte rýchlosť a okamžitú rýchlosť pre akýkoľvek okamih t.

Riešenie 

Okamžitá rýchlosť je derivát vzhľadom na čas polohy:

vložka(t) = dr/dt = [-r (π/2) bez ((π/2) t); R (π/2) cos ((π/2) t)]]

Okamžitá rýchlosť je modul okamžitej rýchlosti vektora:

v (t) = | vložka(T) | = π r / 2^½

Odkazy

1. Alons m., Finn e. Fyzika Zväzok I: Mechanika. 1970. Inter -American Educational Fund S.Do.
2. Hewitt, P. Koncepčná fyzická veda. Piaty vydanie. Pearson.
3. Mladý, Hugh. Fyzika univerzity s modernou fyzikou. 14. vydanie. Pearson.
4. Wikipedia. Rýchlosť. Obnovené z: je.Wikipedia.com
5. Zita, a. Rozdiel medzi rýchlosťou a rýchlosťou. Zdroj: diferenciátor.com