Domovská stránka
Fyzický
Elektrické vedenie prúdu a príklady prúdu

Fyzický

Elektrické vedenie prúdu a príklady prúdu

1629
216
Tomáš Klapka

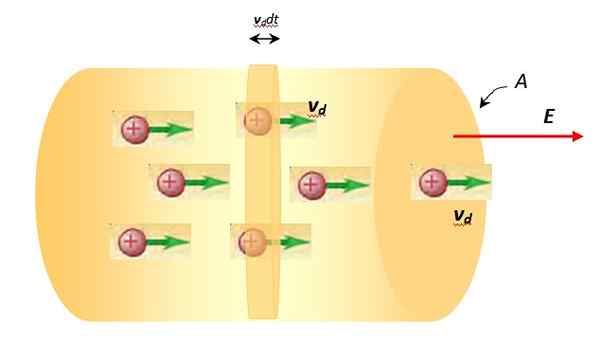
To sa nazýva súčasná hustota do množstva prúdu na jednotku plochy prostredníctvom vodiča. Je to vektorová veľkosť a jeho modul je daný kvocientom medzi okamžitým prúdom a ktorý prechádza prierezom vodiča a jeho plochou S, takže:

$J=\fracIS$ Smer vektora prúdovej hustoty je smer normálneho vektora jednotky do prierezu n a nakoniec smer je rovnaký ako prúd, ktorý sa na základe konvencie berie ako ten, ktorý by mali nosiče pozitívneho zaťaženia.

Týmto spôsobom sú jednotkami v medzinárodnom systéme pre vektor hustoty prúdu AMP na meter štvorcový: A/M². Vektorovo hustota prúdu je:

$\vecJ=\fracIA\hatn$ Na obrázku nižšie je vektor prúdovej hustoty, ktorého veľkosť je v tomto prípade J (y, z), to znamená súradnicová funkcia J, a, a z. S je prierezová oblasť, ktorá je ilustrovaná štvorcová, ale môže mať akúkoľvek inú formu, zvyčajne je kruhová.

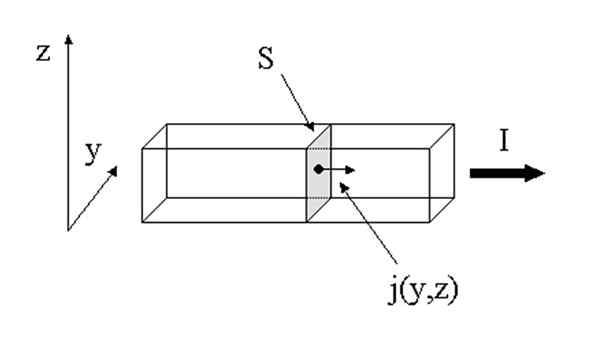Vektor hustoty prúdu. Zdroj: Wikimedia Commons.

Hustota prúdu a intenzita prúdu sú príbuzné, hoci prvý je vektor a druhý nie je. Prúd nie je vektorom napriek tomu, že má veľkosť a význam, pretože mať preferenčný smer vo vesmíre nie je potrebný na vytvorenie koncepcie.

Elektrické pole zriadené vo vnútri vodiča je však vektor a súvisí so prúdom. Je intuitívne chápané, že pole je intenzívnejšie, keď je prúd tiež intenzívnejší, ale prierez vodiča tiež v tomto aspekte hrá určujúcu úlohu.

[TOC]

Elektrický vodičský model

V kuse neutrálneho vodivého drôtu, ako je ten, ktorý je znázornený na obrázku 3, valcovým spôsobom. V rámci vodiča, podľa typu látky, ktorú je vyrobený, bude n nosiče na objem jednotky. Toto n by sa nemalo zamieňať s normálnym vektorom kolmým na vodivý povrch.

Kus valcovitého vodiča ukazuje vo vnútri súčasných nosičov, ktoré sa pohybujú rôznymi smermi. Zdroj: Self Made.

Navrhovaný model materiálu správania pozostáva z pevnej iónovej siete a elektrónového plynu, ktoré sú súčasnými nosičmi, aj keď sú tu zastúpení so znakom A +, pretože ide o kongres pre súčasný.

Čo sa stane, keď sa ovládač pripojí k batérii?

Potom je vytvorený potenciálny rozdiel medzi koncami vodiča vďaka zdroju, ktorý je zodpovedný za prácu: batéria.

Môže vám slúžiť: nebeské telá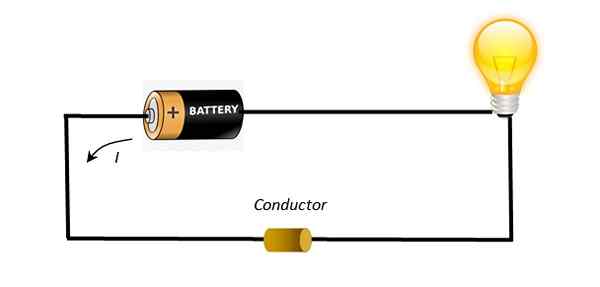

Jednoduchý obvod zobrazuje batériu, ktorá pomocou vodičov vodiča zapína žiarovku. Zdroj: Self Made.

Vďaka tomuto potenciálnemu rozdielu súčasní dopravcovia zrýchľujú a pochodujú riadnejším spôsobom, ako keď bol materiál neutrálny. Týmto spôsobom ste schopní zapáliť žiarovku zobrazeného obvodu.

V tomto prípade bolo vo vnútri vodiča vytvorené elektrické pole, ktoré sa zrýchľuje na elektróny. Cesta ich samozrejme nie je voľná: hoci elektróny majú zrýchlenie, keď sa zrážajú s kryštalickou siete, vzdajú sa časti svojej energie a neustále sa rozptýlia. Globálnym výsledkom je, že sa pohybujú trochu viac v materiáli, ale určite ich pokrok je veľmi malý.

Keď sa zrážajú s kryštalickou sieťou, spôsobujú, že vibrujú, čo vedie k vykurovaniu vodiča. Toto je efekt, ktorý sa ľahko všimne: vodivé káble sa zahrievajú, keď sú krížené elektrickým prúdom.

**Rýchlosť ťahania vložka_da aktuálna hustota**

Súčasní nositelia majú teraz globálny pohyb rovnakým smerom ako elektrické pole. Táto globálna rýchlosť, ktorú majú, sa volá rýchlosť ani rýchlosť A je symbolizovaný ako vložka_d.

Po vytvorení potenciálneho rozdielu majú súčasní dopravcovia riadnejší pohyb. Zdroj: Self Made.

Môže sa vypočítať pomocou niektorých jednoduchých úvah: vzdialenosť prevezená vo vodičovi pre každú časticu v časovom intervale Dt je vložka_d . Dt. Ako už bolo povedané, existujú n Častice na jednotku objemu, pričom objem je produktom oblasti prierezu A podľa vzdialenosti:

V = a.vložka_d Dt

Ak má každá častica zaťaženie Q, koľko zaťaženia DQ prechádza oblasťou Do V časovom intervale Dt?:

dq = q.n. Do.vložka_d Dt

$\fracdQdt=q.n.A.v_d$

Okamžitý prúd je iba DQ/DT, preto:

A rozdelenie medzi A sa získa súčasným vektorom hustoty J:

J = q.n.vložka_d

Keď je zaťaženie pozitívne, vložka_d je rovnakým smerom ako A a J. Keby zaťaženie bolo negatívne, vložka_d je oproti poľa A, ale J a A Naďalej majú rovnakú adresu. Na druhej strane, aj keď je prúd rovnaký v celom obvode, hustota prúdu nemusí nevyhnutne zostať nezmenená. Napríklad je nižšia v batérii, ktorej plocha prierezu je väčšia ako v hnacích drôtoch, tenšia.

Vodivosť materiálu

Je možné predpokladať, že nosiče záťaže pohybujúce sa vo vodiči a nepretržite sa zrážajú s kryštalickou sieťou, čelia sile, ktorá je proti ich pokroku, druhu trenia alebo disipatívnej sily_d čo je úmerné priemernej rýchlosti, ktorú prenášajú, to znamená rýchlosť ťahania:

Môže vám slúžiť: Výhody a nevýhody trenia

F_d ∝ vložka

F_d = α. vložka_d

Toto je model Drude-Lorentz, ktorý sa vytvoril na začiatku 20. storočia, aby vysvetlil pohyb súčasných nosičov vo vodičovi. Nezohľadňuje kvantové účinky. α je konštanta proporcionality, ktorej hodnota je podľa charakteristík materiálu.

Ak je rýchlosť odporu konštantná, súčet síl pôsobiacich na aktuálneho nositeľa je nula. Druhou silou je sila, ktorú vykonáva elektrické pole, ktorého veľkosť je Fe = q.A:

QE - α. vložka_d = 0

Rýchlosť odporu je možné vyjadriť z hľadiska hustoty prúdu, ak sa pohodlne vymaže:

$q.E-\alpha \fracJnq=0$ Preto:

Odkiaľ:

J = nq²E/α

Konštanty N, Q a a sú zoskupené do jedného hovoru σ, takže sa konečne získa:

J = σA

Ohmov zákon

Hustota prúdu je priamo úmerná elektrickým poľom vytvoreným vo vnútri vodiča. K tomuto výsledku je známy ako Ohmov zákon v mikroskopickej forme alebo miestneho OHM zákona.

Hodnota σ = n.Otázka² / a je konštanta, ktorá závisí od materiálu. Je to o elektrická vodivosť alebo jednoducho vodivosť. Jeho hodnoty sú uvedené v tabuľke pre mnoho materiálov a ich jednotky v medzinárodnom systéme sú zosilňovače/volt x meter (A/V.m), hoci existujú aj iné jednotky, napríklad S/M (siemens na meter).

Nie všetky materiály dodržiavajú tento zákon. Tí, ktorí sú známi ako Ohmické materiály.

V látke s vysokou vodivosťou je ľahké zriadiť elektrické pole, zatiaľ čo v inej s nízkou vodivosťou stojí viac práce. Príklady materiálov s vysokou vodivosťou sú: grafén, striebro, meď a zlato.

Príklady aplikácií

-Vyriešený príklad 1

Nájdite rýchlosť odporu voľných elektrónov v medenom kábele prierezu 2 mm² Keď cez ňu prechádza prúd 3. Meď má 1 hnací elektrón na atóm.

Fakt: Avogadro číslo = 6 023 10²³ častice od Mol; elektrónové zaťaženie -1.6 x 10^-19 C; Hustota meďnatého 8960 kg/m³; Molekulová hmotnosť meďnatého: 63,55 g/mol.

Riešenie

Z J = q.n.vložka_d Veľkosť rýchlosti ťahania sa vymaže: $\vecv_d=\frac\vecJnq$ $v_d=\fracIn.q.A$

$v_d=\fracJn.q$ Na uľahčenie výpočtov, hodnota n, čo je počet nosičov zaťaženia na jednotku objemu, potom sa určí veľkosť j a nakoniec sa všetko nahradí v predchádzajúcom výraze:

Môže vám slúžiť: kategorická premenná: Charakteristiky a príklady

Ako sa rozsvietia svetlá okamžite?

Táto rýchlosť je prekvapivo. Môže trvať elektrón takmer hodinu, kým sa dostane z auta batérie na svetlovú žiarovku.

Našťastie nemusíte čakať tak dlho, kým zapália svetlá. Elektrón na batérii rýchlo tlačí ostatných do vodiča, a tak je elektrické pole stanovené veľmi rýchlo, pretože ide o elektromagnetickú vlnu. Je to narušenie, ktoré sa šíri vo vnútri drôtu.

Elektrónmi dokážu skočiť rýchlosťou svetla atómu k susednému a prúdu začína prúdiť rovnakým spôsobom, ako to voda robí cez hadicu. Kvapky na začiatku hadice nie sú rovnaké ako pri východe, ale je to tiež voda.

-Vyriešený príklad 2

Obrázok zobrazuje dva pripojené vodiče vyrobené z toho istého materiálu. Prúd, ktorý vstupuje zľava do tenšej časti, je 2 až. Tam rýchlosť ťahania elektrónov 8.2 x 10^-4 pani. Za predpokladu, že hodnota prúdu zostáva konštantná a nájdi rýchlosť odporu elektrónov v časti pravej, v m/s.

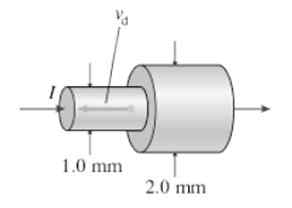
Riešenie

V tenkej časti: J₁ = n.Otázka. vložka_D1 = I/a₁

A v najhrubšej časti: j₂ = n.Otázka. vložka_D2 = I/a₂

Prúd je rovnaký pre obe sekcie, ako aj pre n a Otázka, preto:

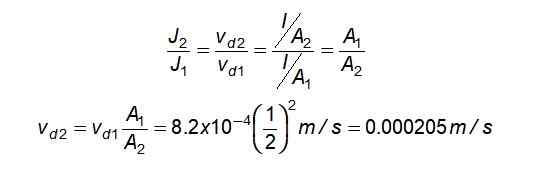Rýchlosť odporu je nižšia v širšej časti, ktorá sa očakávala.