Príklady zoskupených údajov a vyriešené cvičenie

Ten zoskupené údaje Sú to tí, ktorí sa klasifikovali do kategórií alebo tried, pričom ako kritériá považovali za svoju frekvenciu. To sa deje s cieľom zjednodušiť správu veľkých údajov a stanoviť ich trendy.

Po usporiadaní v týchto triedach pre svoje frekvencie, údaje tvoria a Distribúcia frekvencie, z ktorých sa poskytujú informácie o úžitkových informáciách prostredníctvom svojich charakteristík.

postava 1. So zoskupenými údajmi môžete zostaviť grafiku a vypočítať štatistické parametre, ktoré opisujú trendy. Zdroj: Pixabay.

Ďalej uvidíme jednoduchý príklad zoskupených údajov:

Predpokladajme, že sa meria postava 100 študentov, ktorá bola vybraná zo všetkých základných fyzikálnych kurzov univerzity, a získajú sa nasledujúce výsledky:

Získané výsledky boli rozdelené do 5 tried, ktoré sa objavujú v ľavom stĺpci.

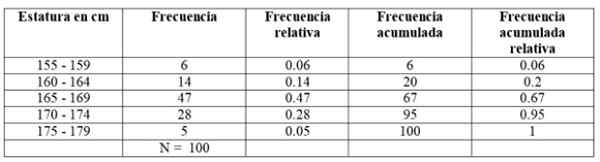
Prvá trieda medzi 155 a 159 cm má 6 študentov, druhá trieda 160 - 164 cm má 14 študentov, tretia trieda od 165 do 169 cm je tá, ktorá má najväčší počet členov: 47. Potom sledujte triedu 170-174 cm s 28 študentmi a nakoniec od 175 do 179 cm s iba 5.

Počet členov každej triedy je presne časť ani Absolútna strava A pridaním všetkých sa získajú celkové údaje, ktoré sú v tomto príklade 100.

[TOC]

Charakteristiky distribúcie frekvencie

Časť

Ako sme videli, frekvencia je počet opakovaní faktu. A na uľahčenie výpočtov distribučných vlastností, ako je priemer a rozptyl, sú definované nasledujúce množstvá:

-Akumulovaná frekvencia: Získava sa pridaním frekvencie triedy s prednou akumulovanou frekvenciou. Prvá zo všetkých frekvencií sa zhoduje s frekvenciou daného intervalu a posledným je celkový počet údajov.

-Relatívna frekvencia: Vypočíta sa vydelením absolútnej frekvencie každej triedy celkovým počtom údajov. A ak sa vynásobíte 100, máte percentuálne percento frekvencie.

Môže vám slúžiť: vektorové funkcie

-Akumulovaná relatívna frekvencia: Je to súčet relatívnych frekvencií každej triedy s predchádzajúcimi akumulovanými. Posledná z akumulovaných relatívnych frekvencií sa musí rovnať 1.

Pre náš príklad sú frekvencie také:

Hranice

Extrémne hodnoty každej triedy alebo intervalu sa nazývajú Limity triedy. Ako vidíme, každá trieda má nižšiu hranicu a jednu väčšiu. Napríklad prvá trieda štúdie o pozíciách má limit menší ako 155 cm a jeden väčší ako 159 cm.

Tento príklad obsahuje limity, ktoré sú jasne definované, je to však možné.

Hranice

Výška je kontinuálna premenná, takže sa dá uvažovať o tom, že prvá trieda sa skutočne začína v roku 154.5 cm, pretože zaokrúhľovaním tejto hodnoty na najbližšie celé číslo sa získa 155 cm.

Táto trieda pokrýva všetky hodnoty až do 159.5 cm, pretože z toho sú postavy zaokrúhlené na 160.0 cm. Postava 159.7 cm už patrí do ďalšej triedy.

Skutočné hranice triedy tohto príkladu sú v CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitúda

Šírka triedy sa získa odpočítaním hraníc. Pre prvý interval nášho príkladu máte 159.5 - 154.5 cm = 5 cm.

Čitateľ môže overiť, že v ostatných intervaloch príkladu je amplitúda tiež výsledkom od 5 cm. Je však pozoruhodné, že distribúcie môžu byť vytvorené s intervalmi rôznej amplitúdy.

Môže vám slúžiť: Pravidlo T: Charakteristiky, takže je to príklady

Značka triedy

Je to stredný bod intervalu a získa sa priemerom medzi hornou hranicou a dolnou hranicou.

Pre náš príklad je značka prvej triedy (155 + 159)/2 = 157 cm. Čitateľ môže overiť, či zostávajúce značky triedy sú: 162, 167, 172 a 177 cm.

Stanovenie značiek triedy je dôležité, pretože sú potrebné na nájdenie aritmetického priemeru a rozptylu distribúcie.

Opatrenia centrálnej tendencie a disperzie pre zoskupené údaje

Najpoužívanejšie miery centrálnej tendencie sú priemerné, stredné a módy a presne opisujú tendenciu údajov zoskupovať sa okolo určitej centrálnej hodnoty.

Polovica

Je to jedno z hlavných ústredných opatrení tendencie. V zoskupených údajoch je možné aritmetický priemer vypočítať pomocou vzorca:

 Kde:

-X je priemer

-F_Jo je frekvencia triedy

-m_Jo Je to značka triedy

-G je počet tried

-n je celkový počet údajov

Stredný

Pre medián musíte identifikovať interval, kde sa nachádza pozorovanie N/2. V našom príklade je toto pozorovanie číslo 50, pretože existuje celkom 100 údajov. Toto pozorovanie je v intervale 165-169 cm.

Potom musíte interpolovať, aby ste našli numerickú hodnotu, ktorá zodpovedá tomuto pozorovaniu, pre ktorú sa používa vzorec:

Kde:

-C = šírka intervalu, kde sa nachádza medián

-B_M = Dolná hranica intervalu, ku ktorému medián patrí

-F_m = množstvo pozorovaní obsiahnutých v strednom intervale

-N/2 = polovica z celkových údajov

-F_BM = Celkový počet pozorovaní pred stredným intervalom

Formovať

Pre módu je identifikovaná modálna trieda, ktorá obsahuje väčšinu pozorovaní, ktorých značka triedy je známa.

Môže vám slúžiť: šesťuholníková pyramída

Rozptyl a štandardná odchýlka

Rozptyl a štandardná odchýlka sú disperzné opatrenia. Ak označíme rozptyl s S² A štandardnej odchýlke, ktorá je odmocninou rozptylu ako S, pre zoskupené údaje, ktoré budeme mať:

A

Cvičenie

Pre distribúciu postavenia vysokoškolských študentov navrhnutých na začiatku vypočítajte hodnoty:

a) priemer

b) médium

c) móda

d) rozptyl a štandardná odchýlka.

Obrázok 2. Pokiaľ ide o veľa hodnôt, ako napríklad výpisy veľkej skupiny študentov, je vhodnejšie zoskupovať údaje do tried. Zdroj: Pixabay.

Roztok

Zostavme nasledujúcu tabuľku, aby sme uľahčili výpočty:

Prostredníctvom výrazu pre priemernú skupinu zoskupenú vyššie:

Výmena hodnôt a priamo vykonávanie súčtu:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Riešenie B

Interval, do ktorého medián patrí, je 165-169 cm, pretože je to najčastejšie interval.

Identifikujme každú z týchto hodnôt v príklade pomocou tabuľky 2:

C = 5 cm (pozri časť Amplitúd)

B_M = 164.5 cm

F_m = 47

N/2 = 100/2 = 50

F_BM = 20

Výmena vo vzorci:

Riešenie c

Interval obsiahnutý vo väčšine pozorovaní je 165-169 cm, ktorého značka triedy je 167 cm.

Riešenie d

Predchádzajúcu tabuľku rozširujeme pridaním ďalších dvoch stĺpcov:

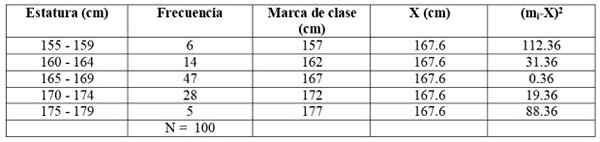
Aplikujeme vzorec:

A vyvíjame sumu:

siež² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Preto:

S = √21.35 cm² = 4.6 cm

Odkazy

1. Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
2. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
3. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
4. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
5. Spiegel, m. 2009. Štatistika. Séria Schaum. 4 ta. Vydanie. McGraw Hill.
6. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.