Distribúcia chí-kvadrát (χ²), ako sa vypočíta, príklady

Dôkaz Štvorcový ani štvorcový (χ², Kde χ je grécky list s názvom „Chi“) sa používa na určenie správania určitej premennej a tiež vtedy, keď chcete vedieť, či sú dve alebo viac premenných štatisticky nezávislé.

Na kontrolu správania premennej, ktorý sa má nazvať testom Chi štvorcový test nastavenia. Vedieť, či sú dve alebo viac premenných štatisticky nezávisle od testu Chi Square nezávislosti, tiež nazývaný kontingencia.

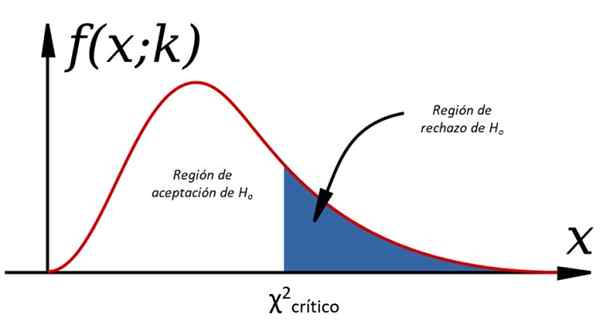
postava 1. Testy hypotézy prostredníctvom Chi Cuadrado

Tieto dôkazy sú súčasťou štatistickej teórie rozhodnutí, v ktorej sa študuje populácia a prijímajú sa o ňom rozhodnutia a analyzujú z nej jednu alebo niekoľko vzoriek extrahovaných z nej extrahovaných. Z tohto dôvodu je potrebné urobiť určité predpoklady týkajúce sa premenných, ktoré sa nazývajú hypotéza, ktoré môžu alebo nemusia byť isté.

Existuje niekoľko testov na porovnanie týchto dohadov a určenie, ktoré sú platné, v rámci určitej marže dôvery, vrátane testu chí-kvadrát, ktorý je možné použiť na porovnanie dvoch a väčšiny populácií.

Ako uvidíme, zvyčajne sa uvažujú dva typy hypotéz o určitom parametri populácie v dvoch vzorkách: nulová hypotéza, nazývaná H_ani (Vzorky sú nezávislé) a alternatívna hypotéza označená ako H₁, (Vzorky sú v korelácii), čo je v rozpore s tým.

[TOC]

Kedy je použitý test chí-kvadrát?

Test Chi Square sa vzťahuje na premenné, ktoré opisujú vlastnosti, ako je pohlavie, občiansky stav, krvná skupina, farba očí a preferencie rôznych typov.

Test je navrhnutý podľa potreby:

-Skontrolujte, či je distribúcia vhodná na opis premennej, ktorá sa nazýva dobrota. Prostredníctvom testu Chi Square môžete vedieť, či existujú významné rozdiely medzi vybraným teoretickým rozdelením a pozorovaným rozdelením frekvencie.

-Vedzte, či sú dve premenné X a Y nezávislé od štatistického hľadiska. Toto je známe ako Test nezávislosti.

Pretože sa vzťahuje na kvalitatívne alebo kategorické premenné, test Chi Square sa široko používa v sociálnych vedách, správe a medicíne.

Podmienky na jeho použitie

Existujú dve dôležité požiadavky na správne použitie:

Môže vám slúžiť: Aký je vzťah medzi oblasťami Rhombus a obdĺžnik?

-Údaje musia byť zoskupené vo frekvenciách.

-Vzorka musí byť dostatočne veľká na to, aby bola distribúcia štvorca Chi platná, inak je jej hodnota nadhodnotená a vedie k odmietnutiu nulovej hypotézy, keď by to tak nebolo.

Všeobecným pravidlom je, že ak sa v zoskupených údajoch objaví frekvencia s hodnotou menšou ako 5, nepoužíva sa. Ak je viac ako jedna frekvencia menšia ako 5, musí sa kombinovať v jednej, aby sa získala frekvencia s číselnou hodnotou vyššou ako 5.

Štvorcová distribúcia

hrebeň² Je to nepretržité rozdelenie pravdepodobností. V skutočnosti existujú rôzne krivky v závislosti od parametra klimatizovať nazývaný stupne slobody náhodne.

Jeho vlastnosti sú:

-Plocha pod krivkou sa rovná 1.

-Hodnoty χ² Sú pozitívne.

-Distribúcia je asymetrická, to znamená, že má zaujatosť.

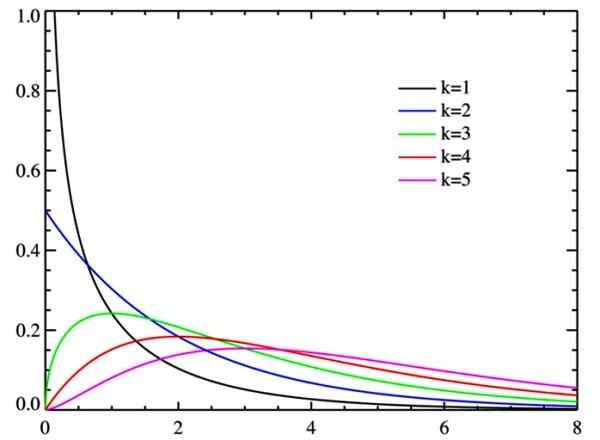Obrázok 2. Chi štvorcová distribúcia pre Wattsov stupne voľnosti. Zdroj: Wikimedia Commons.

Stupne slobody

Ako sa zvyšuje stupne voľnosti, distribúcia chí-kvadrát má tendenciu k normálu, ako je vidieť na obrázku.

Pre dané rozdelenie sa stupne voľnosti určujú prostredníctvom kontingencia, čo je tabuľka, kde sa zaznamenávajú pozorované frekvencie premenných.

Ak má tabuľka F hodnosti a c stĺpce, hodnota klimatizovať je:

K = (f - 1) ⋅ (c - 1)

Formulácia hypotéz

Keď je test Chi Square nastavený, sú formulované nasledujúce hypotézy:

-H_ani: Premenná X má distribúciu pravdepodobnosti f (x) so špecifickými parametrami a₁, a₂... a a_p

-H₁: X má ďalšie rozdelenie pravdepodobnosti.

Distribúcia pravdepodobnosti, ktorá sa predpokladá v nulovej hypotéze, môže byť napríklad dobre známe normálne rozdelenie a parametre by boli priemerné μ a štandardná odchýlka σ.

Okrem toho sa nulová hypotéza hodnotí s určitou úrovňou významnosti, to znamená miera chyby, ktorá by sa urobila pri jej odmietnutí.

Vo všeobecnosti je táto úroveň stanovená 1 %, 5 % alebo 10 % a čím nižšia je výsledok testu, tým spoľahlivejší.

Môže vám slúžiť: Mumm

A ak sa použije Chi štvorcový test nepredvídaných udalostí, čo, ako sme povedali, slúži na overenie nezávislosti medzi dvoma premennými X a Y, hypotézy sú:

-H_ani: Premenné x a y sú nezávislé.

-H₁: X a y sú závislé.

Opäť je potrebné špecifikovať úroveň významnosti, aby ste pri rozhodovaní poznali mieru chyby.

Ako sa vypočítavajú štatistiky chí-kvadrát?

Štatistika CHI Square sa vypočítava takto:

Symbol ∑ znamená „zhrnutie“, ktorý musíme urobiť o uvedenom zlomkovom výraze.

Suma sa vykonáva od prvej triedy I = 1 do poslednej, ktorá je i = k.

Okrem::

-F_ani Je to pozorovaná frekvencia (pochádza z získaných údajov).

-F_a Je to očakávaná alebo teoretická frekvencia (je potrebné ju vypočítať z údajov).

Prijať alebo odmietnuť nulovú hypotézu sa vypočíta χ² Pre pozorované údaje a porovnanie s hodnotou nazývanou Chi kritický štvorec, čo závisí od stupňov slobody klimatizovať a úroveň významnosti α:

hrebeň²_kritický =  hrebeň²_{K, α}

Ak napríklad chceme vykonať test s úrovňou významnosti 1 %, potom a = 0.01, ak to bude s 5%, potom α = 0.05 a tak ďalej. P, parameter distribúcie, napríklad:

P = 1 - a

Tieto kritické štvorcové hodnoty sú určené tabuľkami, ktoré obsahujú hodnotu akumulovanej oblasti. Napríklad pre k = 1, čo predstavuje 1 stupeň voľnosti a a = 0.05, ekvivalent s p = 1-.05 = 0.95, hodnota χ² Je 3.841.

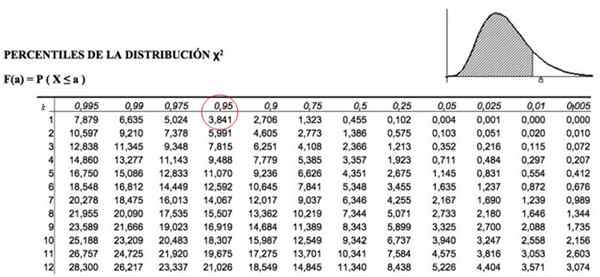Obrázok 3. Tabuľka hodnôt distribúcie štvorcov. Zdroj: f. Zapata.

Kritériá akceptácie AC_ani

Kritériá pre prijatie h_ani je:

-Áno χ² < χ²_kritický  H_ani, inak je odmietnutý (pozri obrázok 1).

Príklad výpočtu

V nasledujúcej aplikácii sa test Chi Square použije ako test nezávislosti.

Predpokladajme, že vedci chcú vedieť, či preferencia čiernej kávy súvisí s žánrom osoby, a špecifikujú odpoveď s úrovňou významnosti a = 0.05.

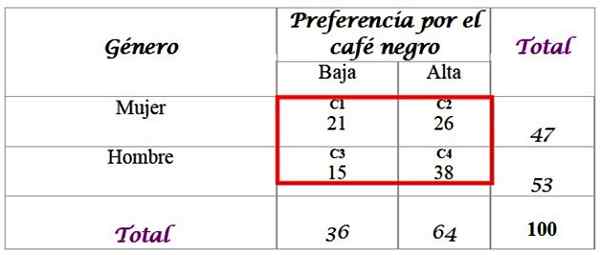
Môže vám slúžiť: externé alternatívne uhly: Cvičenia a cvičenia vyriešené

Z tohto dôvodu sú k dispozícii vzorka 100 ľudí a ich odpovede:

Krok 1

Stanoviť hypotézy:

-H_ani: Pohlavie a preferencie čiernej kávy sú nezávislé.
-H₁: Chuť na čiernu kávu súvisí s žánrom osoby.

Krok 2

Vypočítajte očakávané frekvencie pre distribúciu, pre ktoré sa vyžaduje celková hodnota v poslednom riadku a v pravom stĺpci. Každá bunka v červenej schránke má očakávanú hodnotu F_a, ktorý sa vypočíta vynásobením celkového počtu R riadkov F celkovým stĺpcom C, ktorý je vydelený celkovou vzorkou N:

F_a = (F xc) /n

Výsledky sú nasledujúce pre každú bunku:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Krok 3

Potom musíte vypočítať štatistiku Chi Cuadrado pre túto distribúciu podľa daného vzorca:

hrebeň²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Krok 4

Určiť χ²_kritický, Vedieť, že registrované údaje sú v F = 2 riadkoch a C = 2 stĺpcoch, preto počet stupňov voľnosti je:

K = (2-1) ⋅ (2-1) = 1.

Čo znamená, že sa musíme pozrieť do tabuľky uvedenej vyššie na hodnotu χ²_{K, α} = χ²_{1; 0.05} , ktorý je:

hrebeň²_kritický = 3.841

Krok 5

Porovnajte hodnoty a rozhodnite:

hrebeň² = 2.9005

hrebeň²_kritický = 3.841

Pretože χ² < χ²_kritický Nulová hypotéza je akceptovaná a dospelo sa k záveru, že preferencia čiernej kávy nie je spojená s žánrom osoby s úrovňou významnosti 5%.

Odkazy

1. Chi Square Test pre nezávislosť. Získané z: Saylordotorg.Potápať sa.Io.
2. Vlny. Štatistiky aplikované na zdravotné vedy: test Ji-Square. Získané z: Medwave.Cl.
3. Pravdepodobnosť a štatistika. Shi štvorcový test dobroty. Zdroj: Pravdepodobnosti aestici.com.
4. Triola, m. 2012. Štatistika. 11. Vydanie. Addison Wesley.
5. Žobrák. Štvorcový test. Získané z: Poradenstvo.Cuautitlan2.Žobrák.mx.