Aké sú časti karteziánskeho lietadla?
- 2094
- 180
- JUDr. Rudolf Čapkovič
Ten časti karteziánskeho lietadla Sú zložené z dvoch skutočných kolmých línií, ktoré rozdeľujú karteziánsku rovinu do štyroch regiónov. Každá z týchto regiónov sa nazýva kvadranty a prvky karteziánskeho lietadla sa nazývajú body. Rovina spolu s súradnicovými osami sa volá Karteziánska rovina Na počesť francúzskeho filozofa René Descartes, ktorý vynašiel analytickú geometriu.
Tieto dve čiary (alebo súradnicové osi) sú kolmé, pretože medzi nimi tvoria uhol 90 ° a prechádzajú do spoločného bodu (pôvod). Jedna z riadkov je vodorovná, nazývaná pôvod X (alebo Abcisa) a druhá čiara je vertikálna, nazývaná pôvod Y (alebo usporiadaná).
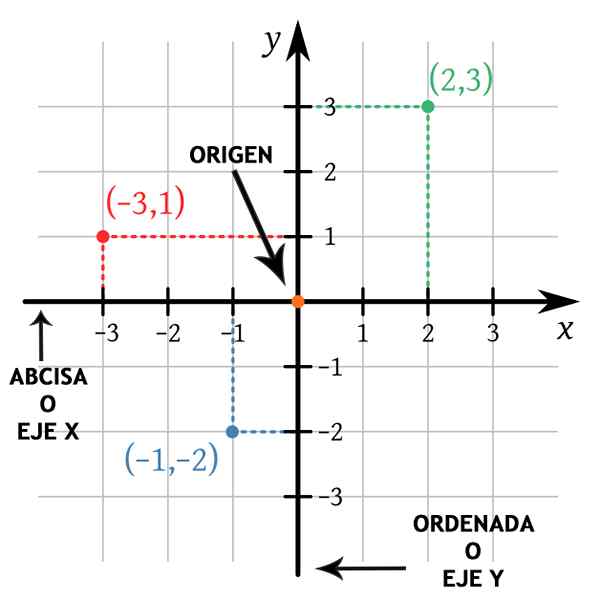 Kbolino / verejná doména
Kbolino / verejná doména Pozitívna polovica os x je napravo od pôvodu a pozitívna polovica osi Y je pôvodom pôvodu. To umožňuje rozlíšiť štyri kvadranty karteziánskej roviny, čo je veľmi užitočné pri grafických bodoch v lietadle.
Karteziánske body
V každom bode P Lietateľovi môže byť pridelené niekoľko skutočných čísel, ktoré sú jej karteziánskymi súradnicami.
Ak prechádza vodorovná čiara a zvislá čiara P, A pretížite sa na x a os do osi y do a b potom súradnice P sú (do,b). Volá sa to (do,b) Dôležitý je usporiadaný pár a poradie, v ktorom sú čísla napísané.
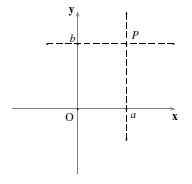
Prvé číslo, do, Je to súradnica v „x“ (alebo Abscissa) a druhom čísle, b, Je to súradnica v „y“ (alebo objednanom). Používa sa notácia P = (do,b).
Je zrejmé, ako bola postavená karteziánska rovina, že pôvod zodpovedá osi „x“ a 0 v osi „y“, to znamená, Ani= (0,0).
Cuadies karteziánskeho lietadla
Ako je vidieť na predchádzajúcich obrázkoch, súradnicové osi generujú štyri rôzne oblasti, ktoré sú kvadrantmi karteziánskej roviny, ktoré sú označené písmenami a, II, III a Iv A tieto sa navzájom líšia v znamení, že body, ktoré sú v každom z nich.
Môže vám slúžiť: algebraické zdôvodnenieKvadrant Jo
Body kvadrantu Jo Sú to tí, ktorí majú obidve súradnice s pozitívnym znamením, to znamená ich súradnice X a ich súradnica a sú pozitívne.
Napríklad bod P = (2,8). Aby som ho získal, bod 2 je umiestnený na osi „x“ a bod 8 na osi „y“, potom sa kreslia vertikálne a vodorovné čiary a kde sa pretína, kde je bod, kde je bod P.
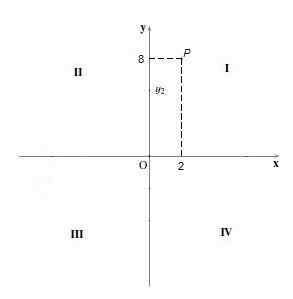
Kvadrant Ii
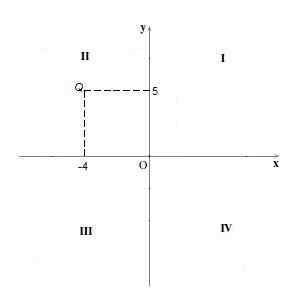
Body kvadrantu Ii Majú svoju negatívnu súradnicu „X“ a pozitívna súradnica „y“. Napríklad bod Q = (-4,5). Je to grafické konanie ako v predchádzajúcom prípade.
Kvadrant Iii
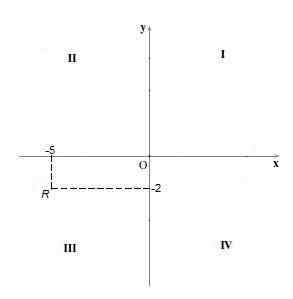
V tomto kvadrante je znamenie oboch súradníc negatívne, to znamená súradnice „x“ a súradnica „y“ sú negatívne. Napríklad bod R = (-5, -2).
Kvadrant Iv
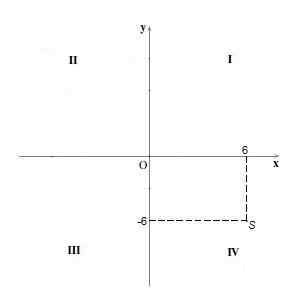
V kvadrante Iv Body majú pozitívnu a koordinovanú „y“ negatívnu súradnicu. Napríklad bod S = (6, -6).

Odkazy
- Fleming, w., & Varberg, D. (1991). Algebra a trigonometria s analytickou geometriou. Pearson Vzdelanie.
- Larson, R. (2010). Predbežný (8 ed.). Učenie sa.
- Lojálny, j. M., & Viloria, n. G. (2005). Plochá analytická geometria. Mérida - Venezuela: Venezuelský redaktor C. Do.
- Oteyza, e. (2005). Analytická geometria (Druhé vydanie.). (G. Tón. Mendoza, ed.) Pearson Education.
- Oteyza, e. d., Osnaya, e. L., Garciadiego, C. H., Hoyo, a. M., & Flores,. R. (2001). Analytická geometria a trigonometria (Prvé vydanie.). Pearson Vzdelanie.
- Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia (Deviate vydanie.). Sála.
- Scott, C. Do. (2009). Geometria karteziánskej roviny, časť: Analytical Conics (1907) (Opakovanie Ed.). Bleskový zdroj.
- « 5 najvýznamnejších jazykových variácií
- Didaktické intervenčné charakteristiky, stratégie, príklady »

