Zachovanie zásady lineárnej momentácie, príklady, cvičenia.

Ten ochrana lineárnej hybnosti tela stanovuje, že produkt jeho hmoty podľa jeho vektora rýchlosti je konštantné množstvo, keď je telo bez interakcie s inými telami a rýchlosťou meranou vzhľadom na pevný alebo neakútny referenčný systém.

Ak existuje niekoľko tiel, ktoré interagujú iba medzi nimi, ale nie s vonkajším prostredím, potom lineárna hybnosť súpravy zostáva v priebehu času konštantný.

Astronaut vo vesmíre je bez akúkoľvek interakciu, preto jeho lineárny moment

Lineárny moment, množstvo lineárneho pohybu alebo jednoducho spád, Je označený listom p A je to vektorová suma:

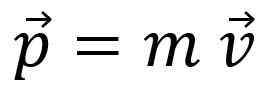
Lineárny moment nie je rovnaký ako rýchlosť, hoci pomer je zrejmý: napríklad kamión, ktorý ide na 20 km/h, má viac lineárneho času ako bicykel, ktorý sa pohybuje rovnakou rýchlosťou.

Aby sa lineárny moment tela zmenil, je potrebné, aby na ňu pôsobila čistá vonkajšia sila, inak zostáva konštantná. Okrem toho lineárny moment P systému vytvoreného pomocou N-telo Je to vektorový súčet jednotlivých okamihov:

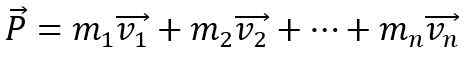
[TOC]

Princíp zachovania množstva lineárneho pohybu

V tele bez síl (alebo v tom, v ktorom sú všetky sily na ňom zrušené) sa stáva, že lineárny moment.

Rovnakým spôsobom prechádza v systéme vytvorenom niekoľkými telami, ktoré interagujú iba navzájom, ale nie s vonkajším prostredím: celkový lineárny moment systému zostáva pevne stanovený počas vývoja množiny súboru.

Tento princíp ochrany je uvedený takto:

Celkový lineárny moment súboru N-tela, ktorý interaguje iba medzi sebou, ale nie s vonkajším prostredím, je nemenným množstvom včas.

A matematicky sa vyjadruje takto:

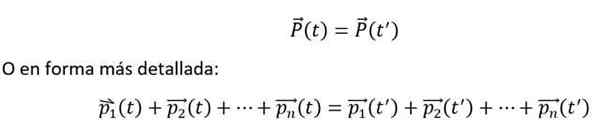
Predchádzajúca rovnosť je splnená, ak a iba vtedy, ak n-Telá interagujú medzi sebou, ale nie s vonkajším prostredím. Okrem toho by sa jednotlivé momenty mali vždy merať vzhľadom na inerciálny referenčný systém.

Príklady

Príklad 1

Dvaja astronauti vo vesmíre sú odobraté z rúk a zostávajú v pevnej polohe vzhľadom na loď. Ale tlačia sa, začnú sa oddeliť v opačných smeroch, keď sú videní z lode.

Môže vám slúžiť: Teória veľkého tresku: Charakteristiky, fázy, dôkazy, problémy

V tomto prípade, pretože interakcia medzi astronaumi je medzi nimi iba prostredníctvom kontaktnej sily ich rúk, celkový lineárny moment. To znamená, celkový lineárny čas 0.

Lineárny moment každého astronauta sa však zmenil. Spočiatku každý mal lineárny moment 0 vzhľadom na loď, ale po tlačení jedného vyjde jedným smerom a druhým v opačnom smere, s nulovými lineárnymi momentmi rovnakej veľkosti a protichodných adries.

Ak sa teda vekerne pridávajú jednotlivé momenty, v dôsledku toho sa získa počiatočná celková lineárna hybnosť.

Na druhej strane, zachovanie lineárneho momentu množstva. Výsledok vynásobenia jej hmoty sa však rovná produktu získaného vynásobením hmotnosti druhého rýchlosťou druhej.

Príklad 2

Šteniatko je na plávajúcej plošine v jazere Calm Waters a jeho majiteľ ju vidí z doku. Na začiatku sú platforma aj šteniatko v pokoji, ale keď sa šteniatko chce priblížiť k majiteľovi, platforma sa pohybuje od doku.

Vysvetlenie tohto pozorovania je presne v zásade zachovania množstva lineárnej hybnosti. Systém pozostáva z šteňa a platformy.

Šteniatko môže chodiť po plošine vďaka trecej sile medzi jej nohami a povrchom, v tomto prípade je trecia sila vnútornou silou interakcie medzi ňou a platformou.

Sada je izolovaný systém a platforma sa môže pohybovať vodorovne po jazere bez všetkého odporu pohybu. Na druhej strane, vo vertikálnom smere sú všetky sily rovnováha a kompenzované a súprava nemá pohyb v tomto smere.

Preto v tejto situácii sú všetky hypotézy splnené tak, aby sa uplatňovala zásada ochrany lineárnej hybnosti.

Príklad 3

Eskimo je ulovený v strede zmrzliny, ľad je taký hladký, že bez ohľadu na to, koľko sa snažil, Eskimo sa pošmykne a vždy zostáva na rovnakom mieste.

Jediným možným spôsobom, ako Eskimo opustí jazero, je to, že leží v smere, v ktorom je ťažký predmet, ktorý sa nesie vo svojom batohu (za predpokladu, že jeden).

Môže vám slúžiť: geometrická optika: aké štúdie, zákony, aplikácie, cvičenia

Žiadosti

Loď

Zachovanie lineárneho momentu. V tomto prípade sa impulz lode dosiahne vyhostením plynov vysokou rýchlosťou, takže raketa sa môže pohybovať opačným smerom, ku ktorému boli vylúčení.

Ak je loď pôvodne v pokoji, keď je palivo spálené a vylúčené, dôjde k sile vyhostenia proti samotnej lodi. Je to vnútorná sila medzi plynmi a loďou. Neexistujú žiadne vonkajšie sily, a preto uplatňuje ochranu lineárneho momentu.

Keďže lineárny moment plynov je rovnaký a na rozdiel od momentu lode, podarí sa mu opustiť odpočinok a tým, že pokračuje v vylúčení plynov, zvyšuje svoje množstvo pohybu, a teda aj jeho rýchlosť.

Každodenný život

Ďalší prípad ochrany lineárneho momentu.

Dalo by sa tvrdiť, že v tomto prípade sa tento princíp nevzťahuje, pretože existuje vonkajšia sila: odpor, ktorý drevo ponúka klincovi.

Avšak v čase kontaktu je sila, ktorú kladivo tlačí na necht, vnútornou silou (medzi systémom, ktorý je klinec a kladivom) oveľa väčšia ako odpor, ktorým je drevo oponované, a preto je zanedbateľná.

Celý lineárny moment kladiva, ktorý je dosť veľký kvôli jeho veľkej hmotnosti a rýchlosti, sa prenáša na necht hneď po zrážke. Všimnite si, že celý moment sa prenáša, ale nie všetka kinetická energia kladiva, pretože jej časť sa transformuje na tepelnú energiu na klinec a kladivo, ktoré po náraze zvyšujú jeho teplotu.

Cvičenia

Cvičenie 1

Andrew a Berenice astronauti sú mimo vesmírnej stanice odobraté z oboch rúk a v pokoji vzhľadom na stanicu. V jazde tlakujú ruky proti vodám druhého a sú prepustení. Ak sa Andrew, 70 kg hmotnosti sa pohybuje pri 1 m/s vzhľadom na stanicu, aká je rýchlosť Berenice so 49 kg hmotnosti?

Riešenie

V tomto prípade sa jasne uplatňuje hypotéza ochrany lineárnej hybnosti, pretože vo vonkajšom priestore nie sú žiadne vonkajšie sily. Sila, s ktorou ich ruky tlačia obidve astronauty, je vnútornou silou.

Môže vám slúžiť: difrakcia vlny: koncept a príklady

Predpokladajme, že Andrewova omša je m_do a to z Berenice m_b. Podobne aj rýchlosti oboch po impulze sú Vložka_do Pre Andrewa a Vložka_b Pre Berenice. Potom sa zachovanie lineárnej hybnosti použije nasledovne:

M_do∙0 + M_b∙0 = M_do∙Vložka_do+ M_b∙Vložka_b

Vyčistenie rýchlosti Berenice máte:

Vložka_b = - (m_do / M_b) ∙ Vložka_do

Umiestnenie numerických hodnôt:

Vložka_b = - (70/49) ∙ (1 m / s) alebo = -1,43 m/s alebo

To znamená, že Berenice sa pohybuje rýchlo 1,43 m/s v opačnom smere Andrewa.

Cvičenie 2

Šteniatko kráča smerom k svojmu majiteľovi na vrchol poloosiatkovej platformy. Zdroj: f. Zapata.

Cesto s 5 kg je v pokoji na platforme 15 kg, ktorá pláva, tiež v pokoji, na jazere Still. Ak šteniatko začne v súvislosti s tým chodiť po plošine rýchlosťou 0,5 m/s. Ako rýchlo bude šteniatko a platforma týkajúce sa pevného pozorovateľa na zem?

Riešenie

Bude sa brať ako inerciálny referenčný systém na dok, kde je majiteľ šteniat. Spočiatku sú šteniatko aj plávajúca plošina v pokoji vzhľadom na dok.

Keď sa šteňa rozhodne rýchlo kráčať smerom k majiteľovi V ' Pokiaľ ide o platformu, platforma sa pohybuje od jari rýchlosťou +Vložka. Rýchlosť šteniatka vzhľadom na dok sa dosahuje vektorovým súčtom svojej rýchlosti vzhľadom na platformu plus rýchlosť platformy a označuje ju:

vložka = -vložka' + Vložka

Pretože odpor vody voči pohybu plošiny je prakticky nulová kvôli jej nízkej rýchlosti, potom je možné potvrdiť, že systém tvorený Šteniatko + platforma Je to izolovaný systém a uplatňuje sa princíp zachovania lineárnej hybnosti:

0 = m ∙ v + m ∙ v

Pamätajte si, že v = v ' + v máte:

0 = -m ∙ v ' + m ∙ v + m ∙ v

To znamená: m ∙ v '= (m+m) ∙ v

Preto v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

Výmena numerických hodnôt je:

V = [5/(5 +15)] ∙ 0,5 m/s = 0,125 m/s

Toto je rýchlosť, s akou sa jarná platforma pohybuje ďalej.

V = -(15/20) ∙ 0,5 m/s = -0,375 m/s

A to je rýchlosť, s akou sa šteňa blíži k doku.

Odkazy

1. Vojvodská univerzita. Systémy častíc. Obnovené z: Webhome.Phy.Vojvoda.Edu.
2. Rex, a. 2011. Základy fyziky. Pearson.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
5. Tipler, P. (2006). Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil.