Konečné súpravy vlastností, príklady, vyriešené cvičenia

Rozumie to Konečná súprava všetky nastavené s obmedzeným alebo účtovným počtom prvkov. Príkladmi konečných súprav sú guličky, ktoré sú obsiahnuté v taške, súbor domov v susedstve alebo v sade P tvorené dvadsiatimi (20) prírodnými číslami:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

Sada vesmírových hviezd je určite obrovská, ale nie je známa, či je konečná alebo nekonečná. Sada planét slnečných systémov je však konečná.

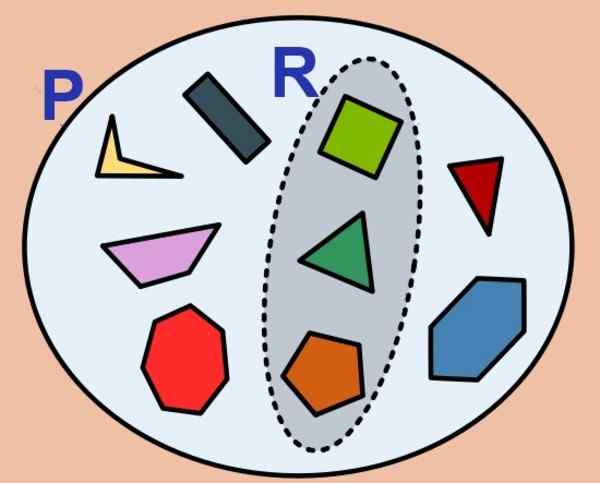
postava 1. Sada polygónov je konečná a podskupina bežných. (Wikimedia Commons)

Počet prvkov konečnej sady sa nazýva jej kardinalita a pre súpravu P Je to označené takto: karta (P) buď #P. Prázdna sada má nulovú kardinalitu a považuje sa za konečnú sadu.

[TOC]

Vlastnosti

Medzi vlastnosťami konečných súborov patrí:

1- Únia konečných súborov výsledky v novej konečnej sade.

2- Ak sa zachytí dve konečné set, je to nová konečná súprava.

3- Podskupina konečnej sady je konečná a jej kardinalita je menšia alebo rovná sa s pôvodnou sadou.

4- prázdna sada je konečná sada.

Príklady

Existuje veľa príkladov konečných súborov. Medzi niektoré príklady patria:

Súbor M z mesiacov v roku, ktoré sa dá rozšíriť takto:

M = Január, február, marec, apríl, máj, jún, júl, august, september, október, november, december, kardinalita M je 12.

Súbor Siež dní v týždni: Siež = Pondelok, utorok, streda, štvrtok, piatok, sobota, nedeľa. Kardinalita S je 7.

Môže vám slúžiť: Vzťahy proporcionality: koncept, príklady a cvičenia

Súbor Ñ Z písmen španielskej abecedy je to konečná súprava, táto sada podľa rozšírenia je napísaná takto:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, O, P, Q, R, S, T, U, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z a jeho kardinalita je 27.

Súbor Vložka Z samohlások v španielčine je to podskupina sady ñ:

Vložka ⊂ Ñ Preto je to konečná súprava.

Konečná súprava Vložka Rozšírený spôsob, ako je napísaný takto: Vložka = a, e, i, o, u a jej kardinalita je 5.

Súpravy môžu byť vyjadrené porozumením. Súbor F Príkladom je písmená slova „konečný“:

F = x / x je písmeno slova „konečné“

Táto sada výrazne vyjadrená bude:

F = f, i, n, t, o, ktorého kardinalita je 5, a preto je to konečná sada.

Viac príkladov

Farby dúhy sú ďalším príkladom konečného súboru, sada C z týchto farieb je:

C = červená, oranžová, žltá, zelená, azúrová, modrá, fialová a jej kardinalita je 7.

Sada fáz F Od Mesiaca je ďalší konečný príklad:

F = New Moon, Growing Room, Full Moon, Waning Room Táto sada má kardinalitu 4.

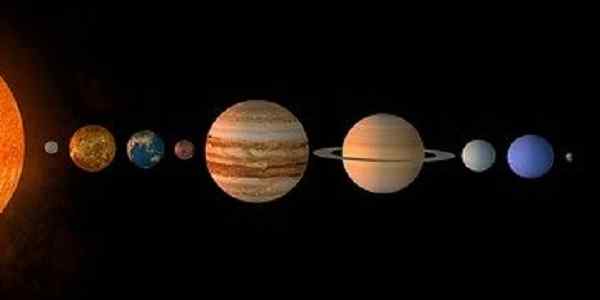Obrázok 2. Planéty slnečnej sústavy tvoria konečnú sadu. (Pixabay)

Ďalšou konečnou sadou je súbor tvorený planétami slnečnej sústavy:

P = Merkúr, Venuša, Zem, Mars, Jupiter, Saturn, Urán, Neptún, Pluto kardinalita 9.

Vyriešené cvičenia

Cvičenie 1

Nasledujúca sada je uvedená a = x∊ r / x^3 = 27. Vyjadrte to slovami a napíšte ich rozšírením, uveďte jej kardinalitu a povedzte, či je alebo nie je konečná.

Môže vám slúžiť: Ellipse

Riešenie: Set A je sada skutočných čísel x tak, že X sa zvýšila na kocku v dôsledku 27.

Rovnica x^3 = 27 má tri riešenia: ktoré sú x1 = 3, x2 = (-3/2 + 3√3/2 i) a x3 = (-3/2-3√3/2 i). Z troch riešení je iba X1 skutočné, zatiaľ čo ďalšie dve sú zložité čísla.

Ako definícia set A hovorí, že X patrí do reálnych čísel, takže riešenia v zložitých číslach nie sú súčasťou súboru.

Rozšírená súprava je:

A = 3, čo je konečná sada kardinality 1.

Cvičenie 2

Symbolicky napíšte (porozumením) a rozsiahle nasadenie B reálnych čísel, ktoré sú väčšie ako 0 (nula) a menej alebo rovné ako 0 (nula). Uveďte svoju kardinalitu a či je alebo nie je konečná.

Riešenie: B = x∊ r / 0 < x <= 0

Sada B je prázdna, pretože skutočné číslo X nemôže byť súčasne väčšie a menšie ako nula, ako aj 0 a tiež menej ako 0.

B = a jej kardinalita je 0. Prázdna súprava je konečná sada.

Cvičenie 3

Sada riešení určitej rovnice je uvedená. Sada porozumením je napísaná takto:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Túto súpravu rozsiahle napíšte, uveďte svoju kardinalitu a uveďte, či ide o konečnú sadu alebo nie.

Riešenie: Po prvé, analýzou expresie, ktorý opisuje množinu S, sa získa, že ide o sadu skutočných hodnoty X, ktoré sú riešeniami rovnice:

(x -3) (x^2 - 9x + 20) = 0 (*)

Riešenie tejto rovnice je x = 3, čo je skutočné číslo, a preto patrí k S. Existuje však viac riešení, ktoré je možné získať hľadaním riešení kvadratickej rovnice:

Môže vám slúžiť: Distribúcia F: Charakteristiky a cvičenia vyriešené

(x^2 - 9x + 20) = 0

Predchádzajúci výraz môže zohľadniť nasledovne:

(x - 4) (x - 5) = 0

Čo nás vedie k ďalším dvom riešeniam pôvodnej (*) rovnice, ktoré sú x = 4 a x = 5. Stručne povedané, rovnica (*) má roztoky 3, 4 a 5.

Sada S výrazne vyjadrená je taká:

S = 3, 4, 5, čo má kardinalitu 3, a preto je konečná sada.

Cvičenie 4

Existujú dve sady a = 1, 5, 7, 9, 11 a b = x ∊ n / x je par ^ x x < 10 .

Výslovne napíšte sadu B a nájdite únia so setou a. Tiež nájdite odpočúvanie týchto dvoch súborov a uzavrieť.

Riešenie: Sada B sa skladá z prírodných čísel tak, že sú rovnomerné a sú tiež nižšie ako hodnota 10, preto je B do značnej miery napísaný takto:

B = 2, 4, 6, 8

Únia set a s sadou B je:

A b = 1, 2, 4, 5, 6, 7, 8, 9, 11

A odpočúvanie set a s set b je napísané takto:

A ⋂ b = = Ø je prázdna sada. 

Je potrebné poznamenať, že Únia a odpočúvanie týchto dvoch konečných súborov vedú k novým súborom, ktoré sú zase tiež konečné.

Odkazy

1. Zdroje, a. (2016). Základná matematika. Úvod do výpočtu. Luk.com.
2. Garo, m. (2014). Matematika: Kvadratické rovnice: Ako vyrieši kvadratickú rovnicu. Marilù garo.
3. Haeussler, e. F., & Paul, r. Siež. (2003). Matematika pre správu a ekonomiku. Pearson Vzdelanie.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematika 1 september. Prah.
5. Vzácny, c. Tón. (2005). Kurz matematiky 3o. Redakčný progreso.
6. Matematika 10 (2018). „Príklady konečných súborov“. Zdroj: Mathematics10.slepo
7. Rock, n. M. (2006). Algebra I je ľahká! Tak ľahké. Tímová rocková tlač.
8. Sullivan, J. (2006). Algebra a trigonometria. Pearson Vzdelanie.
9. Wikipedia. Konečná súprava. Obnovené z: je.Wikipedia.com