Ortonormálne základné vlastnosti, príklady a cvičenia

A Ortonormálna základňa Vytvára sa navzájom kolmými vektormi a ktorých modul má hodnotu 1 (jednotkové vektory). Pamätajte, že základňa B vo vektorovom priestore Vložka, Je definovaný ako súbor lineárne nezávislých vektorov schopných generovať tento priestor.

Vektorový priestor je zase abstraktnou matematickou entitou, medzi ktorej prvky sú vektory, všeobecne spojené s fyzikálnymi veľkosťami, ako je rýchlosť, pevnosť a posun alebo tiež s matkami, polynómami a funkciami.

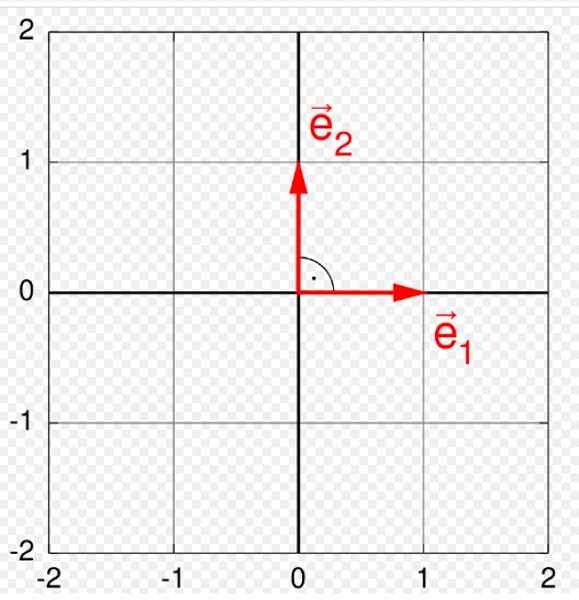
postava 1. Ortonormálna základňa v lietadle. Zdroj: Wikimedia Commons. Quartl [CC By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)].

Vektory majú tri výrazné prvky: veľkosť alebo modul, smer a význam. Ortonormálna základňa je obzvlášť užitočná na reprezentáciu a prácu s nimi, pretože akýkoľvek vektor, ktorý patrí do určitého vektorového priestoru Vložka, Môže byť napísaný ako lineárna kombinácia vektorov, ktoré tvoria ortonormálnu základňu.

Týmto spôsobom sa operácie medzi vektormi, ako je súčet, odčítanie a rôzne typy produktov definovaných v uvedenom priestore.

Medzi najpoužívanejšie základy fyziky patrí základňa tvorená jednotkovými vektormi Jo, J a klimatizovať Predstavujúce tri výrazné smery trojrozmerného priestoru: vysoký, široký a hĺbka. Tieto vektory sú známe aj pod názvom Jednotné kanonické vektory.

Keby sa namiesto toho vektory pracovali na lietadle, stačilo by to s dvoma z týchto troch komponentov, zatiaľ čo iba jedna.

[TOC]

Základne

1- základňa B Je to najmenšia možná sada vektorov, ktoré generujú vektorový priestor Vložka.

2- prvky B Sú lineárne nezávislé.

3- Akákoľvek základňa B vektorového priestoru Vložka, umožňuje vyjadriť všetky vektory Vložka ako jeho lineárna kombinácia a táto forma je jedinečná pre každý vektor. Preto a B Je tiež známy ako Generátorový systém.

4- Rovnaký vektorový priestor Vložka Môže mať rôzne základne.

Môže vám slúžiť: odstredivka: vzorce, ako sa vypočítajú, príklady, cvičenia

Príklady základní

Pod niekoľkými príkladmi ortonormálnych báz a základní všeobecne:

Kanonická základňa v ℜ ⁿ

Tiež nazývaná prírodná základňa alebo štandardná základňa ℜ ⁿ, Kde ℜ ⁿ Je to priestor n-dimenzionálny, Napríklad tri rozmerové miesto je ℜ ³. Na hodnotu n To sa nazýva rozmer vektorového priestoru a označuje ako Dim (v).

Všetky vektory, ktoré patria do ℜ ⁿ Sú zastúpené N-usa Usporiadaný. Pre priestor ℜⁿ, Kanonická základňa je:

a₁ =; a₂ =; a_n =

V tomto príklade sme použili zápis s zátvorkami alebo „držiakmi“ a tučnými vektormi jednotkových vektorov a₁, a₂, a₃..

Kanonická základňa v ℜ³

Rodinné vektory Jo, J a klimatizovať Priznávajú to isté zastúpenie a stačí na to, aby tri reprezentovali vektory v ℜ ³:

Jo =; J =;  klimatizovať =

To znamená, že základ je možné vyjadriť takto:

B = ; ;

Na overenie, či sú lineárne nezávislé, determinant, ktorý s nimi vytvoril vektory, nie sú nenáročné a tiež sa rovná 1:

Musí byť tiež možné napísať ľubovoľného vektora, ktorý patrí do ℜ ³ Ako lineárna kombinácia z nich. Napríklad sila, ktorej obdĺžnikové komponenty sú f_X = 4 n, f_a = -7 n a f_z= 0 n by sa napísal vo vektorovej podobe takto:

F = N = 4Jo -7J + 0klimatizovať N.

Preto Jo, J a klimatizovať Make Up ℜ Generátorový systém ³.

Iné ortonormálne základne v ℜ³

Štandardná základňa opísaná v predchádzajúcej časti nie je jedinou ortonormálnou základňou v ℜ³. Tu máme napríklad základy:

B₁ = ; ;

B₂ = ; ;

Dá sa preukázať, že tieto základne sú ortonormálne, pretože si pamätáme podmienky, ktoré musia byť splnené:

Môže vám slúžiť: zvlnená optika

-Vektory, ktoré tvoria základňu, musia byť navzájom ortogonálne.

-Každý z nich musí byť jednotný.

Môžeme to overiť s vedomím, že determinant, ktorý vytvorili, musí byť nenáročný a rovný 1.

Základňa B₁ Presne je to valcové súradnice ρ, φ a z, ďalší spôsob vyjadrovania vektorov vo vesmíre.

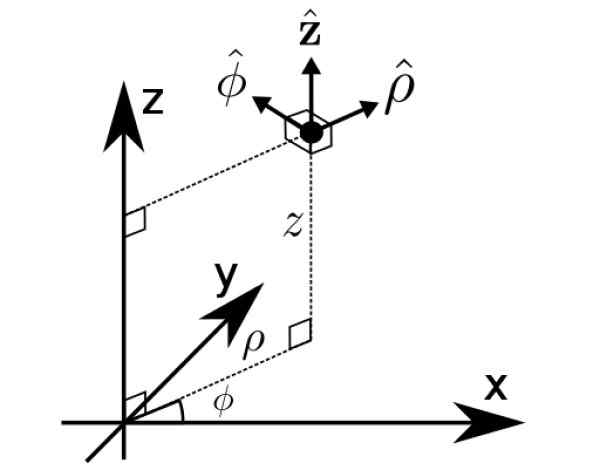Obrázok 2. Valcové súradnice. Zdroj: Wikimedia Commons. Matematický buff [CC By-S (https: // creativeCommons.Org/licencie/By-SA/4.0)].

Vyriešené cvičenia

- Cvičenie 1

Ukážte, že základňa B = ; ; je ortonormálne.

Riešenie

Aby sme ukázali, že vektory sú navzájom kolmé, použijeme skalárny produkt, ktorý sa tiež nazýva interný alebo produktový bod dvoch vektorov.

Nechajte akékoľvek dva vektory alebo a vložka, Váš skalárny produkt je definovaný podľa:

alebo • v = alebo.vložka. cosθ

Na rozlíšenie vektorov od ich modulov použijeme tučný. 9 je uhol medzi alebo a vložka, Preto, ak sú kolmé, znamená to, že 9 = 90 ° a skalárny produkt je neplatný.

Alternatívne, ak sú vektory uvedené z hľadiska ich komponentov: alebo = X, alebo_a,alebo_z > a vložka = X, vložka_a,vložka_z >, skalárny produkt oboch, ktorý je komutatívny, sa počíta týmto spôsobom:

alebo • v = alebo_X .vložka_X + alebo_a .vložka_a + alebo_z .vložka_z

Týmto spôsobom sú skalárne produkty medzi každým párom vektorov:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Pre druhú podmienku sa vypočíta modul každého vektora, ktorý sa získa:

│u │ = √ (u_X² + alebo_a² + alebo_z²)

Moduly každého vektora sú teda:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Môže vám slúžiť: Druhá rovnovážna podmienka: Vysvetlenie, príklady, cvičenia

│ = √ [0² + 0²  + 1²)] = 1

Preto sú tri jednotkové vektory. Nakoniec, determinant, ktorý tvoria, nie je nulová a rovná sa 1:

- Cvičenie 2

Napíšte súradnice vektorov W = Pokiaľ ide o predchádzajúcu základňu.

Riešenie

Na tento účel sa používa nasledujúca veta:

Nech b = vložka₁, vložka₂, vložka₃,.. vložka_n Ortonormálna základňa v priestore V s domácim produktom, vektor W Je reprezentovaný B takto:

W = <W•vložka₁> vložka₁ + <W•vložka₂> vložka₂ +<W•vložka₃> vložka₃ +.. <W•vložka_n> vložka_n

To znamená, že môžeme písať vektor na základni B, prostredníctvom koeficientov <W•vložka₁>, <W•vložka₂>, ..  <W•vložka_n>, pre ktoré musíte vypočítať uvedené skaláre:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

So získanými skalárnymi výrobkami sa vybuduje matica, ktorá sa nazýva koordinovaná matica w.

Preto vektor súradnice W V základni B sú vyjadrené prostredníctvom:

[W]_B= [(18/5); (1/5); 1]

Súradnicová matica nie je vektor, pretože vektor nie je rovnaký ako jej súradnice. Toto je iba súbor čísel, ktoré slúžia na vyjadrenie vektora na danej základni, nie vektor ako taký. Závisia tiež od vybranej základne.

Nakoniec, po vete, vektor W by sa vyjadrilo takto:

W = (18/5) vložka₁ + (1/5) vložka₂ + vložka₃

S: vložka₁ =; vložka₂ =; vložka₃ =, To znamená, základné vektory B.

Odkazy

1. Larson, R. Základy lineárnej algebry. 6. Vydanie. Učenie sa.
2. Larson, R. 2006. Kalkulácia. 7. Vydanie. Zväzok 2. McGraw Hill.
3. Salas, J. lineárna algebra. Téma 10. Ortonormálne základne. Získané z: OCW.Uc3m.je.
4. Univerzita. Valcové súradnice. Vektorová základňa. Získané z: Laplace.my.je.
5. Wikipedia. Ortonormálna základňa. Obnovené z: je.Wikipedia.orgán.