Typy pravdepodobnosti axiómov, vysvetlenie, príklady, cvičenia

Ten axiómy pravdepodobnosť Sú to matematické návrhy týkajúce sa teórie pravdepodobnosti, ktoré si zaslúžia demonštráciu. Axiómy založili v roku 1933 ruský matematik Andrei Kolmogorov (1903-1987) vo svojej práci Základy teórie pravdepodobnosti a položil základ matematického štúdia pravdepodobnosti.

Pri vykonávaní určitého náhodného experimentu ξ je priestor vzorky so všetkými možnými výsledkami experimentu, ktorý sa tiež nazýva diania. Akákoľvek udalosť je označená ako a a p (a) je pravdepodobnosť, že sa bude diať. Potom Kolmogorov zistil, že:

postava 1. Pravdepodobnosť axiómy umožňujú vypočítať pravdepodobnosť zasiahnutia hazardných hier ako ruleta. Zdroj: Pixabay.

-Axióm 1 (bez negativity): Pravdepodobnosť, že dôjde k každej udalosti, je vždy kladná alebo nula, P (a) ≥0. Ak je pravdepodobnosť udalosti 0, nazýva sa to Nemožná udalosť.

-Axióm 2 (istota): za predpokladu, že nejaká udalosť, ktorá patrí do E, jej pravdepodobnosť výskytu je 1, ktorú môžeme vyjadriť ako P (e) = 1. Je to, čo je známe ako a Bezpečný, Pretože pri vykonávaní experimentu je výsledok so všetkou istotou.

-Axióm 3 (pridanie): V prípade dvoch alebo viacerých nekompatibilných udalostí dve až dva, povolané₁, Do₂, Do₃..., pravdepodobnosť udalosti₁ viac a₂ viac a₃ A tak ďalej, je to súčet pravdepodobností, že každá z nich sa stáva osobitne.

Toto je vyjadrené ako: P (a₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Obrázok 2. Pozoruhodný ruský matematik Andrei Kolmogorov (1903-1987), ktorý položil základy pre axiomatickú pravdepodobnosť. Zdroj: Wikimedia Commons.

[TOC]

Príklad

Pravdepodobné axiómy sa široko používajú v mnohých aplikáciách. Napríklad:

Do vzduchu sa hodí pazúr alebo tachuela, a keď padá podlaha, existuje možnosť pádu s špičkou hore (u) alebo s špičkou nadol (d) (nebudeme brať do úvahy iné možnosti). Vzorový priestor tohto experimentu pozostáva z týchto udalostí, potom e = u, d.

Môže vám slúžiť: Revolučné pevné látky: objem, typy, vyriešené cvičeniaObrázok 3. V experimente pri spustení tachuely existujú dve udalosti rôznych pravdepodobností: spadnúť s špičkou nahor alebo na podlahu. Zdroj: Pixabay.

Aplikáciou axiómov, ktoré máme:

P (e) = 1 (Axióm 2)

ale P (e) = p (u) + p (d) (Axióm 3), pretože tieto udalosti sú vzájomne nekompatibilné alebo nesúvisí. Chyba nespadá s špičkou nahor alebo nadol súčasne, je to jeden alebo druhý, ale nie oboje, pretože sa uvažujú o iných možnostiach. Tak:

P (u) + p (d) = 1

P (u) = 1 - p (d)

Ak je rovnako pravdepodobné, že spadne s špičkou nahor alebo nadol, P (u) = p (d) = ½ (Axióm 1). Môže sa však stať, že v dôsledku konštrukcie a dizajnu chyby. Napríklad to môže byť P (u) = ¾ zatiaľ čo P (d) = ¼ (Axióm 1).

Všimnite si, že v obidvoch prípadoch je súčet pravdepodobností 1. Axiómy však nenaznačujú, ako prideliť pravdepodobnosti, aspoň nie úplne. Ale potvrdzujú, že ide o čísla medzi 0 a 1 a že, ako sa v tomto prípade vyskytuje súčet všetkých 1.

Spôsoby, ako priradiť pravdepodobnosť

Pravdepodobnosť axiómy nepredstavujú metódu priradenia hodnoty pravdepodobnosti. Z tohto dôvodu existujú tri možnosti, ktoré sú kompatibilné s axiómmi:

Laplace

Každej udalosti je priradená rovnaká pravdepodobnosť, že sa bude diať, potom je pravdepodobnosť výskytu definovaná ako:

P (a) = počet prípadov priaznivých pre udalosť a/ počet možných prípadov

Napríklad, aká je pravdepodobnosť extrahovania esa z paluby francúzskych kariet? Paluba má 52 kariet, 13 z každej palice a sú tu 4 tyčinky. Každá palica má 1 ako, takže celkovo existujú 4 es:

P (as) = ​​4/52 = 1/13

Laplaceho pravidlo je obmedzené na konečné vzorové priestory, kde každá udalosť je rovnako pravdepodobná.

Môže vám slúžiť: diskrétna matematika

Relatívna frekvencia

Tu musí byť experiment opakovateľný, pretože táto metóda je založená na vykonaní veľkého počtu opakovaní.

Urobme opakovania experimentu ξ, z ktorého zistíme, že n je počet, koľkokrát sa vyskytuje určitá udalosť A, potom pravdepodobnosť, že sa táto udalosť stane, je:

P (a) = lim_{I → ∞} (Ani)

Kde n/i je relatívna frekvencia udalosti.

Definujte p (a) týmto spôsobom spĺňa Kolmogorovove axiómy, ale má nepríjemnosti, že sa musí vykonať mnoho testov, aby bola pravdepodobná pravdepodobnosť vhodná.

Subjektívna metóda

Osoba alebo skupina ľudí sa môže dohodnúť na pridelení pravdepodobnosti udalosti prostredníctvom svojich vlastných rozsudkov. Táto metóda má nevýhodu, že rôzni ľudia môžu k tej istej udalosti priradiť rôzne pravdepodobnosti.

Cvičenie

V experimente súčasného spustenia 3 čestných mien získate šance na opísané udalosti:

a) 2 tváre a kríž.

b) 1 tvár a dva kríže

c) 3 kríženia.

d) aspoň 1 tvár.

Roztok

Tváre sú označené C a krížmi s x. Existuje však niekoľko spôsobov, ako získať dve tváre a kríž. Napríklad prvé dve mince môžu spadnúť s tvárou a tretí s Cruz. Alebo prvá môže spadnúť tvár, druhý kríž a tretí tvár. A nakoniec prvý môže byť kríž a zostávajúce tváre.

Na zodpovedanie otázok je potrebné poznať všetky možnosti, ktoré sú opísané v nástroji s názvom stromový diagram ani Strom pravdepodobnosti:

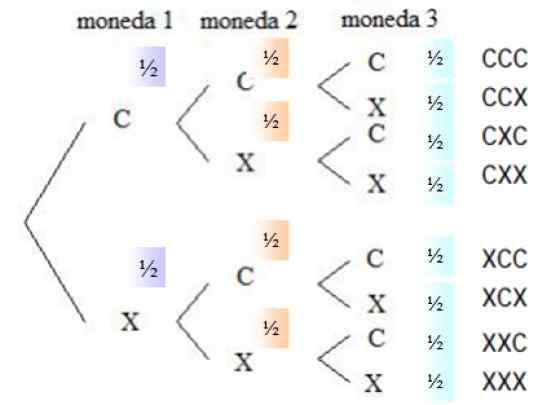Obrázok 4. Schéma stromov na súčasné spustenie troch čestných mincí. Zdroj: f. Zapata.

Pravdepodobnosť, že v akejkoľvek mene je drahá, je ½, to isté sa deje pre kríže, pretože mena je čestná. V pravom stĺpci sú uvedené všetky možnosti spustenia, to znamená vzorový priestor.

Môže vám slúžiť: štatistické premenné

Kombinácie, ktoré reagujú na požadovanú udalosť, sú vybrané zo vzorového priestoru, pretože poradie, v ktorom sa objavia tváre, nie je dôležité. Existujú tri priaznivé udalosti: CCX, CXC a XCC. Pravdepodobnosť každej udalosti je:

P (ccx) = ½. ½ . ½ = 1/8

To isté sa stane pre udalosti CXC a XCC, každý z nich má 1/8 pravdepodobnosť, že sa stane. Pravdepodobnosť získania presne 2 tvárí je preto súčet pravdepodobností všetkých priaznivých udalostí:

P (2 tváre) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Riešenie B

Nájdenie pravdepodobnosti, že existujú presne dva kríže, je analogický problém s predchádzajúcim, existujú aj tri priaznivé udalosti z priestoru vzorky: CXX, XCX a XXC. Preto:

P (2 kríže) = 3/8 = 0.375

Riešenie c

Intuitívne viem, že pravdepodobnosť získania 3 krížov (alebo 3 tvárí) je nižšia. V tomto prípade je požadovaná udalosť XXX na konci pravého stĺpca, ktorého pravdepodobnosť je:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Riešenie d

Žiada sa, aby získala najmenej 1 tvár, to znamená, že 3 tváre, 2 tváre alebo 1 tvár môžu odísť. Jedinou udalosťou nezlučiteľnou s tým je udalosť, v ktorej vyjdú 3 kríženia, ktorých pravdepodobnosť je 0.125. Preto sa požaduje pravdepodobnosť:

P (aspoň 1 tvár) = 1 - 0.125 = 0.875.

Odkazy

1. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Lipschutz, s. 1991. Séria Schaum: Pravdepodobnosť. McGraw Hill.
4. Obregón, i. 1989.Teória pravdepodobnosti. Redakčná limusa.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.