Údaje nie sú zoskupené príklady a cvičenie vyriešené

Ten NEPRUDNÉ ÚDAJE Sú to tie, ktoré získané zo štúdie ešte nie sú organizované podľa tried. Ak ide o zvládnuteľný počet údajov, zvyčajne 20 alebo menej, a existuje niekoľko rôznych údajov, možno s nimi považovať za zoskupené a extrahovať z nich cenné informácie.

Údaje, ktoré nie sú v skupine, pochádzajú z prieskumu alebo štúdie vykonanej na ich získanie, a preto chýba spracovanie. Pozrime sa na niekoľko príkladov:

postava 1. Nepregroupované údaje pochádzajú priamo z akejkoľvek štúdie a neboli klasifikované. Zdroj: pxhere.

-Výsledky skúšky CI intelektuálneho koeficientu na 20 náhodných študentoch z univerzity. Získané údaje boli nasledujúce:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112,106

-Vek 20 zamestnancov veľmi populárnej kaviarne:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 22, 23, 23, 19, 22, 27, 29, 23, 20

-Priemerné záverečné poznámky 10 študentov triedy matematiky:

3.2; 3.1; 2,4; 4,0; 3,5; 3,0; 3,5; 3,8; 4.2; 4.9

[TOC]

Vlastnosti údajov

Existujú tri dôležité vlastnosti, ktoré charakterizujú súbor štatistických údajov zoskupené alebo nie, ktoré sú:

-Pozícia, čo je tendencia údajov zoskupovať okolo určitých hodnôt.

-Rozptyl, Svedectvo o tom, ako sú rozptýlené alebo šírené, sú údaje okolo určitej hodnoty.

-Forma, Vzťahuje sa na spôsob, akým sú údaje distribuované, čo je možné vidieť, keď je zostavený ich graf. Existujú veľmi symetrické a tiež skreslené krivky, buď vľavo, alebo napravo od určitej centrálnej hodnoty.

Pre každú z týchto vlastností existuje niekoľko opatrení, ktoré ich opisujú. Po získaní nám poskytnú panorámu správania údajov:

-Najpoužívanejšími polohovými opatreniami sú aritmetické priemerné alebo jednoducho stredné, stredné a módy.

-Pri disperzii sa často používa rozptyl a štandardná odchýlka, ale nie sú jedinými disperznými opatreniami.

Môže vám slúžiť: homotecia

-A na určenie formulára sa priemer a medián porovnávajú prostredníctvom zaujatosti, ako bude vidieť čoskoro.

Výpočet priemerných, stredných a módnych

-Aritmetický priemer, Známy tiež ako priemerný a označený ako X, počíta sa takto:

X = (x₁ + X₂ + X₃ +... X_n) / n

Kde x₁, X₂,.. . X_n, sú údaje a n sú ich súčtom. Stručne povedané, suma je:

Index I predstavuje údaje 1, údaje 2, údaje 3 atď., Až do jediného, ​​čo je posledný.

-Stredný Je to hodnota, ktorá sa objaví v strede usporiadaného sukcesie údajov, takže na ich získanie je potrebné najskôr objednať údaje.

Ak je počet pozorovaní čudný, nie je problém nájsť strednú hodnotu, ale ak máme pár údajov, tieto dve centrálne údaje sa vyhľadávajú a spriemerujú.

-Formovať Je to najbežnejšia hodnota pozorovaná v súbore údajov. Neexistuje vždy, pretože je možné, že žiadna hodnota sa opakuje častejšie ako iná. Môže existovať aj dva údaje s rovnakou frekvenciou, v takom prípade sa hovorí o dvojmodálnej distribúcii.

Na rozdiel od predchádzajúcich dvoch opatrení je možné módu použiť s kvalitatívnymi údajmi.

Pozrime sa, ako sa tieto opatrenia polohy počítajú s príkladom:

Vyriešený príklad

Predpokladajme, že chcete určiť aritmetický priemer, medián a módu v príklade navrhnutom na začiatku: vek 20 zamestnancov kaviarne:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 22, 23, 23, 19, 22, 27, 29, 23, 20

Ten polovica Vypočíta sa jednoducho pridaním všetkých hodnôt a vydelením n = 20, čo je celkový počet údajov. Tadiaľto:

Môže vám slúžiť: Vzťahy proporcionality: koncept, príklady a cvičenia

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 roky.

Nájsť stredný Najskôr je potrebné objednať súbor údajov:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Rovnako ako niekoľko údajov, dva centrálne údaje, zvýraznené tučným písmom, sú odobraté a spriemerované. Pretože obidve sú 22, medián je 22 rokov.

Nakoniec formovať Je to skutočnosť, že sa najviac opakuje alebo že je frekvencia väčšia, je to 22 rokov.

Rozsah, rozptyl, štandardná odchýlka a zaujatosť

Rozsah je jednoducho rozdiel medzi hlavnými a najmenšími údajmi a umožňuje ich variabilitu rýchlo oceniť. Ale okrem toho existujú aj ďalšie disperzné opatrenia, ktoré ponúkajú viac informácií o distribúcii údajov.

Rozptyl a štandardná odchýlka

Rozptyl je označený ako S a vypočíta sa výrazom:

Často sa pracuje s kvázianciou namiesto rozptylu, ktorý sa vypočíta rovnakým spôsobom, iba vydelený N-1, namiesto toho, aby robil n:

Pretože rozptyl je súčet štvorcov, vedie k štvorcovi vzorovej jednotky. Napríklad pri štúdiu veku zamestnancov v kaviarni by rozptyl prišiel v rokoch².

Potom je definovaná štandardná odchýlka, ako je druhá odmocnina, alebo tiež štandardná kvázi devivácia, ktorá je odmocninou kvázivariancie:

Zaujatosť

Je to porovnanie priemerného X a strednej mediálu:

-Áno Med = médiá x: Údaje sú symetrické.

-Keď x> med: zaujatý napravo.

-A ak x < Med: los datos sesgan hacia la izquierda.

Cvičenie

Nájdite priemer, medián, módu, hodnosť, rozptyl, štandardnú odchýlku a zaujatosť pre výsledky intelektuálnej koeficientnej skúšky 20 študentov z univerzity:

Môže vám slúžiť: matematické funkcie

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Riešenie

Objednávame údaje, pretože bude potrebné nájsť medián.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

A uvedieme ich do tabuľky nasledovne, aby sme uľahčili výpočty. Druhý stĺpec s názvom „Akumulovaný“ je súčet zodpovedajúcich údajov plus predchádzajúci.

Tento stĺpec ľahko nájde priemer, ktorý rozdelí poslednú akumulovanú medzi celkový počet údajov, ako je vidieť na konci „akumulovaného“ stĺpca:

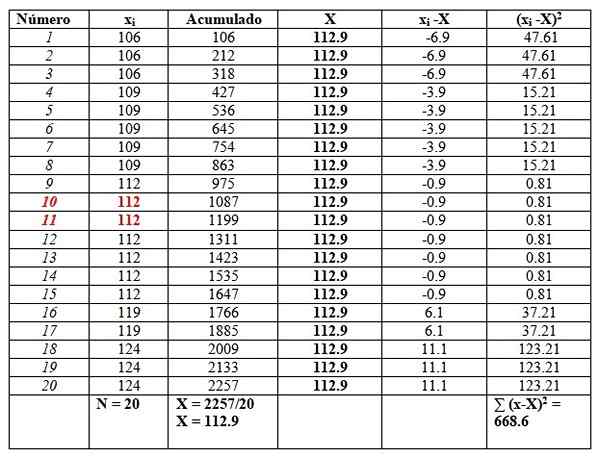
X = 112.9

Medián je priemer centrálnych údajov zvýraznených červenou farbou: číslo 10 a číslo 11. Rovnako ako to isté, medián je 112.

Nakoniec, móda je hodnota, ktorá sa najviac opakuje a je 112, so 7 opakovaniami.

Pokiaľ ide o disperzné opatrenia, rozsah je:

124-106 = 18.

Rozptyl sa získa vydelením konečného výsledku pravého stĺpca medzi n:

S = 668.6/20 = 33.42

V tomto prípade je štandardná odchýlka odmocninou rozptylu: √33.42 = 5.8.

Na druhej strane, hodnoty kvázivátnosti a kvázi štandardná odchýlka sú:

siež_c= 668.6/19 = 35.2

Štandardná kvázi devivácia = √35.2 = 5.9

Nakoniec je zaujatosť mierne doprava, od priemeru 112.9 je väčší ako stredný 112.

Odkazy

1. Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
2. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
3. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
4. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.