Definícia curtózy, typy, vzorce, na čo je napríklad

Ten Curtóza Je to štatistický parameter, ktorý slúži na charakterizáciu rozdelenia pravdepodobnosti náhodnej premennej, čo naznačuje stupeň koncentrácie hodnôt okolo centrálneho opatrenia. Toto je tiež známe ako „špičková známka“.

Termín pochádza z gréckeho „Kurtos“, čo znamená klenuté, preto curtóza naznačuje stupeň smerovania alebo sploštenia distribúcie, ako je vidieť na nasledujúcom obrázku:

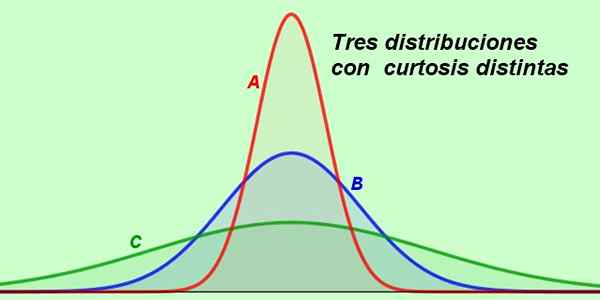
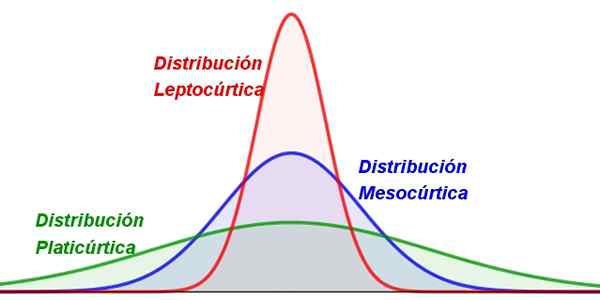postava 1. Rôzne typy curtózy. Zdroj: f. Zapata.

Takmer všetky hodnoty náhodnej premennej majú tendenciu zoskupovať sa okolo centrálnej hodnoty, ako je priemer. Ale v niektorých distribúciách sú hodnoty rozptýlené viac ako u iných, čo vedie k sploštenejším alebo viac štíhlym krivkám.

[TOC]

Definícia

Curtóza je numerická hodnota každej frekvenčnej distribúcie, ktorá je podľa koncentrácie hodnôt okolo priemeru klasifikovaná do troch skupín:

-Leptokurické: v ktorých sú hodnoty veľmi zoskupené okolo priemeru, takže distribúcia je celkom špicatá a štíhla (obrázok 1, vľavo).

-Mezocuric: Má miernu koncentráciu hodnôt okolo priemeru (obrázok 1 v strede).

-Phylicuric: Táto distribúcia má širší tvar, pretože hodnoty majú tendenciu byť rozptýlené (obrázok 1 vpravo).

Vzorce a rovnice

Curtóza môže mať akúkoľvek hodnotu, bez obmedzení. Jeho výpočet sa vykonáva v závislosti od spôsobu, akým sa údaje poskytujú. Zápis použitý v každom prípade je nasledujúci:

-Koeficient kortózy: g₂

-Aritmetický priemer: X alebo x s barom

-I-eme: X_Jo

-Štandardná odchýlka: σ

-Počet údajov: N

-Frekvencia I-esimu: F_Jo

-Značka triedy: mX_Jo

S týmto zápisom uvádzame niektoré z najbežnejšie používaných vzorcov na nájdenie curtózy:

Môže vám slúžiť: Vektorový priestor: základňa a rozmer, axiómy, vlastnosti

- Curtóza podľa prezentácie údajov

Bez zoskupenia alebo zoskupených údajov pri frekvenciách

Údaje zoskupené v intervaloch

Nadbytok curtózy

Tiež nazývaný Fisherov koeficient ani Rybárska miera, Slúži na porovnanie študovanej distribúcie s normálnym rozdelením.

Keď má prebytočná curtóza hodnota 0, sme v prítomnosti normálneho rozdelenia alebo Gauss Bell. Týmto spôsobom, pokiaľ sa vypočíta nadmerné opaľovanie distribúcie, v skutočnosti ho porovnávame s normálnym rozdelením.

Pre údaje bez zoskupenia, ako aj pre zoskupené údaje, koeficient Fisher Pointing Coeficient, označený K, je:

K = g₂ - 3

Dá sa však preukázať, že curtóza normálneho rozdelenia je 3, preto, ak je koeficient smerovania Fisherov 0 alebo blízko 0 a existuje mezokurické rozdelenie. Ak k> 0 je distribúcia leptokurická a ak k<0 es platicúrtica.

Čo je curtóza pre?

Curtóza je miera variability použitej na charakterizáciu morfológie distribúcie. Týmto spôsobom je možné symetrické distribúcie porovnávať s rovnakým priemerom a rovnakým disperziou (uvedeným štandardnou odchýlkou).

Opatrenia s variabilitou zaisťujú, že priemery sú spoľahlivé a pomáha riadiť variácie distribúcie. Napríklad, analyzme tieto dve situácie.

3 oddelenia platy

Predpokladajme, že nasledujúci graf ukazuje distribúcie v plate 3 oddelení tej istej spoločnosti:

Obrázok 2. Tri rôzne distribúcie ilustrujú praktické situácie. (Pripravil Fanny Zapata)

Krivka A je najškrnavejšia zo všetkých a vo svojej podobe sa odvodzuje, že väčšina platov tohto oddelenia je veľmi blízko priemeru, preto väčšina zamestnancov dostáva podobnú kompenzáciu.

Môže vám slúžiť: celé čísla

Pokiaľ ide o svoju časť oddelenia B, platová krivka sleduje normálne rozdelenie, pretože krivka je mezokurická, v ktorej predpokladáme, že platy boli náhodne rozložené.

A nakoniec máme krivku C, ktorá je veľmi sploštená, čo je znamenie, že v tomto oddelení je platový rozsah oveľa širší ako v ostatných.

Výsledky skúšky

Predpokladajme, že teraz tri krivky na obrázku 2 predstavujú výsledky skúšky aplikovanej na tri skupiny študentov toho istého predmetu.

Skupina, ktorej kvalifikácie sú reprezentované krivkou pre leptokuric, je dosť homogénna, najviac získala priemerné alebo blízke hodnotenie.

Je tiež možné, že výsledok bol spôsobený skutočnosťou, že otázky týkajúce sa skúšky mali viac -menej rovnaký stupeň obtiažnosti.

Na druhej strane výsledky skupiny C naznačujú väčšiu heterogenitu v skupine, ktorá pravdepodobne obsahuje priemerných študentov, niektorých vynikajúcich študentov a určite ďalší menej pozorný.

Alebo to môže znamenať, že otázky testu mali veľmi odlišné stupne obtiažnosti.

Krivka B je mezokurická, čo naznačuje, že výsledky testu nasledovali po normálnom rozdelení. Toto je zvyčajne najčastejší prípad.

Vyriešený príklad curtózy

Nájdite Fisherov koeficient ukazovania nasledujúcich stupňov, získaných pri skúške fyziky skupine študentov s mierkou od 1 do 10:

5, 5, 4, 7, 7,7, 9, 8, 9, 4, 3

Riešenie

Nasledujúci výraz sa použije pre údaje, ktoré nie sú skupinové, uvedené v predchádzajúcich oddieloch:

S koeficientom Fishera bodu daný:

Môže vám slúžiť: Pythagorovské identity: demonštrácia, príklad, cvičenia

K = g₂ - 3

Táto hodnota umožňuje poznať typ distribúcie.

Na výpočet g₂ Je vhodné to urobiť usporiadaným spôsobom, krok za krokom, pretože niekoľko aritmetických operácií sa musí vyriešiť.

Krok 1

Po prvé, vypočíta sa priemer kvalifikácie. Existujú n = 11 údajov.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

Krok 2

Nachádza sa štandardná odchýlka, pre ktorú sa používa táto rovnica:

 Použitím kalkulačky so štatistickými funkciami je výsledok okamžitý:

σ = 1.992

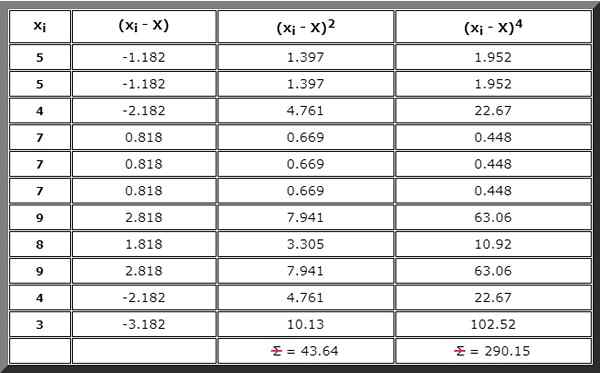
Alebo môžete tiež zostaviť tabuľku, ktorá sa vyžaduje aj pre ďalší krok a v ktorom je napísaný každý termín zhrnutí, počnúc (x_Jo - X), potom (x_Jo - X)² A potom (x_Jo - X)⁴ :

Krok 3

Vykonajte súčet uvedený vo vzorci čitateľa pre g₂. Na tento účel sa používa výsledok pravého stĺpca predchádzajúcej tabuľky:

∑ (X_Jo - X)⁴= 290.pätnásť

Preto:

g₂ = (1/11) x 290.15/1.992⁴ = 1.675

Fisherov značkový koeficient je:

K = g₂ - 3 = 1.675 - 3 = -1.325

Čo je záujmom, je príznak výsledku, ktorý, keď je negatívny, zodpovedá fierom rôznych úrovniach obtiažnosti.

Použitie tabuľky, ako je Excel, výrazne uľahčuje rozlíšenie týchto typov problémov a ponúka tiež možnosť grafu distribúcie.

Odkazy

1. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
2. Marco, f. Obruba. Získané z: ekonómia.com.
3. Oliva, J. Asymetria a curtóza. Zdroj: ŠtatistikauUCV.Súbory.Slovník.com.
4. Spurr, w. 1982. Rozhodovanie v správe. Limusa.
5. Wikipedia. Kurtóza. Zdroj: In.Wikipedia.orgán.