Priemerné vzorce rýchlosti, ako sa vypočíta a vyrieši

Ten priemerná rýchlosť Pre mobilnú častice je definovaná ako dôvod medzi zmenou pozície, ktorú zažíva, a časovým intervalom použitým pri zmene. Najjednoduchšia situácia je situácia, v ktorej sa častica pohybuje pozdĺž priamky predstavovanej osou x.

Predpokladajme, že mobilný objekt zaberá pozície X₁ a x₂ V časoch t₁ a t₂ respektíve. Definícia priemernej rýchlosti vložka_m Je matematicky reprezentovaný takto:

Jednotky vložka_m V medzinárodnom systéme sú merače/sekundy (m/s). Ďalšie bežné jednotky používania, ktoré sa objavujú v mobilných textoch a zariadeniach, sú: KM/H, CM/S, míle/h, nohy/s a ďalšie, za predpokladu, že sú formou dĺžky/času.

Grécke písmeno „δ“ znie „delta“ a používa sa na zhrnutie rozdielu medzi dvoma množstvami.

[TOC]

Charakteristiky priemernej rýchlosti vektora V_m

Priemerná rýchlosť je dôležitou charakteristikou pohybu. Zdroj: Pixabay

Priemerná rýchlosť je vektor, pretože súvisí so zmenou polohy, ktorá je zase známa ako Vektorový posun.

Táto kvalita je zastúpená tučným písmom alebo šípkou cez písmeno, ktoré označuje veľkosť. Avšak v dimenzii je jediným možným smerom smerom x osi, a preto sa dá vydať do zápisu vektora.

Pretože vektory majú veľkosť, smer a význam, počiatočný pohľad na rovnicu naznačuje, že priemerná rýchlosť bude mať rovnaký smer a zmysel ako posun.

Predstavte si častice príkladu, ktorý sa pohybuje po priamke. Na opis vášho pohybu je potrebné uviesť referenčný bod, ktorý bude „pôvodom“ a bude označený ako alebo.

Častica sa môže pohybovať preč alebo blížiaci sa alebo buď doľava alebo doprava. Môžete tiež využiť veľa alebo málo času na dosiahnutie určitej pozície.

Môže vám slúžiť: teplo: vzorce a jednotky, charakteristiky, ako sa meria, príklady

Veľkosti, ktoré boli uvedené: poloha, posun, interval času a priemerná rýchlosť, opisujú správanie sa častice pri pohybe. Je to o veľkosti Kinematický.

Na rozlíšenie pozícií alebo umiestnení vľavo alebo sa použije značka (-) a tie, ktoré sa nachádzajú vpravo alebo prenášajú znamenie (+).

Priemerná rýchlosť má geometrickú interpretáciu, ktorú je možné vidieť na nasledujúcom obrázku. Je to sklon čiary, ktorý prechádza bodmi P a Q. Pri rezaní polohy vs polohu. čas v dvoch bodoch, je to čiara sušenie.

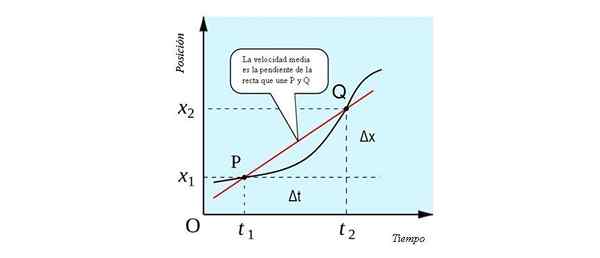Geometrická interpretácia priemernej rýchlosti, ako sklon línie, ktorá sa spája s bodmi P a Q. Zdroj: すじにく シチュー [CC0].

Príznaky priemernej rýchlosti

Pri nasledujúcej analýze sa musí zohľadniť tón₂ > t₁. To znamená, že nasledujúci okamih je vždy väčší ako prúd. Tadiaľto tón₂ - tón₁ Je to vždy pozitívne, čo zvyčajne dáva zmysel denne.

Potom znak priemernej rýchlosti bude určený X₂ - X₁. Všimnite si, že je to dôležité.

Alebo „dopredu“ alebo „späť“, ako čitateľ uprednostňuje.

Ak je priemerná rýchlosť pozitívna, znamená to, že to znamená v priemere hodnota “X”Sa časom zvyšuje, aj keď to neznamená, že by sa mohlo v určitom okamihu uvažovaného času znížiť - Δt -.

Z globálneho hľadiska však na konci času Δt, Skončila s väčšou pozíciou ako tá, ktorú mala na začiatku. Podrobnosti o pohybe sa v tejto analýze ignorujú.

Môžete vám slúžiť: Newtonov tretí zákon: Aplikácie, experimenty a cvičenia

Čo ak je priemerná rýchlosť negatívna? To znamená, že častice končia menšou súradnicou ako tá, s ktorou začala. Režim Groso sa pohyboval dozadu. Pozrime sa na niektoré číselné príklady:

Príklad 1: Vzhľadom na uvedené počiatočné a konečné pozície uveďte znak priemernej rýchlosti. Kam sa častice pohybovali globálne?

a) x₁ = 3 m; X₂ = 8 m

Odpoveď: X₂- X₁  = 8 m - 3 m = 5 m. Pozitívna priemerná rýchlosť, častice sa posunuli vpred.

b) x₁ = 2 m; X₂ = -3 m

Odpoveď: X₂ - X₁ = -3 m -2 m = -5 m. Priemerná negatívna rýchlosť, častice sa posunuli dozadu.

 c) x₁  = - 5 m; X₂ = -12 m

Odpoveď: X₂ - X₁   = -12 m -( -5 m) = -7 m. Priemerná negatívna rýchlosť, častice sa posunuli dozadu.

d) x₁  = - 4 m; X₂ = 10 m

Odpoveď: X₂ - X₁  = 10 m - (-4 m) = 14 m. Pozitívna priemerná rýchlosť, častice sa posunuli vpred.

Môže byť priemerná rýchlosť 0? Jo. Pokiaľ sú východiskový bod a bod príchodu rovnaké. Znamená to, že častice boli nevyhnutne v pokoji stále?

Nie, znamená to iba to, že výlet bol spiatočným výletom. Možno cestoval rýchlo alebo možno veľmi pomaly. Zatiaľ to nie je známe.

Priemerná rýchlosť: skalárna veľkosť

To nás vedie k definovaniu nového termínu: Priemerná rýchlosť. Vo fyzike je dôležité rozlišovať medzi vektorovými veľkosťami a veľkosťami, ktoré nie sú: skalár.

Pre časticu, ktorá sa uskutočnila spiatočnou cestou, je priemerná rýchlosť 0, ale mohla byť veľmi rýchla alebo možno nie. Aby som to vedel, priemerná rýchlosť je definovaná ako:

Jednotky priemernej rýchlosti sú rovnaké ako jednotky priemernej rýchlosti. Základný rozdiel medzi oboma veľkami.

Môže vám slúžiť: fermionický kondenzát: vlastnosti, aplikácie a príklady

Na druhej strane priemerná rýchlosť poskytuje iba číselné informácie. S ňou je známe, ako rýchlo alebo pomaly sa častice pohybujú, ale nie, ak to urobil dopredu alebo dozadu. Preto je to skalárna veľkosť. Ako ich rozlíšiť, aby ich označili? Jedným zo spôsobov je zanechanie odvážnych vektorov alebo na ne vložte šípku.

A je dôležité si uvedomiť, že priemerná rýchlosť sa nemusí rovnať priemernej rýchlosti. Pre spiatočnú cestu je priemerná rýchlosť nula, ale priemerná rýchlosť nie. Obaja majú rovnakú číselnú hodnotu, keď vždy cestujú rovnakým smerom.

Cvičenie

Vraciate sa späť zo školy potichu o 95 km/h na 130 km. Začnite pršať a znižuje rýchlosť na 65 km/h. Po jazde 3 hodiny a 20 minút sa konečne vráti domov.

a) Ako ďaleko je vaša škola domov?

b) Aká bola priemerná rýchlosť?

Odpovede:

a) Niektoré predchádzajúce výpočty sú potrebné:

Výlet je rozdelený na dve časti, celková vzdialenosť je:

D = D1+ D₂, S D1 = 130 km

Celkový čas je 3 hodiny a 20 minút = 3 + 1/3 hodiny = 10/3 hodiny = 3.33 h (je potrebné umiestniť rovnaké jednotky na čas, v tomto prípade je to vhodné).

T2 = 3.33 - 1.37 hodín = 1.96 hodín

Výpočet d_2:

d₂ = 65 km/h x 1.96 h = 125. 4 km.

Škola je D1+ D₂ = 255.4 km od domu.

b) Teraz nájdete priemernú rýchlosť:

Odkazy

1. Giancoli, D. Fyzika. Zásady s aplikáciami. Šieste vydanie. Sála. 21-22.
2. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 20-21.
3. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7mamička. Vydanie. Mexiko. Redaktori učenia sa Cengage. 21-23.