Okamžitá definícia rýchlosti, vzorec, výpočet a cvičenia

Ten okamžitá rýchlosť Je definovaný ako okamžitá zmena posunu v priebehu času. Je to koncept, ktorý dodáva štúdiu pohybu veľkú presnosť. A je to pokrok, pokiaľ ide o priemernú rýchlosť, ktorej informácie sú veľmi všeobecné.

Ak chcete získať okamžitú rýchlosť, pozrime sa na čo najmenší časový interval. Diferenciálny počet je perfektný nástroj na matematické vyjadrenie tejto myšlienky.

Okamžitá rýchlosť predstavuje mobilnú rýchlosť v každom bode svojej trasy. Zdroj: Pixabay.

Východiskovým bodom je priemerná rýchlosť:

Teraz urobme prístup k 0 k 0 všetkým, čo môže. Toto je limit a výsledkom bude presne okamžitá rýchlosť:

Tento limit je známy pod menom derivátu. V zápise diferenciálneho počtu máte:

Za predpokladu, že pohyb je obmedzený na priamu čiaru, môže byť vydaný vektorovým zápisom.

[TOC]

Výpočet okamžitej rýchlosti: geometrická interpretácia

Nasledujúci obrázok ukazuje geometrickú interpretáciu konceptu derivátu: je to sklon čiary dotyčný Do krivky x (t) vs. tón V každom bode.

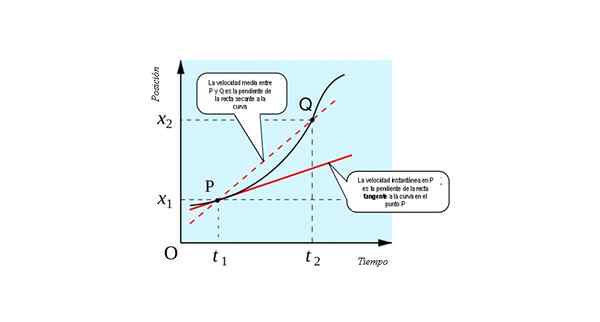Okamžitá rýchlosť v p -ekvivalentnej číselnom s sklonom čiary tangens k krivke x vs. t v bode P. Zdroj: Zdroj: すじにく シチュー [CC0].

Môžete si predstaviť, ako získať limit, ak sa bod Q postupne blíži. Príde čas, keď sú oba body také blízko, že sa nedá odlíšiť od druhého.

Čiara, ktorá ich spája, sa potom suší (rovno, ktorá sa zníži na dva body), aby bola dotyčnica (rovná, ktorá sa dotýka krivky v jednom bode). Preto, aby sme našli okamžitú rýchlosť mobilnej častice, mali by sme mať:

• Graf polohy častice ako funkcia času. Nájdenie sklonu čiary dotýkanej krivky v každom okamihu, máte okamžitú rýchlosť v každom bode, ktorý je obsadená časticou.

Môže vám slúžiť: Ampère Law: Formula a rovnice, demonštrácia, cvičenia

O dobre:

• Funkcia polohy častíc x (t), ktorý je odvodený na získanie funkcie rýchlosti V (t), potom sa táto funkcia vyhodnotí vždy tón, Pohodlie. Funkcia polohy má byť odvoditeľná.

Niektoré špeciálne prípady pri výpočte okamžitej rýchlosti

-Sklon čiary dotyk do krivky v p je 0. Nulová sklon znamená, že mobil je zastavený a že jeho rýchlosť je samozrejme 0.

-Sklon čiary dotyčeného k krivke v p je väčší ako 0. Rýchlosť je pozitívna. Vo vyššie uvedenom grafe to znamená, že mobil sa pohybuje od alebo.

-Sklon čiary dotyčeného k krivke v p je menší ako 0. Rýchlosť by bola negatívna. Vo vyššie uvedenom grafe nie sú také body, ale v takom prípade by sa častica blížila alebo by sa blížila alebo.

-Sklon čiary dotyk do krivky je konštantný v P a všetkých ostatných bodoch. V tomto prípade je graf priamka a mobil má pohyb rovnomernej línie MRU (jej rýchlosť je konštantná).

Všeobecne platí, že funkcia V (t) Je to tiež časová funkcia, ktorá sa môže odvodiť. Čo keby nebolo možné nájsť tie odvodené z funkcií x (t) a V (t)?

V prípade x (t) Je možné, že sklon - okamžitá rýchlosť - výrazne zmenené znaky. Alebo to okamžite prejde z nuly na inú hodnotu.

Ak áno, grafika x (t) Pri náhlych zmenách by to predstavovalo tipy alebo rohy. Veľmi odlišné od prípadu predstavovaného v predchádzajúcom obrázku, v ktorom krivka x (t) Je to mäkká krivka, bez bodov, rohov, diskontinuít alebo náhlych zmien.

Môže vám slúžiť: kondenzát Bose Einstein

Pravda je taká, že pre skutočné mobilné mobilné krivky sú mäkké krivky tie, ktoré najlepšie predstavujú správanie objektu.

Všeobecný pohyb je dosť zložitý. Mobil je možné na chvíľu zastaviť, zrýchliť, aby ste sa presunuli z odpočinku, aby ste mali rýchlosť a utiekli sa z východiskového bodu, na chvíľu udržiavajte rýchlosť, potom sa zastavte znova a teda štýl.

Môžu začať znova a pokračovať rovnakým smerom. Alebo konajte neúspech a vráťte sa. Toto sa nazýva rozmanitý pohyb v dimenzii.

Pod niektorými príkladmi výpočtu okamžitej rýchlosti objasní použitie daných definícií:

Vyriešené cvičenia s okamžitou rýchlosťou

Cvičenie 1

Častica sa pohybuje po priamke s nasledujúcim zákonom o pohybe:

x (t) = -t³ + 2 t² + 6 t - 10

Všetky jednotky sú v medzinárodnom systéme. Nájsť:

a) Poloha častice pri t = 3 sekundy.

b) priemerná rýchlosť v intervale medzi t = 0 s a t = 3 s.

c) priemerná rýchlosť v intervale medzi t = 0 s a t = 3 s.

d) Okamžitá rýchlosť častice predchádzajúcej otázky, t = 1 s.

Odpovedať

a) Na nájdenie polohy častice, zákon o pohybe (funkcia polohy) pri t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Nie je problém, že pozícia je negatívna. Znak (-) naznačuje, že častica je vľavo od pôvodu alebo.

b) Pri výpočte priemernej rýchlosti sú konečné a počiatočné polohy častice potrebné v uvedených časoch: x (3) a x (0). Pozícia pri t = 3 je x (3) a je známa o predchádzajúcom výsledku. Pozícia v t = 0 sekundy je x (0) = -10 m.

Môže vám slúžiť: statická: história, aké štúdie, aplikácie, zákony

Keďže konečná pozícia je rovnaká ako tá pôvodná, okamžite sa dospelo k záveru, že priemerná rýchlosť je 0.

c) Priemerná rýchlosť je dôvodom medzi cestovanou vzdialenosťou a časom stráveným časom. Teraz je vzdialenosť modul alebo veľkosť posunu:

Vzdialenosť = | x2 - x1 | = | -10-(-10) | M = 20 m

Upozorňujeme, že prejdená vzdialenosť je vždy pozitívna.

vložka_{m = 20 m/3 s = 6.7 m/s}

d) Tu je potrebné nájsť prvý derivát pozície týkajúcej sa času. Potom sa vyhodnotí na t = 1 sekundu.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Cvičenie 2

Nižšie je graf polohy mobilu ako funkcia času. Nájdite okamžitú rýchlosť pri t = 2 sekundy.

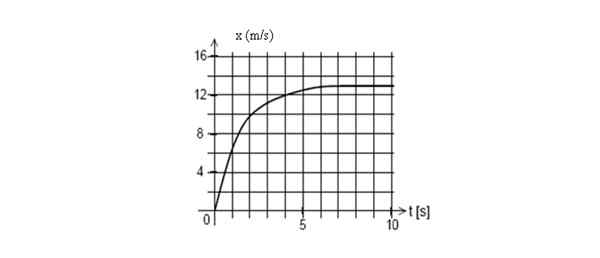Graf polohy verzus čas pre mobil. Zdroj: Self Made.

Odpoveď

Nakreslite dotyčnú čiaru k krivke za t = 2 sekundy, potom vypočítajte svoj sklon a získajte dva body riadku.

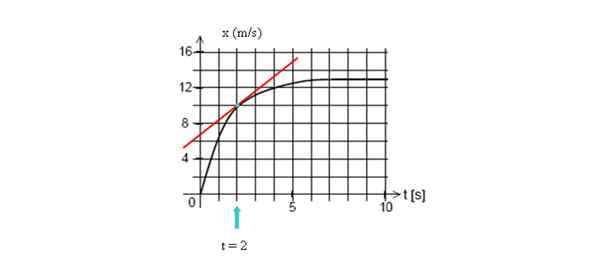Ak chcete vypočítať okamžitú rýchlosť v uvedenom bode, nakreslite dotyčničku do tohto bodu a nájdite jej sklon. Zdroj: Self Made.

V tomto príklade budeme mať dva body, ktoré sa ľahko vizualizujú, ktorých súradnice sú (2 s, 10 m) a rez s vertikálnou osou (0 s, 7 m):

Odkazy

1. Giancoli, D. Fyzika. Zásady s aplikáciami. 6^th Vydanie. Sála. 22-25.
2. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 21-22.
3. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Vydanie. Mexiko. Redaktori učenia sa Cengage. 23-25.