Priemerná definícia a vzorce uhlovej rýchlosti, vyriešené cvičenia

Ten Priemerná uhlová rýchlosť rotácie je definovaná ako uhol otáčaný polohou vektorovej časovej jednotky bodu, ktorý opisuje kruhový pohyb. Čepele stropného ventilátora (ako je ten, ktorý je znázornený na obrázku 1), nasledujú kruhový pohyb a jeho priemerná uhlová rýchlosť rotácie sa vypočítava prevzatím pomeru medzi uhlom zmeny a časom, v ktorom sa tento uhol prešiel.

Pravidlá, ktoré nasledujú hnutie rotácie. Vzdialenosti sa môžu merať aj v metroch, avšak uhlové veľkosti majú osobitný význam, pretože výrazne uľahčujú opis pohybu.

postava 1. Čepele ventilátorov majú uhlovú rýchlosť. Zdroj: Pixabay

Grécke písmená sa zvyčajne používajú pre uhlové veľkosti a latinské písmená pre zodpovedajúce lineárne veľkosti.

[TOC]

Definícia a vzorce

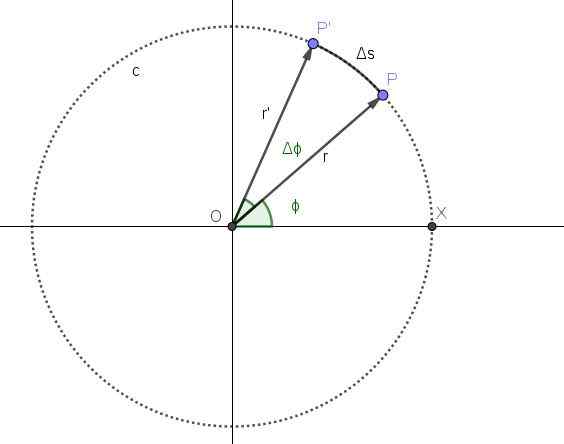
Obrázok 2 predstavuje pohyb bodu na kruhovej trajektórii C. Poloha P bodu zodpovedá okamžitému t a uhlovej polohe zodpovedajúcej tomuto okamihu je ϕ. 

Od okamihu, keď uplynie časové obdobie Δt. V tomto období je nová poloha bodu p 'a uhlová poloha zvýšila uhol Δϕ.

Obrázok 2. Kruhový pohyb bodu. Zdroj: Self Made

Priemerná uhlová rýchlosť Ω je uhol prejdený na jednotku času, takže kvocient δϕ/Δt bude predstavovať priemernú uhlovú rýchlosť medzi momentmi T a T+A:

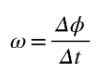
Pretože uhol sa meria v radiánoch a čas za sekundu, jednota priemernej uhlovej rýchlosti je rad/s. Ak chcete vypočítať uhlová rýchlosť Práve v čase t, potom bude kvocient ϕ/Δt vypočítaný, keď Δt ➡0 bude.

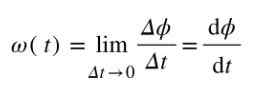Jednotka miery okamžitej uhlovej rýchlosti je tiež rad/s.

Môže vám slúžiť: 31 typov sily vo fyzike a ich charakteristiky

Jednotná rotácia

Pohyb rotácie je rovnomerný, ak je kedykoľvek pozorovaný, uhol je rovnaký v rovnakom časovom období. Ak je rotácia rovnomerná, potom sa uhlová rýchlosť kedykoľvek zhoduje s priemernou uhlovou rýchlosťou.

V rovnomernom rotácii sa čas, v ktorom sa nazýva úplný zákrut obdobie A je označený t t. 

Okrem toho, keď je cestovaný uhol, je 2π, takže v rovnomernej rotácii je uhlová rýchlosť Ω príbuzná s nasledujúcim vzorcom:

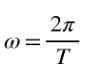
Ten časť F rovnomernej rotácie, ako je pomer medzi počtom zákrut a časom stráveným pri ich cestovaní, to znamená, v čase δt, potom bude frekvencia:

F = n/Δt

Ako kolo (n = 1) sa pohybuje v čase t (obdobie), je k dispozícii nasledujúci vzťah:

F = 1/t

To znamená, že pri rovnomernej rotácii sa uhlová rýchlosť týka frekvencie prostredníctvom vzťahu:

Ω = 2π ・ f

Vzťah medzi uhlovou rýchlosťou a lineárnou rýchlosťou

Lineárna rýchlosť vložka, Je to kvocient medzi cestovanou vzdialenosťou a časovým obdobím, ktoré sa používa na jeho cestovanie. Na obrázku 2 je prevezená vzdialenosť dĺžka oblúka δs. 

Oblúk AS je úmerný uhlu prechádzajúcemu δϕ a rádio R, čím spĺňa nasledujúci vzťah:

ΔS = R ・ ϕ

Kedykoľvek sa meria ϕ v radiánoch.

Ak rozdelíme predchádzajúci výraz medzi časové obdobie Δt, získame:

(Δs/Δt) = r ・ (δϕ/Δt)

Prvým členom je lineárna rýchlosť a kvocient druhého člena priemerná uhlová rýchlosť:

Môže vám slúžiť: Mount Olympus (Mars)

v = r ・ Ω

Vyriešené cvičenia

-Cvičenie 1

Špičky lopatiek ventilátora strechy znázornené na obrázku 1 sa pohybujú rýchlosťou 5 m/s a čepele sú 40 cm polomeru.

Pri výpočtu týchto údajov: i) Priemerná uhlová rýchlosť kolesa, ii) počet zákrut, ktoré koleso dáva v druhej, iii) perióda v sekundách.

Riešenie 

i) Lineárna rýchlosť je V = 5 m/s.

Rádio je r = 0,40 m.

Zo vzťahu medzi lineárnou rýchlosťou a uhlovou rýchlosťou vyčistíme druhé:

v = r ・ Ω => Ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s

ii) Ω = 2π ・ f => f = Ω / 2π = (12,57 rad / s) / (2π rad) = 2 otáčky / s

iii) t = 1 / f = 1 / (2 otáčky / s) = 0,5 s za kolo.

-Cvičenie 2

Prechádzka hračky sa pohybuje na kruhovej dráhe polomeru 2 m. Pri 0 s je jeho uhlová poloha 0 rad, ale po čase je jeho uhlová poloha

φ (t) = 2 ・ t .

S týmito údajmi 

i) Vypočítajte priemernú uhlovú rýchlosť v nasledujúcich časových intervaloch [0S, 0.5s]; [0.5s, 1.0S]; [1.0, 1.5s] a nakoniec v období [0.0, 1.5s]. 

ii) na základe výsledkov časti I) čo sa dá povedať o pohybe?

iii) Stanovte priemernú lineárnu rýchlosť v rovnakom časovom období oddielu I)

iv) Nájdite uhlovú rýchlosť a lineárnu rýchlosť pre akýkoľvek okamih.

Riešenie 

i) Priemerná uhlová rýchlosť je daná nasledujúcim vzorcom:

Pokračujeme v výpočte prejdeného uhla a v každom intervale uplynulo časové obdobie.

Interval 1: ϕ = ϕ (0.5s) - ϕ (0.0s) = 2 (rad/s)*0.5s - 2 (rad/s)*0.0S = 1.0 RAD

                   Δt = 0.5s - 0.0S = 0.5s

Môže vám slúžiť: BTU (tepelná jednotka): rovnocennosti, použitia, príklady

                   Ω = ϕ/Δt = 1.0rad/0.5S = 2.0 rad/s

Interval 2: ϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad/s)*1.0S - 2 (rad/s)*0.5S = 1.0 RAD

                   Δt = 1.0S - 0.5S = 0.5s

                   Ω = ϕ/Δt = 1.0rad/0.5S = 2.0 rad/s

Interval 3: ϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*1.0S = 1.0 RAD

                   Δt = 1.5s - 1.0S = 0.5s

                   Ω = ϕ/Δt = 1.0rad/0.5S = 2.0 rad/s

Interval 4: ϕ = ϕ (1.5s) - ϕ (0.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*0.0S = 3.0 RAD

                   Δt = 1.5s - 0.0S = 1.5s

                   Ω = ϕ/Δt = 3.0rad/1.5S = 2.0 rad/s

ii) Vzhľadom na predchádzajúce výsledky, v ktorých bola vypočítaná priemerná uhlová rýchlosť v rôznych časových intervaloch, sa vždy dosiahne rovnaký výsledok. Zdá sa, že to naznačuje, že ide o rovnomerný pohyb kruhu. Tieto výsledky však nie sú presvedčivé.

Spôsob, ako zabezpečiť záver, je vypočítať priemernú uhlovú rýchlosť pre ľubovoľný interval [t, t -t)

                                     Δt = t ' - t

                                     Ω = ϕ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

To znamená, že hračkárska prechádzka má konštantnú priemernú uhlovú rýchlosť 2 rad/s v akomkoľvek uvažovanom časovom období. Ale môžete ísť ďalej, ak sa vypočíta okamžitá uhlová rýchlosť:

Toto sa interpretuje ako hračkársky automobil má vždy konštantnú uhlovú rýchlosť = 2 rad/s.

Odkazy

1. Giancoli, D. Fyzika. Zásady s aplikáciami. 6. vydanie. Sála. 30-45.
2. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa. 117.
3. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 33-52.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Vydanie. Mexiko. Redaktori učenia sa Cengage. 32-55.
5. Wikipedia. Uhlová rýchlosť. Získané z: Wikipedia.com