Relatívny pohyb v dimenzii, v dvoch rozmeroch, cvičeniach

On relatívny pohyb častice alebo objektu je pozorovaný s ohľadom na konkrétny referenčný bod, ktorý si pozorovateľ vybral, ktorý môže byť fixovaný alebo pohybujúci sa. Rýchlosť sa vždy vzťahuje na nejaký súradnicový systém, ktorý sa používa na jeho opísanie.

Napríklad ko -pilota pohybujúceho sa auta a to, čo pohodlne spí na svojom sedadle.

postava 1. Lietadlá medzi nimi udržiavajú určitú relatívnu rýchlosť pri praktizovaní akrobacie. Zdroj: Pixabay.

Potom je pohyb vždy relatívny, ale stáva sa, že súradnicový alebo referenčný systém je zvyčajne vybraný, má svoj pôvod na zemi alebo na zemi, miesto považované za stacionárne. Týmto spôsobom sa obavy zameriavajú na opis pohybu študovaného objektu.

Je možné opísať rýchlosť spiaceho spolubratia vzhľadom na cestujúcich, ktorý cestuje v inom aute? Odpoveď je áno. Existuje sloboda zvoliť hodnotu (x_ani, a_ani, z_ani): Pôvod referenčného systému. Výber je svojvoľný a závisí od preferencie pozorovateľa, ako aj od ľahkosti, ktorú ustanovíte pre riešenie problému.

[TOC]

Relatívny pohyb v dimenzii

Keď pohyb prechádza po priamke, mobily majú rýchlosti v rovnakom smere alebo v opačnom smere, ktoré vidia pozorovateľ stojaci na zemi (T). Pohybuje sa pozorovateľ týkajúci sa mobilných telefónov? Áno, s rovnakou rýchlosťou, akú majú, ale v opačnom smere.

Ako sa pohybuje mobilný vzhľad s druhým? Ak chcete zistiť, že rýchlosti sú pridané vektor.

Môže vám slúžiť: pluto (trpaslík planéta)

-Vyriešený príklad 1

V súvislosti s zobrazeným obrázkom uveďte relatívnu rýchlosť vozidla 1 vzhľadom na auto 2 v každej situácii.

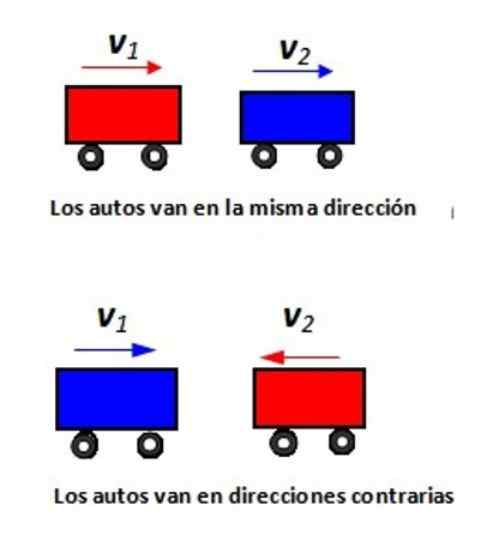Obrázok 2. Dve autá idú po priamej ceste: a) v rovnakom smere a b) v opačných smeroch.

Riešenie

K rýchlostiam priradíme kladné znamenie doprava a záporné znamenie vľavo. Ak mobil pôjde doprava o 80 km/h, cestujúci v tomto mobile vidí pozorovateľa na zemi, ktorý sa pohybuje na - 80 km/h.

Predpokladajme, že sa všetko deje pozdĺž osi x. Na nasledujúcom obrázku sa červené auto pohybuje pri +100 km/h (videné z T) a pripravuje sa na prejdenie modrého auta, ktoré cestuje pri +80 km/h (tiež viditeľné z T). S akou rýchlosťou vidíte, ako sa cestujúci priblížia k červeným autom v modrom aute?

Štítky sú: vložka _1/2 Auto 1 rýchlosť vzhľadom na 2, vložka_1/t rýchlosť automobilu vzhľadom na T, vložka_T/2 Rýchlosť tabuľky vzhľadom na 2. Pridanie vektorovo:

vložka_1/2 = vložka_1/t + vložka_T/2 = (+100 km/h - 80 km/h) X= 20 km/h X

Môžeme sa zaoberať bez zápisu vektora. Všimnite si predplatné: Vynásobenie obidvoch napravo musí získať ten vľavo.

A keď sú v opačnom smere? Teraz v_1/t = + 80 km/h a v_2/t = -100 km/h, preto v_T/2 = + 100 km/h. Cestujúci Auto Blue uvidí blížiace sa červené auto:

vložka_{1/2 =} vložka_1/t + vložka_T/2 = +80 km/h +100 km/h = 180 km/h

Relatívny pohyb v dvoch a troch rozmeroch

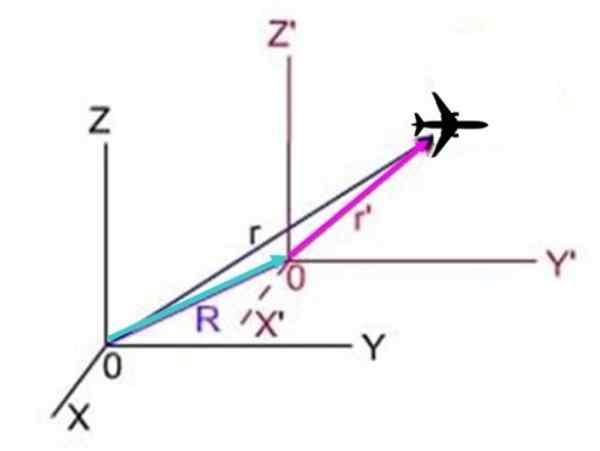
V nasledujúcej schéme, r Je to poloha roviny viditeľnej zo systému X a z, r„Je to pozícia zo systému X a z ' a R Je to poloha systému s prémiou vzhľadom na systém bez prémie. Tri vektory tvoria trojuholník, v ktorom R + r'= r, preto r'= r - r.

Obrázok 3.- Lietadlo sa pohybuje s ohľadom na dva súradnicové systémy, jeden zo systémov sa pohybuje vzhľadom na druhý.

Pretože derivát vzhľadom na čas polohy je presne rýchlosť, výsledky:

Môže vám slúžiť: parabolický záber: charakteristiky, vzorce a rovnice, príklady

vložka'= vložka - alebo

V tejto rovnici vložka„Je to rýchlosť roviny vzhľadom na systém X a z ', vložka je rýchlosť vzhľadom na systém X a z a alebo Je to konštantná rýchlosť hlavného systému vzhľadom na systém bez poistného.

-Cvičenie vyriešené 2 

Lietadlo je v severnom smere s rýchlosťou vzhľadom na vzduch 240 km/h. Zrazu začína vyfúknuť vietor zo západu na východ rýchlosťou 120 km/ podľa Zeme.

Nájdite: a) Rýchlosť lietadla vzhľadom na Zem, b) odchýlka, ktorú prežíva pilot c) korekcia, ktorú musí pilot urobiť, aby bol schopný ukazovať priamo na sever a novú rýchlosť vzhľadom na pôdu, raz Korekcia bola vykonaná.

Riešenie

a) Nasledujúce prvky sú: rovina (A), Zem (T) a vietor (V).

V súradnicovom systéme, v ktorom je Sever + a západný smer je + x, sú dané rýchlosti a ich príslušné štítok (predplatné):

vložka _Av = 240 km/h (+a); vložka _V/t = 120 km/h (+X); vložka _A/t = ?

Adekvátne vektorový súčet je:

vložka _A/t = vložka _Av + vložka _V/t = 240 km/h (+a) + 120 km/h (+X)

Veľkosť tohto vektora je: vložka _A/t = (240 ²+ 120²)^1/2 km/h = 268.3 km/h

b) 9 = arctg (v _Av / v _V/t) = arctg (240/120) = 63.4. severne od východu alebo 26.6. severovýchod.

c) Ak chcete s týmto vetrom pokračovať na sever, musíte nasmerovať luk lietadla na severozápad, takže vietor tlačí priamo na sever. V tomto prípade bude rýchlosť lietadla pozorovaná zo zeme v +a zatiaľ čo rýchlosť lietadla vzhľadom na vietor bude severozápadná (nemusí to byť nevyhnutne 26.6.).

Môže vám slúžiť: Bernoulli veta

Autor: Pythagoras Theorrem:

vložka _A/t = (240 ²- 120²)^1/2 km/h = 207.8 km/h

a = arctg (v _V/t / v _A/t ) = arctg (120/207.8) = 30. severozápad

-Cvičenie vyriešené 3

Osoba trvá 2 minúty, kým ide chôdza po nehybnom mechanickom schodisku. Ak schodisko funguje, osoba trvá 1 minútu, kým zostúpi. Ako dlho človek chodí a chodí na schodisko?

Riešenie

Je potrebné zvážiť tri prvky: osoba (P), schodisko (E) a zem (S), ktorých relatívne rýchlosti sú:

vložka_P/e : Rýchlosť osoby vzhľadom na rebrík; vložka_JE: Rýchlosť schodiska vzhľadom na zem; vložka_P/s: Rýchlosť osoby vzhľadom na zem.

Ako je vidieť zo zeme pevným pozorovateľom, osoba, ktorá znižuje schodisko (E), má rýchlosť V _P/s daná:

vložka _P/s = vložka_P/e + vložka_JE

Pozitívny zmysel ide dole po schodoch. Byť tón  čas potrebný na chôdzu a L vzdialenosť. Veľkosť osoby v _P/s je:

vložka_P/s = L / t

tón₁ Je čas, aby ste šli dolu chôdzou so zastaveným rebríkom: v _P/e = L / t₁

A t₂ Ten, ktorý ťa vezme stále na schodisku v pohybe: V _JE = L / t₂

Kombinácia výrazov:

L / t = l / t₁ + L / t₂

Výmena numerických hodnôt a zúčtovania tón:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Potom t = 1/1.5 minút = 40 sekúnd.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fyzická séria pre vedu a inžinierstvo. Zväzok 3. Vydanie. Kinematika. 199-232.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^th. Edimatizovať. Sála. 62-64.
4. Relatívny pohyb. Uzdravené z: kurzov.Lumenarning.com
5. Wilson, J. 2011. Fyzika 10. Pearson Vzdelanie. 166-168.