Čo sú to vektory Coplanares? (S vyriešenými cvičeniami)

Ten Vektory o Coplanarios sú tí, ktorí sú obsiahnutí v rovnakom lietadle. Keď máte iba dva vektory, vždy sú to dvojkoleso.

Ak máte tri alebo viac vektorov, môže sa stať, že ktorýkoľvek z nich nie je v rovnakom lietadle ako iné, preto ich nemohli považovať. Nasledujúci obrázok ukazuje súbor koplanárov označených v tučných vektoroch Do, B, C a D:

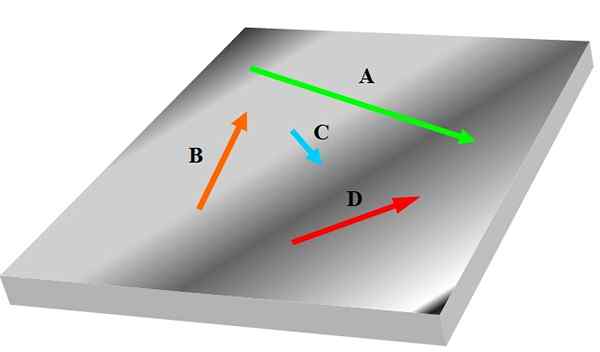postava 1. Štyri koplanáry. Zdroj: Self Made.

Vektory súvisia s správaním a vlastnosťami relevantných fyzikálnych veľkostí vo vede a inžinierstve; napríklad rýchlosť, zrýchlenie a sila.

Sila vyvoláva rôzne účinky na objekt, keď je spôsob, akým sa používa. Stále meniace sa jeden z týchto parametrov, výsledky sú značne odlišné.

V mnohých aplikáciách, a to v statickom aj dynamike, sú sily, ktoré pôsobia na tele v rovnakej rovine, preto sa považujú za koplanány.

[TOC]

Podmienky pre vektory, ktoré majú byť koplanány

Aby boli tri vektory koplanány, musia byť v rovnakom lietadle, a to sa stane, ak splnia niektorú z nasledujúcich podmienok:

-Vektory sú rovnobežné, preto sú ich komponenty proporcionálne a sú lineárne závislé.

-Váš zmiešaný produkt je neplatný.

-Ak máte tri vektory a ktorýkoľvek z nich môže byť napísaný ako lineárna kombinácia ďalších dvoch, tieto vektory sú koplanány. Napríklad vektor, ktorý je výsledkom súčtu dvoch ďalších, títo traja sú v rovnakej rovine.

Môže vám slúžiť: Voltmeter: Charakteristiky, prevádzka, čo je pre, typy

Prípadne je možné stanoviť podmienku koplanárity takto:

U v w Sú to koplanály, ak existujú tri čísla (skaláry) a, β, γ také, že aalebo + pvložka + γW = 0 S (a, β, y) odlišnými od (0, 0, 0)

Zmiešaný produkt medzi tromi vektormi

Zmiešaný produkt medzi vektormi je definovaný s tromi vektormi alebo, vložka a W, Výsledkom je skalár, ktorý je výsledkom vykonávania nasledujúcej operácie:

alebo · (vložka X W) = alebo · (v X W)

Najprv sa vyrába krížový produkt, ktorý sa nachádza v zátvorkách: vložka X W, ktorého výsledok je normálny (kolmý) vektor do roviny, v ktorej sú také vložka ako W.

Jo alebo je v rovnakej rovine ako vložka a W, Samozrejme, skalárny produkt (bodový produkt) medzi u a uvedeným normálnym vektorom musí byť 0. Týmto spôsobom sa overuje, že tri vektory sú koplanáry (ležia v rovnakej rovine).

Ak zmiešaný produkt nie je nulová, jeho výsledok sa rovná objemu paralelnepiped, ktorý má vektory alebo, vložka a W ako susedné strany.

Žiadosti

Koplanáry, súbežné a nekolineálne sily

Silné stránky súbežný Všetky sa aplikujú v rovnakom bode. Ak sú tiež koplanány, môžu ich nahradiť iba jedným, ktorý sa volá výsledná sila A má rovnaký účinok ako účinnosť pôvodných síl.

Ak je telo v rovnováhe vďaka trom Coplanares, súbežným a ne -kolineálnym (neatralemu), nazývaným sily nazývané Do, B a C, on Lamyho veta Poukazuje na to, že vzťah medzi týmito silami (veľkosti) je nasledujúci:

A / sin α = b / sen β = c / sen γ

S a, β a y ako uhly na rozdiel od aplikovaných síl, ako je to znázornené na nasledujúcom obrázku:

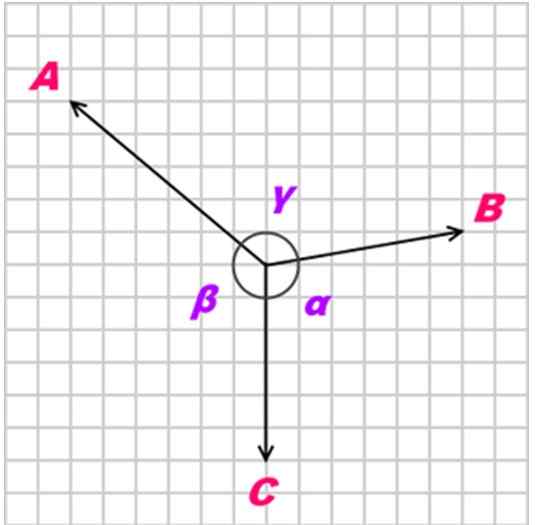Obrázok 2. Tri sily A, B a C Coplanares pôsobia na objekt. Zdroj: Kiwakwok v angličtine Wikipedia [verejná doména]

Vyriešené cvičenia

-Cvičenie 1

Nájdite hodnotu k, takže nasledujúce vektory sú koplanáry:

Môže vám slúžiť: Carnot Machine

alebo =

vložka =

W =

Riešenie

Pretože sú zložky vektorov, preto sa používajú kritériá zmiešaného produktu:

alebo · (vložka X W) = 0

Je to vyriešené ako prvé vložka X W. Vektory budú vyjadrené z hľadiska jednotkových vektorov Jo, J a klimatizovať ktoré odlišujú tri kolmé smery v priestore (široké, vysoké a hĺbkové):

vložka= 4 Jo + J + 0 klimatizovať

W= -1 Jo + 2J -1 klimatizovať

vložka X W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x j) - 2 (J x k) = 8 klimatizovať + 4 J + k -2 i = -2 Jo + 4 J + 9 klimatizovať

Skalárny produkt je teraz navrhnutý medzi U a vektorom, ktorý má výsledky z predchádzajúcej operácie, zodpovedajúca operácia na 0:

alebo · (vložka X W) = (-3 Jo + klimatizovať J + 2 klimatizovať) · (-2 Jo + 4 J + 9 klimatizovať) = 6 + 4k +18 = 0

24 + 4k = 0

Vyhľadaná hodnota je: k = - 6

Takže vektor alebo je:

alebo =

-Cvičenie 2

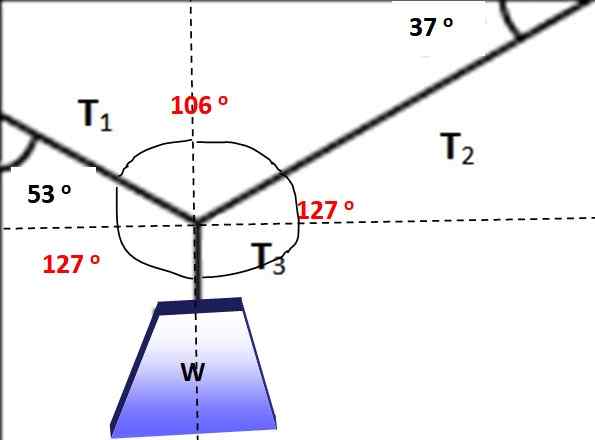
Obrázok ukazuje objekt, ktorého hmotnosť je W = 600 N, visí v rovnováhe vďaka káblom umiestneným podľa uhlov znázornených na obrázku 3. Je možné v tejto situácii aplikovať Lamyho vetu? V každom prípade nájdite veľkosti Tón₁, Tón₂ a Tón₃ čo umožňuje rovnováhu.

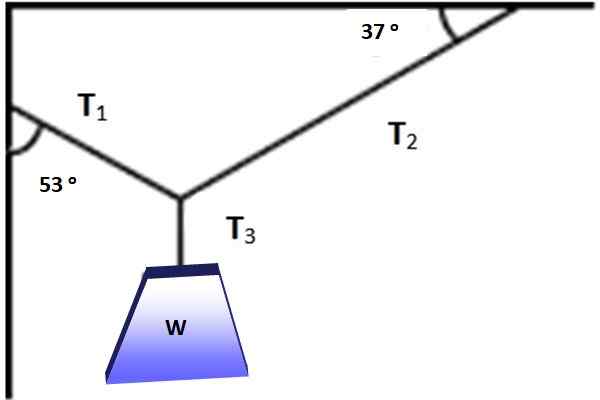Obrázok 3. Hmotnosť visí v rovnováhe pri pôsobení troch zobrazených napätí. Zdroj: Self Made.

Riešenie

Lamyho veta je použiteľná v tejto situácii, ak sa uvažuje o uzle, na ktorom sa uplatňujú tri napätia, pretože tvoria systém koplanárnych síl. Najprv sa vytvorí voľný diagram tela pre závesnú hmotnosť, aby sa určila veľkosť t_3:

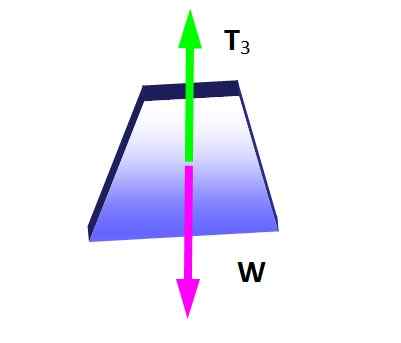Obrázok 4. Diagram voľného tela pre zavesenie hmotnosti. Zdroj: Self Made.

Z rovnovážnej podmienky Z toho vyplýva, že:

Môže vám slúžiť: Difrakcia zvuku: Čo je, príklady, aplikácie

Tón₃  = W = 600 n

Uhly medzi silami sú na nasledujúcom obrázku označené červenou farbou, je možné ľahko overiť, že jeho súčet je 360 ​​°. Teraz je možné aplikovať Lamyho vetu, pretože jedna z síl a tri uhly medzi nimi sú známe:

Obrázok 5.- V červenej uhle na nanášanie Lamyho vety. Zdroj: Self Made.

Tón₁ / Sen 127 ° = w / sen 106 °

Preto: t₁ = Sen 127 ° (W /Sen 106 °) = 498.5 n

Lamyho veta sa opäť aplikuje na vyčistenie t₂:

Tón₂ / sin 127 = t₁ / Sen 127 °

Tón₂ = T₁ = 498.5 n

Odkazy

1. Figueroa, D. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. 31-68.
2. Fyzický. Modul 8: Vektory. Získané z: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mechanika pre inžinierov. Statický. 6. vydanie. Kontinentálna redakčná spoločnosť.28-66.
4. McLean, W. Séria Schaum. Mechanika pre inžinierov: statické a dynamické. 3. vydanie. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Obnovené z: Je to.Wikipedia.orgán.