Definícia, podmienky, cvičenia nekoplanárne vektory

Ten Non -coplanares vektory Sú to tí, ktorí nezdieľajú rovnaké lietadlo. Dva voľné vektory a jeden bod definujú jednu rovinu. Tretí vektor môže alebo nemusí zdieľať toto lietadlo a ak nie, sú to nekoplalárne vektory.

Vektory neuplet nemôžu byť zastúpené v dvoch rozmerových priestoroch, ako je doska alebo list papiera, pretože niektoré z nich sú obsiahnuté v tretej dimenzii. Ak chcete ich správne zastupovať, musíte použiť perspektívu.

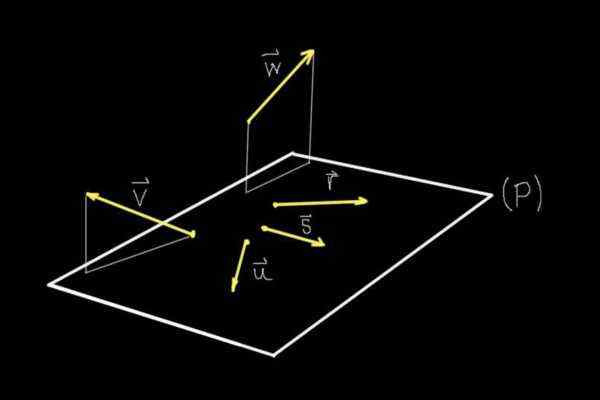postava 1. Koplanáry a nekologické vektory. (Vlastné rozpracovanie)

Ak pozorujeme obrázok 1, všetky prísne zobrazené objekty sú v rovine obrazovky, avšak vďaka perspektíve je náš mozog schopný predstaviť si lietadlo (P), ktoré vychádza z toho istého.

V tejto rovine (P) sú vektory r, siež, alebo, zatiaľ čo vektory vložka a W  Nie sú v tom lietadle.

Preto vektory r, siež, alebo Sú to koplanariy alebo koplanány medzi sebou, pretože zdieľajú rovnakú rovinu (P). Vektory vložka a W Nezdieľajú byt so žiadnym z ostatných zobrazených vektorov, preto nie sú viazané. 

[TOC]

Vektory koplanárov a rovníc rovníc

Lietadlo je jedinečne definované, ak sú v trojrozmernom priestore uvedené tri body.

Predpokladajme, že tieto tri body sú bodom Do, bod B a bod C ktoré definujú lietadlo (P). S týmito bodmi je možné postaviť dva vektory AB = U a Ac = v ktoré sú konštrukciou s lietadlom (P).

Vektorový (alebo krížový produkt) produkt týchto dvoch vektorov má za následok tretí kolmý (alebo normálny) vektor, a teda kolmý na rovinu (P):

n = u X vložka   => n ⊥ alebo  a n ⊥ vložka   => n ⊥ (P)    

Môže vám slúžiť: hmotnosť (fyzická): výpočet, jednotky, príklady, cvičenia

Akýkoľvek iný bod, ktorý patrí do lietadla (P) musí splniť tento vektor Aq byť kolmo na vektor n; To je ekvivalentné tvrdeniu, že skalárny produkt (alebo bodový produkt) n s Aq Musí to byť nula:

n • Aq = 0 (*)

Predchádzajúca podmienka je rovnocenná s tým, že:

Aq • (alebo X vložka) = 0 

Táto rovnica zaisťuje, že bod Otázka patriť do lietadla (P). 

Karteziánska rovnica lietadla

Predchádzajúcu rovnicu je možné napísať karteziánskym spôsobom. Za to píšeme súradnice bodov Do, Otázka a komponenty normálneho vektora n:

A = (a, b, c)

Q = (x, y, z)

n= (Nx, ny, nz)

Takže komponenty AQ sú:

Aq= (X-A, Y-B, Z-C)

Podmienka pre vektor Aq byť obsiahnutý v lietadle (P) Je to podmienka (*), ktorá je teraz napísaná takto:

(Nx, ny, nz) • (x-a, y-b, z-c) = 0

Výpočet bodového produktu zostáva:

nx (x-a) + ny (y-b) + nz (z-b) = 0

Ak sa vyvíja a usporiada usporiadanie, zostáva:

nx x + ny y + nz z = nx a + ny b + nz c

Predchádzajúci výraz je karteziánska rovnica roviny (P), v závislosti od komponentov normálneho vektora (P) a súradnice bodu Do čo patrí (P).

Podmienky pre tri vektory nie sú kuplanári

Ako sa stav videl v predchádzajúcej časti Aq • (alebo X vložka) = 0 zaručuje, že vektor Aq Je to coplanario a alebo a vložka.

Ak zavoláme W do vektora Aq Potom to môžeme potvrdiť:

W, alebo a vložka Sú to koplanáry, áno a iba ak W • ( alebo X vložka ) = 0.

Stav nespravodlivosti

Ak je trojitý (alebo zmiešaný produkt) produkt troch vektorov odlišný od nuly, potom tieto tri vektory nie sú krycie.

Môže vám slúžiť: politický proces: Charakteristiky, aplikácie a príklady

Jo    W • ( alebo X vložka ) ≠ 0 potom vektory u, v a w sú ne-couplanarios.

Ak sú karteziánske komponenty U, V, V a W zavedené, stav neoplnky je možné napísať takto:

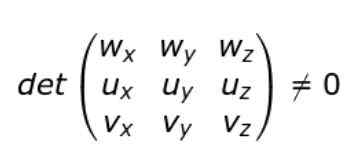To znamená, že ak je determinant matice (3 × 3), ktorých riadky sú komponentmi vektorov U, V a W, potom vektory nie sú viazané.

Triple Product má geometrickú interpretáciu a predstavuje objem paralepiped generovaných tromi non -coplanares vektormi.

Obrázok 2. Tri neotáčajúce vektory definujú paralepipedo, ktorého objem je modul s trojitým produktom. (Vlastné rozpracovanie)

Dôvod je nasledujúci; Keď sa dva z netlakových vektorov množí. 

Potom, keď sa tento vektor množí. 

Inými slovami, máte plochu rovnobežníka vygenerovanú prvými dvoma vynásobenými výškou tretieho vektora.

Alternatívne podmienky neopatrovania

Ak máte tri vektory a niektorý z nich nemožno napísať ako lineárna kombinácia ďalších dvoch, potom tri vektory sú mizerné. To sú tri vektory alebo, vložka a W Ak sú podmienky: sú to neskrývaní:

α alebo + p vložka + γ W = 0

Splní sa iba vtedy, keď α = 0, β = 0 a γ = 0.

Vyriešené cvičenia

-Cvičenie 1

Máte tri vektory

alebo = (-3, -6, 2);   vložka = (4, 1, 0) a W = (-1, 2, z)

Všimnite si, že zložka vektora Z W Nie je to známe.

Nájdite rozsah hodnôt, ktoré Z môže trvať, aby bolo zaručené, že tri vektory nezdieľajú rovnaké lietadlo.

Môže vám slúžiť: stabilná rovnováha: koncept a príklady

Riešenie 

Znovu uplatňujeme kritérium determinantu matrice vytvorenej radmi troch vektorov, týmto spôsobom zostávame: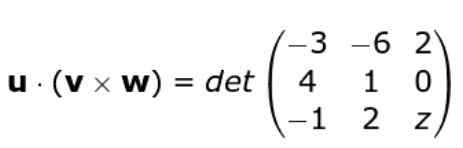Rozvíjame determinant

W • ( alebo X vložka ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Zodpovedáme tomuto výrazu pri nulovej hodnote

21 Z + 18 = 0

A vyčistíme z

Z = -18/21 = -6/7

Keby premenná Z vzala hodnotu -6/7, potom by tri vektory boli koplanány.

Takže hodnoty z, ktoré zaručujú, že vektory sú mimovládne kryty, sú tie, ktoré sú v nasledujúcom intervale:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Cvičenie 2

Nájdite objem paralelnepiped zobrazeného na nasledujúcom obrázku:

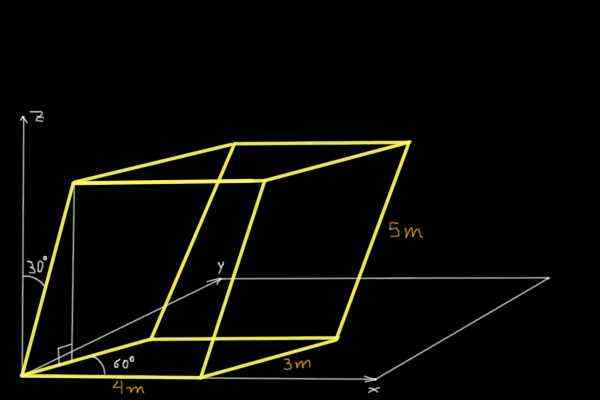
Riešenie 

Na nájdenie objemu paralelnepiped znázorneného na obrázku sa stanovia karteziánske komponenty troch nekonkurenčných vektorov, ktoré sa nachádzajú v pôvode súradníckeho systému. Prvým je vektor alebo  4 m a rovnobežne s osou X:

alebo= (4, 0, 0) m

Druhým je vektor vložka V rovine veľkosti XY 3M, ktorá sa tvorí 60 ° s osou x:

vložka= (3*cos 60 °, 3*sen 60 °, 0) = (1.5, 2.6, 0.0) m

A tretí vektor W 5 m a ktorého projekcia v rovine XY sa tvorí 60 ° s osou x, navyše w forma 30 ° s osou Z.

W= (5*hriech 30 °*cos 60 °, 5*sen 30 °*hriech 60 °, 5*sen 30 °)

Vykonali výpočty, ktoré máme: W= (1.25, 2.17, 2.5 m.

Odkazy

1. Figueroa, D. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. 31-68.
2. Fyzický. Modul 8: Vektory. Získané z: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mechanika pre inžinierov. Statický. 6. vydanie. Kontinentálna redakčná spoločnosť.28-66.
4. McLean, W. Séria Schaum. Mechanika pre inžinierov: statické a dynamické. 3. vydanie. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Obnovené z: Je to.Wikipedia.orgán