Súbežné vektory Charakteristiky, príklady a cvičenia

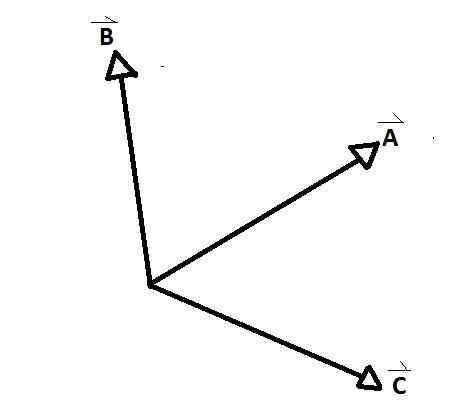
Ten súbežné vektory Sú to skupiny vektorov, ktorých sekery sa zhodujú v jednom bode a medzi nimi sa vytvárajú vnútorný a vonkajší uhol. Jasný príklad je pozorovaný v dolnom čísle, kde a, b a c sú súčasné vektory medzi sebou.

D a e na rozdiel od zvyšku nie sú. Medzi súčasnými vektormi AB, AC a CB sú tvorené uhly. Uhly vzťahov medzi vektormi sa nazývajú.

[TOC]

Charakteristika

-Majú spoločný bod, ktorý sa zhoduje s ich pôvodom: všetky veľkosti súbežných vektorov začínajú od spoločného bodu až po ich príslušné extrémy.

-Pôvod sa považuje za vektorový akčný bod: musí sa stanoviť konanie, ktoré bude priamo ovplyvnené každým zo súbežných vektorov.

-Vaša doména v lietadle a priestore je R² a r³ Súbežné vektory sú voľné pokryť celý geometrický priestor.

-Umožňuje rôzne zápisy v rovnakej skupine vektorov. Podľa študijných odvetví sú rôzne zápisy prítomné v operáciách s vektormi.

Typy vektorov

Pobočka vektorov má viacnásobné subdivízie, medzi niektorými, ktoré môžu byť vymenované: paralelné, kolmé, koplanario, zodpovedajúce, opačné a jednotné. Súbežné vektory sa objavujú na tomto zozname a rovnako ako všetci predtým vymenovaní, majú veľa aplikácií v rôznych vedách.

Sú veľmi bežné vo vektorovej štúdii, pretože predstavujú ziskovú zovšeobecnenie v operáciách s nimi. Súbežné vektory sú v lietadle aj vo vesmíre určené na súčasné použitie na reprezentáciu rôznych prvkov a študujú ich vplyv na konkrétny systém.

Vektorový zápis

Existujú rôzne spôsoby, ako reprezentovať vektorový prvok. Hlavné a najznámejšie sú:

Karteziánsky

Navrhovaný rovnakým matematickým prístupom označuje vektory so zoznamom zodpovedajúcim veľkosti každej osi (x, y, z)

A: (1, 1, -1) Priestor A: (1, 1) plán

Polárny

Slúžia iba na označenie vektorov v rovine, hoci v integrálnom výpočte je priradený hĺbkový komponent. Pozostáva z lineárnej veľkosti r a uhol vzhľadom na polárnu os Ɵ.

Môže vám slúžiť: inferenciálna štatistika: História, charakteristiky, na čo je to, príklady

A: (3, 45⁰ ) Plán A: (2, 45⁰ , 3) Priestor

Analytický

Definujte veľkosti vektora cez Verors. Verors (R&E + K) predstavujú jednotkové vektory zodpovedajúce osi X, y a

A: 3i + 2J - 3K

Sférický

Sú podobné polárnej notácii, ale s pridaním druhého uhla, ktorý sa zameta do lietadla Xy symbolizovaný Δ.

A: (4, 60^ani , π/4)

Operácie so súbežnými vektormi

Súbežné vektory sa väčšinou používajú na definovanie operácií medzi vektormi, pretože je ľahšie porovnávať prvky vektorov, keď sa vyskytujú súbežným spôsobom.

Súčet (a + b)

Cieľom súčtu súbežných vektorov je nájsť výsledný vektor Vložka_r. Čo podľa študijnej vetvy zodpovedá konečnej akcii

Napríklad: 3 reťazce sú zviazané a, b, c k škatule, každý koniec lana je v rukách subjektu. Každý z 3 subjektov musí lano vytiahnuť iným smerom ako ostatné 2.

A: (sekera, ay, az) b: (bx, by, bz) c: (cx, cy, cz)

A+b+c = (ax+bx+cx; ay+od+cy; az+bz+cz) = Vložka_r

Políčka sa preto môže pohybovať iba jedným smerom Vložka_r bude označovať smer a zmysel posunu skrinky.

Rozdiel (a - b)

Existuje mnoho kritérií týkajúcich sa rozdielu medzi vektormi, mnohí autori sa rozhodnú vylúčiť a tvrdiť, že je stanovená iba suma medzi vektormi, kde rozdiel je súčtom opačného vektora. Pravda je, že algebraicky vektory sa dajú odpočítať.

A: (sekera, ay, az) b: (bx, by, bz)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-by); AZ + (-BZ)]

Skalárny produkt (a . B)

Tiež známy ako produkt Punto, generuje skalárnu hodnotu, ktorá môže súvisieť s niekoľkými veľkosťami podľa vetvy štúdie.

Pre geometriu označuje plochu rovnobežníka vytvorenú dvojicou súbežných vektorov pomocou metódy rovnobežníka. Pre mechanickú fyziku definuje prácu vykonanú silou F Pohybom tela na vzdialenosť ΔR.

Môže vám slúžiť: Zložená proporcionalita: Vysvetlenie, tri zložené pravidlo, cvičenia

ѡ = f . ΔR

Ako už názov napovedá, generuje skalárnu hodnotu a je definovaná takto:

Byť vektormi A a B

A: (sekera, ay, az) b: (bx, by, bz)

-Analytická forma:

( . B) = | a |.| B |.Cos θ

Kde 9 je vnútorný uhol medzi oboma vektormi

-Algebraická forma:

( . B) = (sekera.Bx + ay.od + AZ.Bz)

Vektorový produkt (a x b)

Vektor alebo bodový produkt medzi dvoma vektormi definuje tretí vektor C To má kvalitu kolmého na B a C. Vo fyzike definuje vektorový krútiaci moment τ Základný prvok rotačnej dynamiky.

-Analytická forma:

| A X B | = | A |.| B |.Hriech

-Algebraická forma:

(X b) = = (Sekera . od - ay . bx)- (sekera . BZ - AZ . bx) J + (Sekera . od - ay . bx) klimatizovať

-Relatívny pohyb: r_A/b

Základom relativity je relatívny pohyb a súbežné vektory sú základom relatívneho pohybu. Môžete odvodiť pozície, rýchlosti a relatívne zrýchlenie použitím nasledujúceho poradia nápadov.

r _A/b = r_Do - r_B    ; Relatívna poloha týkajúca sa B

vložka _A/b = v_Do - vložka_B  ; Relatívna rýchlosť úcty k B

do _A/b = a_Do - do_B  ; Relatívne zrýchlenie rešpektu k B

Príklady: Vyriešené cvičenia

Cvičenie 1

Nechajte súbežné vektory A, B a C.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Definujte výsledný vektor Vložka_r = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

Vložka_r = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

Vložka_r = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1))

Vložka_r = (-15, -11, 17)

-Definujte skalárny produkt (a . C)

( . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

( . C) = 3

-Vypočítajte uhol medzi A a C

( . C) = | a |.| C |.Cos θ, kde 9 je najkratší uhol medzi vektormi

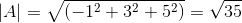
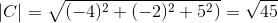
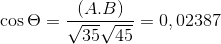
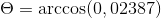
9 = 88,63⁰

 -Nájdite vektor kolmo na A a B

Z tohto dôvodu je potrebné definovať vektorový produkt medzi (-1, 3, 5) a (3, 5, -2). Ako už bolo vysvetlené, je vytvorená matica 3 x 3, kde je prvý riadok zložený zo zoznamu jednotkových vektorov (I, J, K). Potom je druhý a tretí riadok tvorený vektormi, ktoré sa majú prevádzkovať, rešpektujúc prevádzkový poriadok.

Môže vám slúžiť: desatinná notácia

(X b) = = [(-1) . 5 - (3 . 3)] Jo  - [(-1) . (-2) - (5 . 3)] J + [(-1) . 5 - (3 . 3)] klimatizovať

(X b) = (-5 - 9) Jo - (2 - 15) J + (-5 - 9) klimatizovať         

(X b) =  -14 I + 13 J - 14 K

Cvičenie 2 

Let V_do a v_b Rýchlostné vektory A a B. Vypočítajte rýchlosť B z a.

Vložka_do = (3, -1, 5) V_b = (2, 5, -3)

V tomto prípade sa požaduje relatívna rýchlosť B z Vložka_B/a

Vložka_B/a = V_B - Vložka_Do

Vložka_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

Toto je veloc vektor B videný z a. Kde nový vektor rýchlosti B je opísaný odkazom na pozorovateľa umiestneného v A a pohybom rýchlosťou a.

Navrhované cvičenia

1 konštrukcia 3 vektorov A, B a C, ktoré sú súčasné a spájajú 3 operácie medzi nimi prostredníctvom praktického cvičenia.

2 -vektory a: (-2, 4, -11), b: (1, -6, 9) a C: (-2, -1, 10). Nájdite kolmé vektory: A a B, C a B, súčet A + B + C.

4-determínové 3 vektory, ktoré sú navzájom kolmé, bez ohľadu na súradnicové osi.

5 Definujte prácu vykonanú silou, ktorá zdvíha 5 kg bloku, od spodnej časti hlbokej studne 20 m.

6-Swamker Algebraic, že ​​odčítanie vektorov sa rovná súčtu opačného vektora. Zdôvodnite svoje postuláty.

7-Denote vektor vo všetkých zápisoch vyvinutých v tomto článku. (Karteziánsky, polárny, analytický a sférický).

8-Magnetické sily vyvíjané na magnet, ktorý spočíva na stole, sú dané nasledujúcimi vektormi; V: (5, 3, -2), t: (4, 7, 9), h: (-3, 5, -4). Určite, v akom smere sa magnet pohybuje, ak všetky magnetické sily pôsobia súčasne.

Odkazy

1. Euklidovská geometria a transformácie. Clayton W. Vyhnúť sa. Couer Corporation, 1. januára. 2004
2. Ako vyriešiť Aplikáciu problémov s matematikami L. Moiseiwitsch. Couer Corporation, 10. apríla. 2013
3. Základné koncepty geometrie. Walter Prenowz, Meyer Jordan. Rowman a Littlefield, 4. októbra. 2012
4. Vektory. Rocío Navarro Lacoba, 7. júna. 2014
5. Lineárna algebra. Bernard Kolman, David R. Kopec. Pearson Education, 2006