Kolineálne vektory

Vysvetľujeme, čo sú kolineálne vektory, systém Colineal Vectors a uvádzame niekoľko príkladov

Aké sú vektory Collineal?

Ten Kolineálne vektory Sú jedným z troch typov existujúcich vektorov. Toto sú vektory, ktoré sú v rovnakom smere alebo akcii. To znamená nasledujúce: Dva alebo viac vektorov budú kolineal, ak existuje prípad, že sú usporiadané v riadkoch, ktoré sú navzájom rovnobežné.

Vektor je definovaný ako veľkosť aplikovaná na telo a je charakterizovaný smerom, zmyslom a mierkou. Vektory sa nachádzajú v rovine alebo vo vesmíre a môžu byť rôznych typov: kolineálne vektory, súbežné vektory a paralelné vektory.

Kedy sú tam kolineal vektory?

Vektory sú kolineálne, ak je línia pôsobenia jedného presne rovnaká línia pôsobenia všetkých ostatných vektorov, bez ohľadu na veľkosť a smer každého z vektorov.

Vektory sa používajú ako reprezentácie v rôznych oblastiach, ako je matematika, fyzika, algebra a tiež v geometrii, kde vektory sú kolineálne iba vtedy, keď je ich smer rovnaký, bez ohľadu na to, že ich význam nie je.

Príklady kolineálnych vektorov

• Dva alebo viac vektorov sú kolineálne, ak je vzťah medzi súradnicami rovnaký.

Príklad 1

Máte vektory m = m_x; m_y a n = n_x; N_. Toto sú kolineárne, ak:

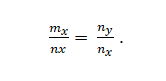
Príklad 2

Je možné určiť, či vektory j = 3,6,15 a p = 1,2,5 sú kolineárne prostredníctvom vzťahu ich súradníc, ktoré musíte navzájom úmerné; to znamená: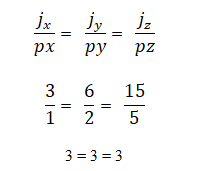

• Dva alebo viac vektorov sú kolineálne, ak sa násobenie produktu alebo vektora rovnajú nule (0). Je to tak preto, že v súradnicovom systéme je každý vektor charakterizovaný svojimi príslušnými súradnicami, a ak sú navzájom úmerné, vektory budú kolineárne. Toto je vyjadrené takto:

Môže vám slúžiť: ekvivalentné sady: Čo sú, vysvetlenie, príklady

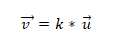
Príklad 1

Máte vektory a = (10, 5) a b = (6, 3). Aby sa určilo, či sú kolineal, uplatňuje sa určujúca teória, ktorá stanovuje rovnosť krížových produktov. Týmto spôsobom musíte:

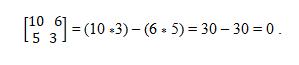
Kolineálny vektorový systém

Kolineálne vektory sú graficky znázornené pomocou smeru a smeru týchto - s ohľadom na to, že tieto musia prejsť bodom aplikácie - a modulom, ktorý je špecifickou stupnicou alebo dĺžkou.

Kolineálny vektorový systém sa tvorí, keď dva alebo viac vektorov pôsobia na objekt alebo telo, ktoré predstavujú silu a pôsobia rovnakým smerom.

Napríklad, ak sa na telo aplikujú dve kolineálne sily, výsledná jedna z nich bude závisieť iba od zmyslu, v ktorom konajú. Existujú tri prípady, ktoré sú:

Kolineálne vektory s opačnými zmyslami

Výsledkom dvoch kolineálnych vektorov sa rovná ich súčtu:

R = ∑ f = f₁ + F_2.

Príklad

Ak dve sily F konajú na vozíku₁ = 40 n a f₂ = 20 N v opačnom smere (ako je znázornené na obrázku), výsledok je:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

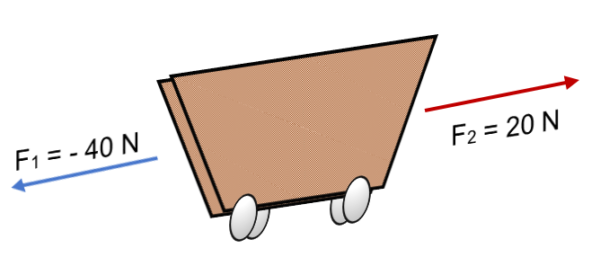Negatívny znak vyjadruje, že telo sa presunie doľava, s silou rovnajúcou sa 20 n.

Kolineálne vektory v rovnakom zmysle

Rozsah výslednej sily sa bude rovnať súčtu kolineálnych vektorov:

R = ∑ f = f₁ + F_2.

Príklad

Ak dve sily F konajú na vozíku₁ = 35 n a f₂ = 55 N V rovnakom smere (ako je znázornené na obrázku), výsledok je:

R = ∑ f = 35 n + 55n.

R = 90 n.

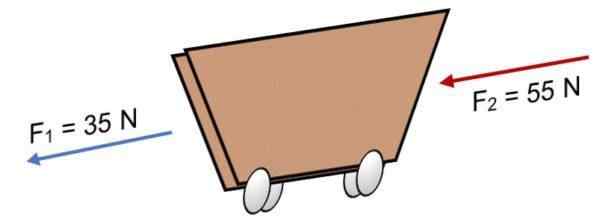
Pozitívny výsledok naznačuje, že vektory Collineal pôsobia vľavo.

Môže vám slúžiť: Pravidlo T: Charakteristiky, takže je to príklady

Kolineálne vektory s rovnakými veľkosťami a opačnými zmyslami

Výsledok dvoch vektorov Collineal sa bude rovnať súčtu kolineárnych vektorov:

R = ∑ f = f₁ + F_2.

Pretože sily majú rovnakú veľkosť, ale v opačnom smere -to znamená, že jeden bude pozitívny a ďalší negatívny -pridaním týchto dvoch síl sa výsledok bude rovnať nule.

Príklad

Ak dve sily F konajú na vozíku₁ = -7 n a f₂ = 7 n, ktoré majú rovnakú veľkosť, ale v opačnom smere (ako je znázornené na obrázku), výsledkom je:

R = ∑ f = (-7 n) + 7n.

R = 0.

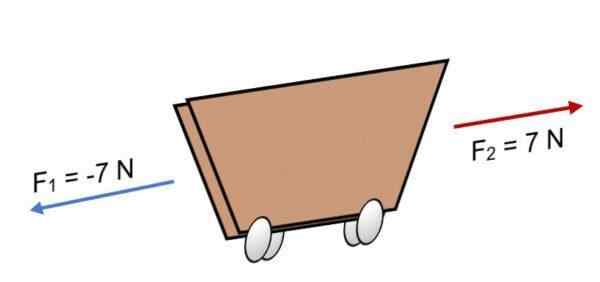
V dôsledku výsledku sa rovná 0, znamená to, že vektory si navzájom rovnováhy, a preto je telo v rovnováhe alebo odpočinku (nebude sa pohybovať).

Rozdiel medzi kolineálnymi a súbežnými vektormi

Kolineálne vektory sa vyznačujú tým, že majú rovnaký smer na rovnakom riadku, alebo preto, že sú rovnobežné s čiarom; To znamená, že sú to paralelné vektory riaditelia riadkov.

Pokiaľ ide o ich časť, sú súčasné vektory definované, pretože sú v rôznych činnostiach, ktoré sú zachytené v jednom bode.

Inými slovami, majú rovnaký bod pôvodu alebo príchodu -bez ohľadu na ich modul, význam alebo smer -formovanie uhol medzi nimi.

Súbežné vektorové systémy sú vyriešené matematickými alebo grafickými metódami, ktoré sú metódou rovnobežníka síl a metódou polygónu sily. Cez nich bude stanovená hodnota výsledného vektora, ktorý naznačuje smer, v ktorom sa telo bude pohybovať.

Hlavným rozdielom medzi kolineárnymi a súbežnými vektormi je v podstate hranica akcie, v ktorej konajú: Collineals konajú v rovnakej línii, zatiaľ čo súbežné v rôznych.

Môže vám slúžiť: Systém rovníc: Metódy riešenia, príklady, cvičenia

To znamená, že kolineárne vektory pôsobia v jednej rovine, „x“ alebo „y“; A súbežný akt v oboch lietadlách, počnúc rovnakým bodom.

Kolineálne vektory nie sú na jednom mieste, ako to robia súbežné, pretože sú navzájom rovnobežné.

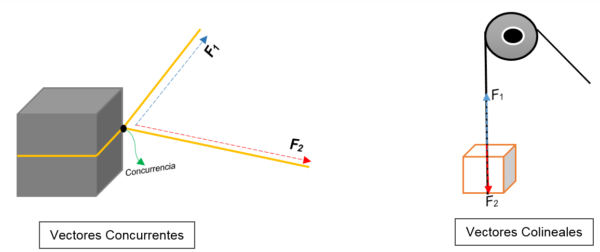
Na ľavom obrázku vidíte blok. Je zviazaný lanom a uzol ho rozdeľuje na dva; Ak sa nachádza smerom k rôznym orientáciám a s rôznymi silami, blok sa posunie smerom k rovnakému smeru.

Dva vektory sú reprezentované v jednom bode (blok), bez ohľadu na ich modul, smer alebo smer.

Na druhej strane, na pravom obrázku sa objaví kladka, ktorá zdvihne škatuľu. Lano predstavuje líniu akcie; Keď sa zastavia, na ňu konajú dve sily (vektory). Obaja majú rovnaký smer, ale v opačných zmysloch; V jednom okamihu sa nezhodujú.