Vektorové charakteristiky a vlastnosti, prvky, typy, príklady

Ten vektory Sú to matematické entity, ktoré majú veľkosť pozitívny. Takéto charakteristiky sú veľmi vhodné na opis fyzikálnych množstiev, ako sú rýchlosť, sila, zrýchlenie a mnoho ďalších.

S vektormi je možné vykonávať operácie, ako je súčet, odčítanie a produkty. Rozdelenie nie je definované pre vektory a pokiaľ ide o produkt, existujú tri triedy, ktoré opíšeme neskôr: skalárny alebo bodový produkt, vektor alebo krížový produkt a produkt skalára pre vektor.

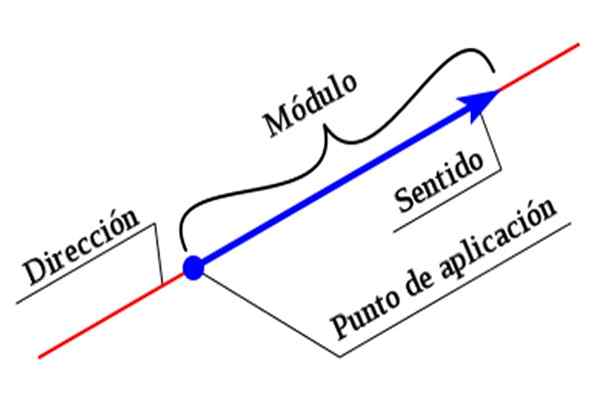postava 1. Prvky vektora. Zdroj: Wikimedia Commons.

Na úplné opísanie vektora je potrebné uviesť všetky jeho charakteristiky. Veľkosť alebo modul je numerická hodnota sprevádzaná jednotkou, zatiaľ čo smer a význam sú stanovené pomocou súradníckeho systému.

Pozrime sa na príklad: Predpokladajme, že lietadlo letí z jedného mesta do druhého rýchlosťou 850 km/h v smere. Tu máme úplne zadaný vektor, pretože veľkosť je k dispozícii: 850 km/h, zatiaľ čo smer a význam sú NE.

Vektory sú zvyčajne graficky reprezentované orientovanými segmentmi čiary, ktorých dĺžka je úmerná veľkosti.

Zatiaľ čo na špecifikáciu smeru a významu je potrebná referenčná čiara, ktorá je zvyčajne horizontálnou osou, hoci sever je možné považovať aj za referenciu, je to prípad rýchlosti roviny:

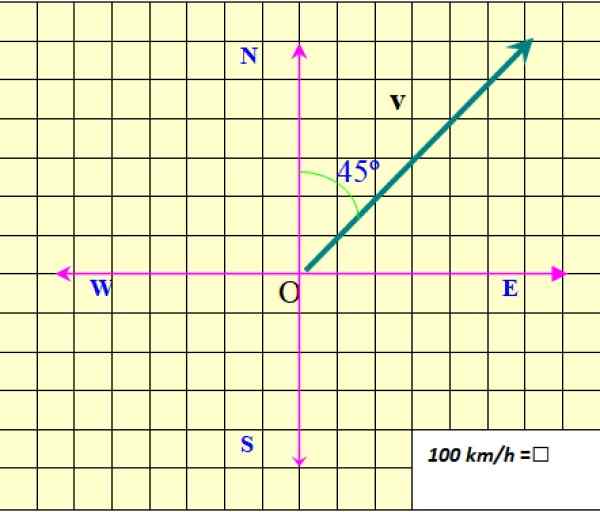Obrázok 2. Rýchlostný vektor. Zdroj: f. Zapata.

Obrázok ukazuje rýchlostný vektor roviny, ktorý je označený ako vložka v výrazný, na rozlíšenie od skalárneho množstva, ktoré vyžaduje iba číselnú hodnotu a špecifikovať určitú jednotku.

[TOC]

Prvky vektora

Ako sme už povedali, vektorové prvky sú:

-Veľkosť alebo modul, niekedy tiež nazývaná absolútna hodnota alebo vektorový štandard.

-Osloviť

-Zmysel

V príklade na obrázku 2 modul modulu vložka Je 850 km/h. Modul je označený ako V bez tučného alebo ako |vložka|, Kde pruhy predstavujú absolútnu hodnotu.

Adresa vložka je špecifikovaný s ohľadom na sever. V tomto prípade je 45 ° na sever od východu (45 ° NE). Nakoniec špička šípky informuje o smerovaní vložka.

V tomto príklade bol vektorový pôvod nakreslený zhodujúcim sa s pôvodom alebo súradnicovým systémom, je to známe ako Prepojený vektor. Na druhej strane, ak pôvod vektora nezodpovedá pôvodu referenčného systému, hovorí sa, že je to vektor.

Je potrebné poznamenať, že na úplné určenie vektora musia byť tieto tri prvky uvedené, inak by opis vektora bol neúplný.

Obdĺžnikové komponenty vektora

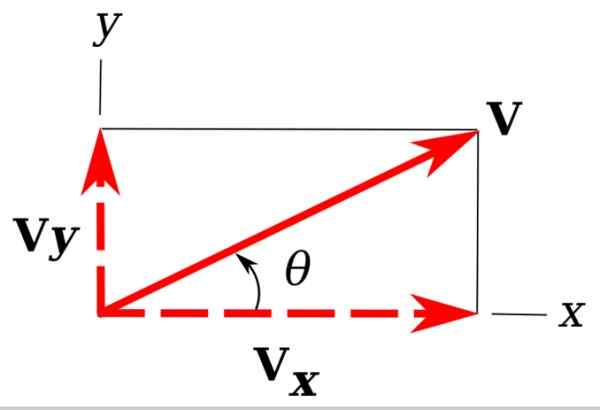Obrázok 3. Obdĺžnikové komponenty vektora v rovine. Zdroj: Wikimedia Commons. Unther [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Na obrázku máme späť náš príklad vektora vložka, To je v lietadle Xy.

Je ľahké si všimnúť, že v projekciách V na súradniciach X a Y určujú pravý trojuholník. Tieto projekcie sú vložka_a a vložka_X a nazývajú sa obdĺžnikové komponenty vložka.

Spôsob, ako označiť vložka Prostredníctvom svojich obdĺžnikových komponentov je to takto: vložka = X, vložka_a>. Tieto štvorcové zátvorky sa používajú namiesto zátvoriek na zdôraznenie skutočnosti, že ide o vektor a nie bod, pretože v tomto prípade by sa použili zátvorky.

Môže vám slúžiť: James Chadwick: Životopis, atómový model, experimenty

Ak je vektor v trojrozmernom priestore, je potrebný ďalší komponent, takže:

vložka = X, vložka_a, vložka_z>

Poznanie obdĺžnikových komponentov sa vypočíta rozsah vektora, čo zodpovedá nájdeniu hypotenusu pravého trojuholníka, ktorého nohy sú vložka_X a vložka_a,. Prostredníctvom vety Pythagory to vyplýva, že:

|vložka|² = (v_X)² +  (v_a)²

Polárna forma vektora

Keď je známa veľkosť vektora |vložka| A uhol 9, že táto forma s referenčnou osou, zvyčajne vodorovnou osou, je vektor rovnako určený. Potom sa hovorí, že vektor je vyjadrený v polárnej podobe.

V tomto prípade sa ľahko vypočítajú obdĺžnikové komponenty:

vložka_X = |vložka|.cos θ

vložka_a = |vložka|.hriech

Podľa vyššie uvedeného obdĺžnikové komponenty vektora rýchlosti vložka z lietadla by bola:

vložka_X = 850 . cos 45 ° km/h = 601.04 km/h

vložka_a = 850 . Sen 45 ° km/h = 601.04 km/h

Chlapci

Existujú rôzne typy vektorov. Existujú žily vektory, poloha, posun, sila, elektrické pole, množstvo pohybu a mnoho ďalších. Ako sme už povedali, vo fyzike existuje veľa vektorových veľkostí.

Pokiaľ ide o vektory, ktoré majú určité charakteristiky, môžeme spomenúť nasledujúce typy vektorov:

-Nulový: Jedná sa o vektory, ktorých veľkosť je 0 a ktoré sú označené ako 0. Pamätajte, že výrazné písmeno symbolizuje tri základné charakteristiky vektora, zatiaľ čo normálne písmeno predstavuje iba modul.

Napríklad o tele v statickej rovnováhe, súčet síl musí byť nulová vektor.

-Zadarmo a prepojené: Bezplatné vektory sú tie, ktorých body pôvodu a príchod sú akýmkoľvek párom bodov lietadla alebo priestoru, na rozdiel od prepojených vektorov, ktorých pôvod sa zhoduje s referenčným systémom používaným na ich opis ich opisu.

Dvojica alebo moment vyrobený niekoľkými silami je dobrým príkladom voľného vektora, pretože krútiaci moment sa nevzťahuje na určitý konkrétny bod.

-Vybavenie: Sú to dva bezplatné vektory, ktoré zdieľajú rovnaké charakteristiky. Preto majú rovnakú veľkosť, smer a význam.

-Coplanarios: Vektory, ktoré patria do tej istej roviny.

-Protiklady: vektory s rovnakou veľkosťou a smerom, ale opačné zmysly. Vektor na rozdiel od vektora vložka Je to vektor -vložka A súčet oboch je nulový vektor: vložka + (-vložka) = 0.

-Súbežný: Vektory, ktorých činnosť konania prechádzajú rovnakým bodom.

-Šmykľavka: sú tie vektory, ktorých aplikačný bod sa môže posúvať pozdĺž konkrétnej čiary.

-Kolineal: Vektory, ktoré sa nachádzajú na rovnakom riadku.

-Jednotka: Tie vektory, ktorých modul je 1.

Ortogonálne jednotky vektory

Existuje veľmi užitočný typ vektora vo fyzike nazývanej ortogonálna jednotka vektor. Vektor ortogonálnej jednotky má modul rovnajúci sa 1 a jednotky môžu byť akýmkoľvek, napríklad v rýchlosti, polohe, pevnosti alebo inom.

Existuje skupina špeciálnych vektorov, ktoré pomáhajú ľahko reprezentovať ďalšie vektory a vykonávať operácie s nimi: sú to vektory ortogonálnych jednotiek Jo, J a klimatizovať, Jednotky a kolmé na seba.

V dvoch rozmeroch sú tieto vektory nasmerované do pozitívneho zmyslu oboch osí X od osi a. A v troch rozmeroch je jednotkový vektor pridaný v smere osi z pozitívny. Sú zastúpené takto:

Môže vám slúžiť: Aká je štruktúra dokumentárneho výskumu?

Jo =

J =

klimatizovať =

Vektor môže byť reprezentovaný jednotkovými vektormi Jo, J a klimatizovať nasledovne:

vložka = v_X Jo + vložka_a J + vložka_z klimatizovať

Napríklad vektor rýchlosti vložka Z predchádzajúcich príkladov môžete písať ako:

vložka = 601.04 Jo + 601.04 J km/h

Komponent v klimatizovať Nie je to potrebné, pretože tento vektor je v rovine.

Súčet vektorov

Súčet vektorov sa objavuje veľmi často v rôznych situáciách, napríklad keď chcete nájsť výslednú silu na objekt, ktorý je ovplyvnený rôznymi silami. Ak chcete začať predpokladať, že máte dva bezplatné vektory alebo a vložka V lietadle, ako ukazuje nasledujúca ľavica:

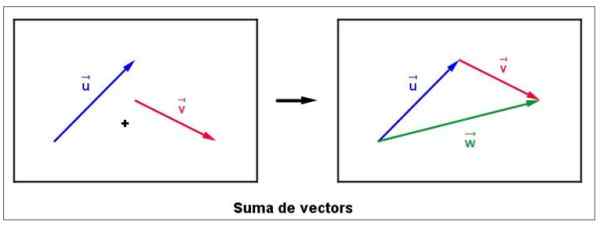Obrázok 4. Grafická suma dvoch vektorov. Zdroj: Wikimedia Commons. Lluc cabanach [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)].

Okamžite sa presunie na vektor vložka, bez úpravy jeho veľkosti, smeru alebo významu, aby vznikol alebo.

Vektor súčtu sa volá W a je nakreslený od končenia u končiac vložka, Podľa správnej postavy. Je dôležité poznamenať, že veľkosť vektora W Nie je to nevyhnutne súčet veľkostí vložka a alebo.

Ak sa v tomto ohľade dôkladne odráža, jedinou príležitosťou, keď veľkosť výsledného vektora je súčet veľkosti dodatkov, je to, keď sú obaja závislí v rovnakom smere a majú rovnaký význam.

A čo sa stane, ak vektory nie sú zadarmo? Je tiež veľmi ľahké ich pridať. Spôsob, ako to urobiť, je pridanie komponentu alebo analytická metóda.

Ako príklad, zvážme vektory nasledujúceho čísla, prvá vec je vyjadriť ich z jednej z predtým vysvetlených karteziánskych foriem:

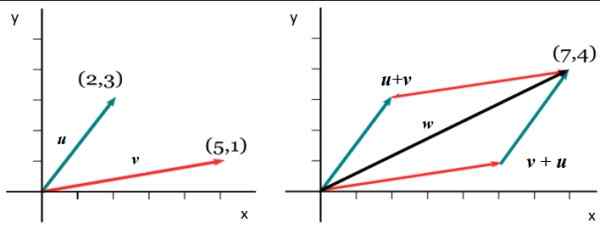Obrázok 5. Súčet dvoch prepojených vektorov. Zdroj: Wikimedia Commons.

vložka =

alebo =

Na získanie komponentu v X vektora dodáva W, Príslušné komponenty sú pridané v X z vložka a alebo: W_X = 5+2 = 7. A dostať sa W_a Dodržiava sa analogický postup: w_a = 1+3. Preto:

alebo =

Vlastnosti súčtu vektorov

-Súčet dvoch alebo viacerých vektorov má za následok iný vektor.

-Je to komutatívne, poradie dodatkov nezmení sumu, takže:

alebo + vložka = vložka + alebo

-Neutrálny prvok súčtu vektorov je nulová vektor: vložka + 0 = vložka

-Odčítanie dvoch vektorov je definované ako súčet opaku: v - u = vložka + (-or)

Príklady vektorov

Ako sme už povedali, vo fyzike je veľa vektorových množstiev. Medzi najznámejšie patrí:

-Pozícia

-Posunutie

-Priemerná rýchlosť a okamžitá rýchlosť

-Zrýchlenie

-Sila

-Pohyb

-Krútiaci moment alebo moment sily

-Impulz

-elektrické pole

-Magnetické pole

-Magnetický moment

Na druhej strane to nie sú vektory, ale lezenie:

-Čas

-Masa

-Teplota

-Zväzok

-Hustota

-Mechanická práca

-Energia

-Zahrievať

-Moc

-Napätie

-Elektrický prúd

Ostatné operácie medzi vektormi

Okrem súčtu a odčítania vektorov existujú medzi veľmi dôležitými vektormi tri ďalšie operácie, pretože vedú k novým veľmi dôležitým fyzikálnym veštiam:

-Produkt skalárneho pre vektor.

-Skalárny produkt alebo bodový produkt medzi vektormi

-A krížový alebo vektorový produkt medzi dvoma vektormi.

Produkt skalárneho pre vektor

Zvážte Newtonov druhý zákon, ktorý uvádza, že to sila F a zrýchlenie do Sú proporcionálne. Konštanta proporcionality je hmotnosť m objektu, preto:

F = m.do

Cesto je skalárne; Sila a zrýchlenie sú vektory. Pretože sila sa získa vynásobením hmotnosti zrýchlením, je výsledkom produktu skalárneho vektorom.

Môže vám slúžiť: príklady teoretického rámca

Tento typ produktu vždy vedie k vektorovi. Tu ďalší príklad: množstvo pohybu. Byť P Vektorové množstvo pohybu, vložka Vektor rýchlosti a ako vždy, m je omša:

P = m.vložka

Skalárny produkt alebo bodový produkt medzi vektormi

Umiestnili sme mechanickú prácu do zoznamu veľkostí, ktoré nie sú vektormi. Práca vo fyzike je však výsledkom operácie medzi vektormi nazývanými skalárny produkt, interný produkt alebo bodový produkt.

Byť vektormi vložka a alebo, Medzi nimi je definovaný bod alebo horolezecký produkt:

vložka∙alebo = |vložka| ∙alebo |.cos θ

Byť 9 medzi nimi uhol. Z ukázanej rovnice sa okamžite odvodí, že výsledok bodového produktu je skalárny a ak sú oba vektory kolmé, ich skalárny produkt je 0.

Späť na mechanickú prácu W, Toto je skalárny produkt medzi vektorom pevnosti F a posun vektora ℓ.

W = F∙ℓ                  

Ak sú k dispozícii vektory z hľadiska ich komponentov, je tiež veľmi jednoduchý na výpočet bodového produktu. Jo vložka = X, vložka_a, vložka_z > a alebo = X, alebo_a, alebo_z >, Bodový produkt medzi nimi je:

vložka∙alebo = vložka_X alebo_X + vložka_a alebo_a + vložka_z alebo_z

Bodový produkt medzi vektormi je preto komutatívny:

vložka∙alebo = alebo∙vložka

Krížový produkt alebo vektorový produkt medzi vektormi

Jo vložka a u sú naše dva príklady vektorov, vektorový produkt je definovaný ako:

vložka X alebo = W

Ihneď vyplýva, že krížový produkt má za následok vektor, ktorého modul je definovaný ako:

|vložka X u | = | V | . | u |. hriech

Kde θ Je to uhol medzi vektormi.

Krížový produkt preto nie je komutatívny vložka X u ≠ u X vložka. v skutočnosti vložka X U = - (u X V).

Ak sú dva príkladové vektory vyjadrené z hľadiska jednotkových vektorov, výpočet vektorového produktu sa uľahčí:

vložka = v_X Jo + vložka_a J + vložka_z klimatizovať

alebo = u_X Jo + alebo_a J + alebo_z klimatizovať

Krížové výrobky medzi jednotkovými vektormi

Krížový produkt medzi rovnakými jednotkovými vektormi je nula, pretože uhol medzi nimi je 0 °. Ale medzi rôznymi jednotkovými vektormi je uhol medzi nimi 90 ° a hriech 90 ° = 1.

Nasledujúca schéma pomáha nájsť tieto výrobky. V smere šípky má pozitívny zmysel a v opačnom smere:

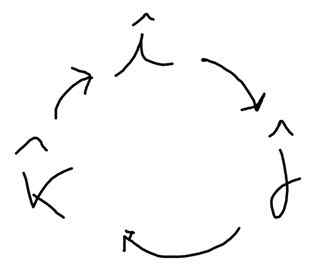
Jo X J = K, J X klimatizovať = Jo; klimatizovať X Jo = J; J X i = -k; klimatizovať X J = -Jo; Jo X klimatizovať = -J

Uplatňovanie distribučnej nehnuteľnosti, ktorá zostáva platná pre výrobky medzi vektormi plus vlastnosti jednotkových vektorov, máte:

vložka X alebo = (v_X Jo + vložka_a J + vložka_z klimatizovať) X (u_X Jo + alebo_a J + alebo_z klimatizovať) =  

= (v_aalebo_z - v_zalebo_a )Jo + (v_zalebo_X - v_Xalebo_z )J + (v_Xalebo_a - v_aalebo_X )klimatizovať

Vyriešené cvičenia

- Cvičenie 1

Vzhľadom na vektory:

vložka = -5 Jo + 4J + 1 klimatizovať

alebo = 2 Jo -3 J + 7klimatizovať

Aký by mal byť vektor W Takže suma vložka + alebo + W výsledky 6 Jo +8 J -10klimatizovať?

Riešenie

-5 Jo + 4J + 1 klimatizovať

2 Jo -3 J + 7klimatizovať

 W_X Jo + W_a J + W_z klimatizovať  +

--

6Jo + 8 J -10 klimatizovať

Preto sa musí splniť, že:

-5 +2 + w_X = 6 → w_X = 9

4-3 + W_a = 8 → w_a = 7

1 + 7 + w_z = -10 → w_z = -18

Odpoveď je: W = 9 Jo +7 J - 18klimatizovať

- Cvičenie 2

Aký je uhol medzi vektormi vložka a alebo cvičenia 1?

Riešenie

Použijeme skalárny produkt. Máme:

cos θ = vložka∙alebo / |vložka| ∙alebo|

vložka∙alebo= -10 -12+7 = -15

|vložka| = √ (-5)² +4² +1²= √42 = 6.48

|alebo| = √2² +(-3)² +7²= √62 = 7.87

Výmena týchto hodnôt:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → 9 = 107.1

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
2. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
3. Rex, a. 2011. Základy fyziky. Pearson.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
5. Serway, r., Jewett, J. 2008. Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.