Koncept lineárnej variácie, príklady, cvičenie vyriešené

Ten Lineárna variácia Vyskytuje sa medzi dvoma fyzikálnymi veľkosťami, keď je graf, ktorý ich predstavuje, priamka. Je ekvivalentné potvrdzujúce, že premenné sú v lineárnej závislosti, takže ak ho jeden z nich nazývame „y“ a druhý „x“, budú súvisieť s matematickým výrazom:

y = mx + b

V tomto vzorci sú M a B skutočné čísla. Hodnota M predstavuje sklon alebo sklon čiary - ktorá je vždy konštantná - a b je rez čiary s vertikálnou osou.

Lineárna variácia jednej veľkosti vzhľadom na druhú znamená, že jeho graf je priamka. Zdroj: Joulesergio/CC By-S (https: // creativeCommons.Org/licencie/By-SA/4.0)

Každý jav, ktorý reaguje na lineárnu variáciu, má rôzne názvy premenných, ako uvidíme v nasledujúcich príkladoch. Matematická forma rovnice je však rovnaká.

Experimentálne je možné stanoviť, ak existuje lineárny vzťah medzi dvoma veľkosťami, meraním párov hodnôt (x, y).

Získané body sú grafické v milimetrovom papieri a pozorujú sa, či majú lineárny trend, to znamená, ak existuje čiara, ktorá sa primerane prispôsobuje experimentálnym údajom.

V prvom rade je možné tento riadok nakresliť vizuálne, ale pomocou a lineárna regresia Nájdete ich analyticky, hodnoty M a B línie, ktoré najlepšie vyhovujú experimentálnym bodom.

[TOC]

Príklady lineárnej variácie

Existuje mnoho prírodných javov, ako aj nadviazané vzťahy medzi meracími vzormi, ktoré sa napríklad riadia lineárnou variáciou:

Rýchlosť v rovnomerne rozmanitom priamom pohybe

Rýchlosť v závislosti od času V (t) mobilného mobilného telefónu, ktorý sa pohybuje pozdĺž čiary s konštantným zrýchlením pri a počiatočnej rýchlosti v_ani  odlišné od 0. Tento pohyb je známy ako rovnomerne rozmanitý priamy pohyb A rýchlostná rovnica je:

Môže vám slúžiť: hustota

v (t) = v_ani + Na

Tepelná rozťažnosť

Ďalším prírodným javom, ktorého variácia je lineárna, je zvýšenie dĺžky, ktorá po zahrievaní zažije tyč alebo drôt.

Keď sa teplota akéhokoľvek objektu zvýši, jeho rozmery a toto zvýšenie závisí od zmeny teploty ΔT a množstva nazývaného množstvo nazývané množstvo nazývané lineárny dilatačný koeficient označené gréckym písmenom α:

L = l_ani + Δt

V tomto výraze l je konečná dĺžka objektu a l_ani je jeho počiatočná dĺžka.

Poloha mobilu s konštantnou rýchlosťou

Mobil s rýchlosť konštanta sa vždy pohybuje v priamke. Ak je priamka vodorovnou osou X, poloha x (t) kedykoľvek je daná:

x (t) = x_ani + VT

Kde x_ani Je to počiatočná poloha, V je rýchlosť a T je čas. Týmto spôsobom sa hovorí, že poloha X sa lineárne mení s časom t.

Postava osoby

Lekári a antropológovia môžu odhadnúť postavu osoby meraním dĺžky stehennej kosti.

Čím vyššia je osoba, tým dlhšie majú nohy, takže existujú lineárne modely na predpovedanie výšky dospelej osoby H (v palcoch), ak je dĺžka L (tiež v palcoch) jej stehennej kosti známa podľa rovnice:

H = 1.880⋅l + 32.010

Teplotné stupnice

Celsius a Fahrenheit Scales sa používajú denne na meranie teplôt. Tento posledný rozsah sa bežne používa v anglických krajinách. Existuje rovnocennosť presunúť sa z jedného na druhý:

F = (9/5) C + 32

Kde f je teplota stupňov Fahrenheita a C je teplota stupňov Celzia.

Tlak a hĺbka

Absolútny tlak P v nestlačiteľnej tekutine, ako je voda, ktorej konštantná hustota je ρ, sa líši v závislosti od hĺbky H ako:

Môže vám slúžiť: Horizontálne snímanie: Charakteristiky, vzorce a rovnice, cvičenia

P = p_ani + ρgh

Kde p_ani Je to tlak na voľný povrch kvapaliny. Ak je kvapalina v nádobe otvorenej do atmosféry, tento tlak je jednoducho atmosférický tlak P_Bankomat, Byť schopný písať potom:

P = p_Bankomat + ρgh

Atmosférický tlak na hladine mora je približne 101 kPa. Tento vzťah medzi P a H znamená, že tlak sa lineárne zvyšuje s hĺbkou.

Tlak, ktorý zažíva potápač, sa lineárne mení s hĺbkou. Zdroj: Ahmed Samy/pexels.

Cvičenie

Náklady

Mesačné náklady C pri manipulácii s automobilom zahŕňa mesačné fixné náklady C_ani Plus náklady na najazdené kilometre alebo najazdené kilometre cestovali každý mesiac. Vodič poznamenáva, že za mesiac boli náklady na správu 380 dolárov za 480 dolárov a nasledujúci mesiac to bolo 460 dolárov za 800 míľ.

Nechajte množstvo kilometrov cestovať mesačne vodičom, pričom poskytnuté údaje nájdete:

a) lineárna variácia medzi C a D.

b) Koľko by auto stálo mesačne na výlete s 1500 míľami?

c) graf C verzus d.

Roztok

Predpokladajme, že premenné majú vzťah daný:

C = c_ani + Do.d

Kde a a c_ani Sú konštantné na určenie. A je sklon čiary, ktorá graficky predstavuje vzťah medzi C a D. CO je rez s vertikálnou osou, mesačné fixné náklady, ktoré vodič musí zaplatiť iba za skutočnosť, že auto bude k dispozícii. Tu by mohli byť zahrnuté napríklad náklady na údržbu a daň.

Na jednoznačné určenie čiary je potrebné poznať jej sklon. Za to máme body:

P₁: 480 míľ, 380 dolárov

P₂: 800 míľ, 460 dolárov

Tieto body, súradníc (d, c) alebo (vzdialenosť, náklady) sú analogické s súradnicovými bodmi (x, y) karteziánskej roviny, aké zmeny sú mená. Sklon k čiare je potom daný:

Môže vám slúžiť: naklonené lietadlo

A = (c₂ - C₁)/(D₂ - d₁)

A = [(460 - 380) $ / (800 - 480) míľ] = (1/4) $ / míľa

Sklon linky predstavuje náklady na míľu týmto spôsobom:

C = c_ani + Do.D = co + (1/4).d

Určiť základné náklady c_ani Táto rovnica je prijatá a jeden z bodov, o ktorých poznáme, patrí k nej, napríklad P₁:

380 $ = c_ani + [(1/4) $ / míľa] . 480 míľ → 380 $ = c_ani + 120 dolárov

C_ani = 260 dolárov

Teraz môžeme formulovať model lineárnej variácie, ako napríklad:

C = 260 + (1/4) D

Riešenie B

Mesačné náklady na cestovanie 1500 míľ sú:

C = 260 + (1/4) x 1500 $ = 635 dolárov

Riešenie c

Graf C ako funkcia D je:

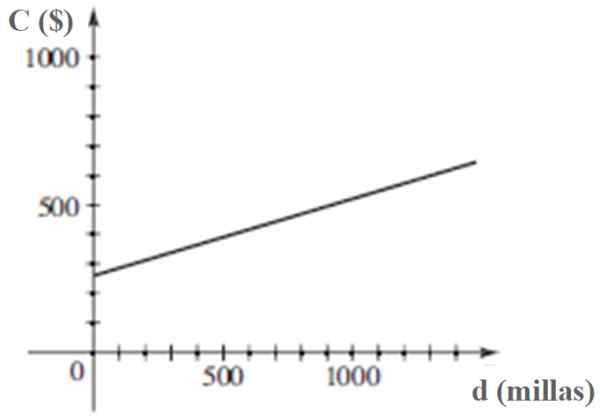Cena c manipulácie vozidla je lineárna funkcia prejdenej vzdialenosti d. Zdroj: Stewart, J. Predbežné vyfarbenie.

Odkazy

1. Plechovka. 1977. Elementárna algebra. Venezuelské kultúrne vydania.
2. Hoekenga, C. Lineárne rovnice vo vede. Získané z: VisionLearning.com.
3. Hoffman, J. Výber matematických problémov. Zväzok 2.
4. Jiménez, r. 2008. Algebra. Sála.
5. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
6. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.