Relatívna hodnota

Aká je relatívna hodnota čísla?

On relatívna hodnota čísla o číslica desatinného systému závisí od polohy, ktorú zaberá, keď je súčasťou obrázka. Preto sa hovorí, že ide o pozičnú hodnotu. Veľmi jednoduchý príklad: relatívna hodnota 1 V čísle 123, Bude to 100, Pretože 1 zaberá polohu stoviek.

Ďalší príklad: Číslo 58 je tvorené číslicami 5 a 8. Pri skúmaní tohto obrázku sprava doľava je relatívna hodnota 8 8, pretože je v polohe jednotiek a relatívna hodnota 5 je 50, pre obsadenie miesta desiatok. Číslo sa číta „päťdesiat -eight“.

Na druhej strane rovnaké číslice majú rôzne relatívne hodnoty v čísle 85, pretože si vymenili pozície. Relatívna hodnota 5 v tomto prípade je, že relatívna hodnota 8 je 80 a číslo sa vždy začína sprava doľava.

Ako nájsť relatívnu hodnotu čísla?

Všeobecný postup na nájdenie relatívnej hodnoty každej číslice je nasledujúci:

• Prvá číslica sprava doľava je v polohe jednotiek a ich hodnota sa vynásobí 1.
• Nasledujúca číslica zodpovedá desiatkam a vynásobí sa 10.
• Ďalšia poloha zodpovedá stovkám a hodnota číslice sa vynásobí 100.
• Ďalšia pozícia je tisíc, preto sa číslica vynásobí 1000.

A tak ďalej pre väčšie čísla, vynásobenie číslice zodpovedajúcim 10 napájaním: 100000, 100000 a neskôr.

Napríklad číslo 321 je možné napísať ako 3*100 + 2*10 + 1*1 alebo ekvivalent 300 + 20 + 1. V predchádzajúcom príklade je možné rýchlo vidieť, že relatívna hodnota 3 je 300, 2 je 20 a 1 1 je 1.

Môže vám slúžiť: distribučný majetok

Príklady relatívnych hodnôt

Číslo 727

Ak chcete určiť relatívnu hodnotu číslice, musíte sa riadiť nasledujúcim základným princípom písomného číslovania desatinného systému:

Akákoľvek číslica vľavo od inej predstavuje jednotku 10 -krát vyššiu a naopak: každá číslica napravo od inej, predstavuje jednotku 10 -krát menšiu. 

Napríklad číslo 727, ktorá znie „sedemsto dvadsať -seven“, pozostáva z číslic 2 a 7, so 7 opakovanými, ale zaberá rôzne pozície.

Čítanie 727 sprava doľava sa zistilo, že 7 napravo zaberá polohu jednotky, preto sa vynásobí 1:

7 x 1 = 7

A jeho relatívna hodnota je 7.

Číslica 2 v strede zaberá polohu desiatok a na nájdenie ich relatívnej hodnoty sa vynásobí 10:

2 x 10 = 20

Nakoniec na 7 až extrémnej ľavici má polohu stoviek. Potom musíte vynásobiť 100 a jeho relatívna hodnota je:

7 x 100 = 700

Všimnite si, že iba vtedy, keď číslica zaberá polohu jednotky, je to, že jej absolútna hodnota a jej relatívna hodnota sú rovnaké. Preto, ak je relatívna hodnota čísla VR a jeho absolútna hodnota je VA, všeobecný vzorec na nájdenie relatívnej hodnoty je:

VR = Absolútna hodnota VA × Hodnota svojej polohy

Obrázok môže byť napísaný ako súčet relatívnych hodnôt jej číslic, je to známe ako rozvinutý zápis. Pokračovanie s príkladom čísla 727 musíte:

727 = 700 + 20 + 7

A ak dávate prednosť použitiu právomocí 10, číslo 727 sa tiež vyjadruje rovnocenné ako:

727 = 7 ∙ 10² + 2 ∙ 10¹ + 7 ∙ 10⁰

Môže vám slúžiť: násobky 8: Čo je a vysvetlenie

Kde exponenty energie založené na 10 predstavujú polohu každej číslice a nazývajú sa Indexy. Na nasledujúcom obrázku je znázornený ďalší príklad.

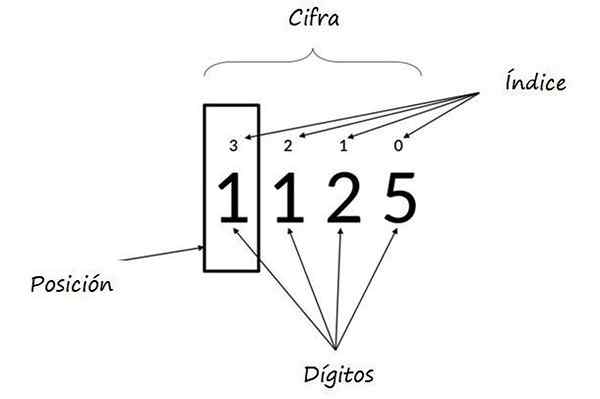V čísle 1125 je relatívna hodnota 5 5, 2 je 20, 1 je 100 a ľavá 1 v krabici je 1000. Zdroj: Wikimedia Commons.

Číslo 63

Počnúc zľava doprava je 3 v polohe jednotiek:

Relatívna hodnota 3: 3 x 1 = 3

Pokiaľ ide o 6, je to v polohe desiatok, potom:

Relatívna hodnota 6: 6 x 10 = 60

Číslo 603

Tento obrázok sa líši od predchádzajúceho, pretože hoci relatívna hodnota 0 je 0, ostatné číslice majú rôzne relatívne hodnoty. Počnúc sprava doľava ako vždy:

• Relatívna hodnota 3: 3 x 1 = 3
• Relatívna hodnota 0: 0 x 10 = 0
• Relatívna hodnota 6: 6 x 100 = 600

Číslo 630

V tomto prípade je 0 v polohe jednotiek:

• Relatívna hodnota 0: 0 x 1 = 0
• Relatívna hodnota 3: 3 x 10 = 30
• Relatívna hodnota 6: 6 x 100 = 600

Vyriešené cvičenia

Cvičenie 1

Uveďte relatívnu hodnotu podčiarknutých čísel:

a) 1209

b) 2782

c) 376

D) 3045

e) 273

Riešenie

a) číslica 1 z 1209 zastáva pozíciu tisíc alebo tisícov. Preto je jej relatívna hodnota 1000.

VR (1) = 1 x 1000 = 1000

b) 2 zaberá polohu jednotiek v 2782, preto je jej relatívna hodnota 2.

c) V 376 je 7 v polohe desiatok a:

VR (7) = 7 x 10 = 70.

d) V 3045 je 4 v polohe desiatok:

VR (4) = 4 x 10 = 40.

e) O 273 je 3 na mieste jednotiek a ich relatívna hodnota sa zhoduje s číslom číslice, to znamená:

Môže vám slúžiť: šesťuholníková pyramída

VR (3) = 3 x 1 = 3

Cvičenie 2

Napíšte najnižší počet 5 číslic, bez akýchkoľvek sa opakuje a spĺňajte nasledujúce podmienky:

a) že všetky číslice sú rôzne

b) má 7 tisíc

c) 8 je v polohe jednotiek.

Roztok

Najmenšie 5 -digitové číslo, so všetkými z nich, musí začať 1, pretože hoci 0 je nižšie, pretože prvá číslica vľavo sa nepočíta, preto požadované číslo je:

10234

Riešenie B

Poloha Millar pre 7 zodpovedá 7000, ale ako chcete najmenší možný obrázok, ktorý obsahuje 5 číslic, číslo musí začať 1, nasledovať 7 a potom 023 v zostávajúcich pozíciách, pretože sa nesmie opakovať žiadna číslica.

Preto číslo je:

17023

Riešenie c

Ako sa požaduje, aby bolo 8 v pozícii jednotiek, musí to byť na extrémne právo. Keďže je najmenším možným číslom, bez toho, aby sa opakovala každá z 5 číslic, požadované číslo je:

10238

Cvičenie 3

Vypočítajte absolútnu a relatívnu hodnotu (každého obrázku) čísla 579.

Riešenie

Má, že 579 sa rovná 5 × 100+7 × 10+9 × 1 alebo ekvivalent, rovná sa 500+70+9. Preto je relatívna hodnota 5 500, relatívna hodnota 7 je 70 a 9 je 9.

Na druhej strane, absolútna hodnota 579 sa rovná 579.

Cvičenie 4

Uveďte číslo 9.648.736, aká je relatívna hodnota 9 a prvej 6 (zľava doprava)? Aká je absolútna hodnota daného čísla?

Riešenie

Prepísaním na číslo 9.648.736 Získava sa, že je to rovnocenné

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

Alebo môžete písať ako

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

Takže relatívna hodnota 9 je 9.000.000 a relatívna hodnota prvých 6 je 600.000.

Na druhej strane, absolútna hodnota daného čísla je 9.648.736.