Oválne (geometrické postavy) Charakteristiky, príklady, cvičenia

On oválny Symetrická je definovaná ako plochá a uzavretá krivka, ktorá má dve kolmé osi symetrie - jedna hlavná a jedna menšia - a je tvorená dvoma kruhovými oblúkmi rovnajúcimi.

Týmto spôsobom môžete nakresliť pomocou kompasu a niektorých referenčných bodov na jednej zo osí symetrie. V každom prípade existuje niekoľko spôsobov, ako ho nakresliť, ako uvidíme neskôr.

postava 1. Pohľad na Rímske mleto, príklad oválnej formy v architektúre. Zdroj: Pixabay.

Je to veľmi známa krivka, pretože sa uznáva ako obrys elipsy, čo je konkrétny prípad oválu. Ale ovál nie je elipsou, aj keď sa niekedy zdá byť veľa, pretože jeho vlastnosti a vysledované sa líšia. Napríklad elipsa nie je zostavená s kompasom.

[TOC]

Charakteristika

Oval má veľmi rozmanité aplikácie: architektúra, priemysel, grafický dizajn, hodinárske a šperky sú len niektoré oblasti, v ktorých vyniká jeho použitie.

Najvýznamnejšie charakteristiky tejto dôležitej krivky sú nasledujúce:

-Patrí do skupiny technických kriviek: sleduje sa oblúky obvodov pomocou kompasu.

-Všetky jeho body sú v rovnakom lietadle.

-Chýbajú krivky alebo kravaty.

-Jeho usporiadanie je nepretržité.

-Oválna krivka musí byť mäkká a konvexná.

-Pri kreslení dotykovej čiary k oválu je všetko na rovnakej strane čiary.

-Oval podporuje dve tangenty paralelne s väčšinou.

Príklady

Existuje niekoľko metód na zostavenie oválov, ktoré si vyžadujú použitie pravidla, tímu a kompasu. Potom spomenieme niektoré z najpoužívanejších.

Môže vám slúžiť: Nerovnosť trojuholníka: demonštrácia, príklady, vyriešené cvičenia

Konštrukcia oválu sústrednými obvodmi

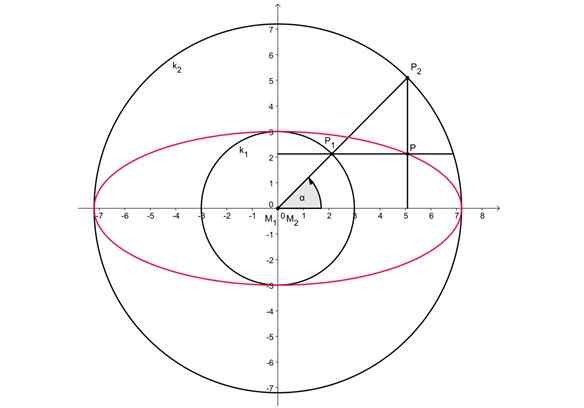Obrázok 2. Spôsob, ako nakresliť ovál cez dve sústredné obvody. Zdroj: Wikimedia Commons. Kmhkmh [cc po 3.0 (https: // creativeCommons.Org/licencie/o/3.0)]

Obrázok 2, vyššie, zobrazuje dve sústredné obvody so stredom za pôvod. Hlavná oválna os meria rovnako ako priemer vonkajšieho obvodu, zatiaľ čo menšia os zodpovedá priemeru obvodu vnútorného obvodu.

-K vonkajšiemu obvodu je pritiahnutý ľubovoľný polomer, ktorý znižuje obe obvody v bodoch P₁ A p₂.

-Potom sa premieta bod P₂ Na horizontálnej osi.

-Podobným spôsobom sa premieta bod P₁ na vertikálnej osi.

-Priesečník oboch projekčných čiar je bod P a patrí do oválu.

-Všetky body v tejto časti oválu môžu byť nakreslené týmto spôsobom.

-Zvyšok oválu je nakreslený analogickým postupom vykonávaným v každom kvadrante.

Cvičenia

Potom sa preskúmajú ďalšie spôsoby, ako zostaviť ovály.

- Cvičenie 1

Kreslite s pravidlom a kompasom ovál, známy jej hlavná os, ktorej dĺžka je 9 cm.

Riešenie

Na obrázku 3, ktorý je uvedený nižšie, výsledný oválny sa objaví v červenej farbe. Osobitná pozornosť sa musí venovať bodkovaný. Uvedíme všetky potrebné kroky na dosiahnutie konečného výkresu.

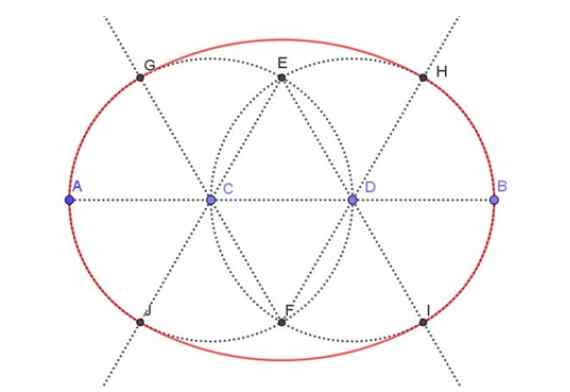Obrázok 3. Konštrukcia oválu vzhľadom na jeho hlavnú os. Zdroj: f. Zapata.

Krok 1

Nakreslite segment 9 cm AB pravidlom.

Môže vám slúžiť: Bayesova veta

Krok 2

Prestup segmentu AB, to znamená, že ho rozdelí na tri segmenty rovnakej dĺžky. Keďže pôvodný segment AB meria 9 cm, segmenty AC, CD a DB musia merať 3 cm.

Krok 3

S kompasom, vďaka čomu otvorenie C a CA nakreslí pomocný obvod. Podobne sa pomocou kompasu nakreslí pomocný obvod stredu D a rádio DB.

Krok 4

Križovatky dvoch pomocných obvodov postavených v predchádzajúcom kroku sú označené. Hovoríme tomu body e a f.

Krok 5

S pravidlom nasledujúce semifinárey.

Krok 6

Polotovary predchádzajúceho kroku znížené na dve pomocné obvody v bodoch G, H, I, J.

Krok 7

S kompasom je vyrobený v strede v F a pri otváraní (alebo rádio) FG je oblúk nakreslený Gh. Podobne je kreslený sústredený na E a s rádiom ei Ij.

Krok 8

Spojenie oblúkov Gj, Ji, IH a Hg Tvoria ovál, ktorého hlavná os meria 9 cm.

Krok 9

Pomocné body a ťahy sú vymazané (skryť).

- Cvičenie 2

Kresliť pravidlom a kompasom ovál, ktorého menšia os je známa a jej miera je 6 cm.

Riešenie

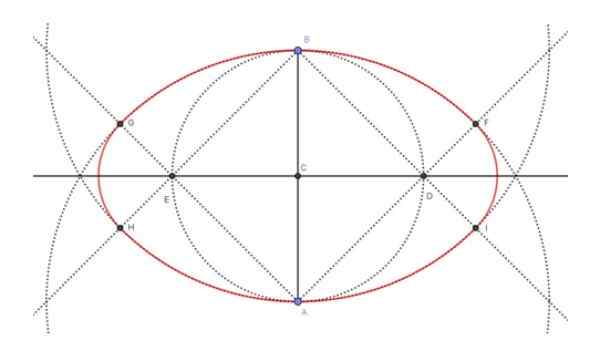Obrázok 4. Konštrukcia oválu vzhľadom na jeho menšiu os. Zdroj: f. Zapata.

Obrázok vyššie (obrázok 4) zobrazuje konečný výsledok konštrukcie oválu (v červenej farbe), ako aj medziprodukty potrebné na jeho dosiahnutie. Kroky, ktoré boli nasledované na zostavenie menšej osi oválneho 6 cm, boli nasledujúce:

Krok 1

6 cm dlhý segment AB je nakreslený pravidlom.

Môže vám slúžiť: Sada Teória: Charakteristiky, prvky, príklady, cvičenia

Krok 2

S kompasom a pravidlom je mediacia priťahovaná do segmentu AB.

Krok 3

Priesečník mediatrie so segmentom AB, vedie k stredu C segmentu AB.

Krok 4

S kompasom je nakreslený obvod Centro C a Radio CA.

Krok 5

Obvod nakreslený v predchádzajúcom kroku zachytí mediatriu AB v bodoch E a D.

Krok 6

Sú nakreslené polo -pravé [ad), [ae), [bd) a [be).

Krok 7

S kompasom sú nakreslené centrum A a Radio AB a Centro B a Radio BA Radio B a Radio BA.

Krok 8

Križovatky obvodov nakreslených v kroku 7, pričom polo -prúdi.

Krok 9

S centrom v D a Radio di oblúk, ak je nakreslený. Rovnakým spôsobom, s E a Rádiom, napr. Oblúk GH je nakreslený.

Krok 10

Únia obvodu oblúky FG, GH, HI, a ak určte vyhľadávaný ovál.

Odkazy

1. Plastový ed. Technické krivky: oválne, vajíčka a špirály. Získané z: Draw.Slovník.com.
2. Matematische basteleien. Vaječné krivky a ovály. Zdroj: Mathematische-Basteleien.
3. University of Valencia. Kužeľové a ploché technické krivky. Získané z: OCW.UV.je.
4. Wikipedia. Oválny. Obnovené z: je.Wikipedia.orgán.
5. Wikipedia. Oválny. Zdroj: In.Wikipedia.orgán.