Symboly a vzorce priemeru, ako to vytiahnuť, obvod

On priemer Je to priama čiara, ktorá prechádza stredom uzavretej plochej krivky alebo postavy v dvoch alebo troch rozmeroch a ktorá sa tiež spája s jej opačnými bodmi. Je to zvyčajne kruh (plochá krivka), kruh (plochá postava), guľa alebo priamy kruhový valec (tri rozmerové objekty).

Aj keď sa obvod a kruh zvyčajne považujú za synonymá, medzi oboma výrazmi existuje rozdiel. Obvod je uzavretá krivka, ktorá sa obklopuje kruhu, ktorá spĺňa podmienku, že vzdialenosť medzi ktorýmkoľvek z jeho bodov a stredom je rovnaká. Táto vzdialenosť nie je nič iné ako polomer obvodu. Namiesto toho je kruh plochý obrázok obmedzený obvodom.

postava 1. Priemer kolesových bicyklov je dôležitou črtou jeho dizajnu. Zdroj: Pixabay.

V prípade obvodu, kruhu a gule je priemer priamy segment, ktorý obsahuje najmenej tri body: stred plus dva body okraja obvodu alebo kruhu alebo povrch gule.

A čo sa týka priameho kruhového valca, priemer sa vzťahuje na prierez, ktorý spolu s výškou, sú jeho dva charakteristické parametre.

Priemer obvodu a kruh, symbolizovaný Ø alebo jednoducho písmenom „D“ alebo „D“, súvisí s jeho obvodom, obrysom alebo dĺžkou, ktorý je označený písmenom L:

L = π.D = π. ani

Kedykoľvek máte obvod, kvocient medzi jeho dĺžkou a jej priemerom je iracionálne číslo π = 3.14159 ..., týmto spôsobom:

π = l/d

[TOC]

Ako získať priemer?

Ak je k dispozícii výkres obvodu alebo kruhu alebo priamo kruhový objekt, napríklad mena alebo prsteň, je veľmi ľahké vziať priemer pravidlom. Jednoducho sa musíte ubezpečiť, že okraj pravidla má súčasne dva body obvodu a strednú časť toho istého.

Môže vám slúžiť: algebraic

Kaliber, vervier alebo King's Foot je veľmi vhodný na meranie vonkajších a vnútorných priemerov v minciach, obruče, krúžky, orechy, rúrky a ďalšie.

Obrázok 2. Vernier digitálne meranie priemeru mince. Zdroj: Pixabay.

Ak namiesto objektu alebo jeho kresby máte údaje ako rádio R, Potom vynásobením 2 máte priemer. A ak je známa dĺžka alebo obvod obvodu, priemer sa dá známy aj pri vôľu:

D = 2.R
D = l / π

Ďalším spôsobom, ako získať priemer, je poznať oblasť kruhu, sférický povrch, prierez valca, zakrivená plocha tohto alebo objemy gule alebo valca. Všetko záleží na tom, ktorá geometrická postava je. Napríklad priemer je zapojený do nasledujúcich oblastí a zväzkov:

-Kruhová plocha: π.(D/2)²
-Sférická plocha: 4π.(D/2)²
-Objem: (4/3) π.(D/2)³
-Priamy objem kruhového valca: π.(D/2)².H (h je výška valca)

Obrázky konštantného širokého

Kruh je plochá postava konštantnej širokej, pretože kdekoľvek vyzerá, šírka je priemer d. Existujú však aj ďalšie možno menej známe čísla, ktorých šírka je tiež konštantná.

Najprv sa pozrime, čo sa rozumie šírke obrázku: Je to vzdialenosť medzi dvoma paralelnými čiarami -podporu, ktoré sú zase kolmé na daný smer a ktoré uväznia obrázok, ako je to znázornené na ľavom obrázku:

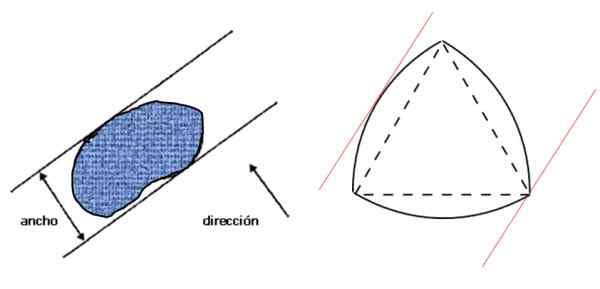Obrázok 3. Šírka akejkoľvek plochej postavy (vľavo) a trojuholníka Reuleaux, konštantná široká postava (vpravo). Zdroj: f. Zapata.

Potom vpravo je trojuholník Reuleaux, ktorý je konštantnou širokou postavou a ktorá spĺňa stav uvedený na ľavom obrázku. Ak je šírka čísla d, jeho obvod je daný Barbierovou vetou:

Môže vám slúžiť: približné meranie amorfných figúr: Príklad a cvičenie

L = π.D

Kanalizácia mesta San Francisco v Kalifornii je v tvare trojuholníka Reuleaux, pomenovaná nemeckým inžinierom Franzom Reuleauxom (1829 - 1905). Týmto spôsobom nemôžu tapas spadnúť do otvoru a minúť menej materiálu na ich výrobu, pretože ich oblasť je menšia ako oblasť kruhu:

A = (1- √3).πD² = 0.705.D²

Zatiaľ čo pre kruh:

A = π.(D/2)² = (π/4) d²= 0.785.D²

Ale tento trojuholník nie je jedinou konštantnou širokou postavou. Hovory môžu byť postavené Reuleaux polygóny s inými polygónmi, ktoré majú nepárne stránky.

Priemer obvodu

Na nasledujúcom obrázku sú prvky obvodu definované takto:

Lano: segment riadku, ktorý sa spája s dvoma bodmi obvodu. Na obrázku je lano, ktoré sa spája s bodmi C a D, ale nekonečné reťazce možno vysledovať, že jedinečné akékoľvek pár bodov obvodu.

Priemer: Je to lano, ktoré prechádza stredom a spája dva body obvodu so stredom alebo. Je to najdlhšie lano obvodu, z tohto dôvodu sa nazýva „hlavné lano“.

Rozhlas: segment linky, ktorý sa spája s centrom s akýmkoľvek bodom obvodu. Jeho hodnota, rovnako ako priemer, je konštantná.

Obvod: Je to sada všetkých bodov, ktoré sa rovná alebo.

Klonovať sa: Je definovaný ako segment obvodu vymedzeného dvoma rádiá (na obrázku nie je nakreslené).

Obrázok 4. Časti obvodu vrátane priemeru, ktorý prechádza stredom. Zdroj: Wikimedia Commons.

- Príklad 1

Zobrazený obdĺžnik meria 10 palcov vysoký, čo pri vinutí tvorí rovný kruhový valec, ktorého priemer je 5 palcov. Odpovedaj na nasledujúce otázky:

Môže vám slúžiť: vzájomne sa vylučujú udalosti: Vlastnosti a príklady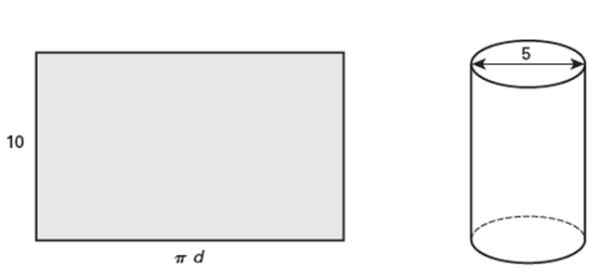Obrázok 5. Valcovaný obdĺžnik sa stáva priamym kruhovým valec. Zdroj: Jiménez, r. Matematika II. Geometria a trigonometria. Druhý. Vydanie. Pearson.

a) Aký je obrys trubice?
b) Nájdite oblasť obdĺžnika
c) Vypočítajte plochu prierezu valca.

Roztok

Obrys trubice je l = π.D = 5π plg = 15.71 plg.

Riešenie B

Oblasť obdĺžnika je Výška, Byť už vypočítaným základňou L a výška je 10 plg podľa vyhlásenia: Preto:

A = 15.71 plg x 10 plg = 157.1 plg².

Riešenie c

Nakoniec sa požadovaná oblasť vypočíta takto:

A = π.(D/2)² = (π/4) d² = (π/4) x (5 plg)²= 19.63 plg².

- Príklad 2

Vypočítajte tieňovanú oblasť na obrázku 5A. Štvorec má stranu l.

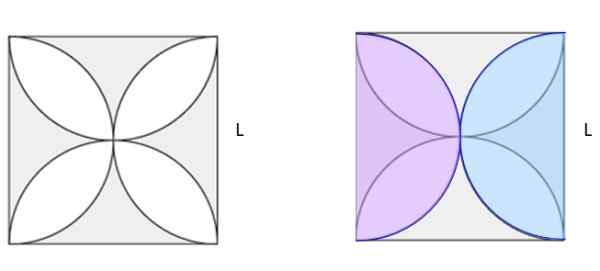Obrázok 6. Nájdite tieňovanú oblasť na ľavej postave. Jiménez, r. Matematika II. Geometria a trigonometria. Druhý. Vydanie. Pearson.

Riešenie

Na obrázku 5b boli nakreslené dva identické polkruhy veľkosti v ružových a modrých farbách, prekrývané na pôvodnom obrázku. Medzi nimi robia kompletný kruh. Ak sa vypočíta štvorec štvorca a odpočíta sa oblasť kruhu, je zatienená oblasť na obrázku 5b. A vyzerá dobre, ukázalo sa, že je to polovica tieňovanej oblasti v 5a.

-Štvorcový štvorec: L²
-Priemer polkruhu: L
-Kruhová plocha: π.(L/2)²= (π/4) l²
-Rozdiel v oblastiach = polovica tieňovanej oblasti =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 L²

-Zatienená oblasť = 2 x 0.2146 L²= 0.4292l2

Koľko priemerov má obvod?

Nekonečné priemery môžu byť nakreslené v kruhu a každý z nich meria rovnako.

Odkazy

1. Antonio. Reuleaux trojuholníky a ďalšie krivky konštantnej šírky. Získané z: Diseminátorov.com.
2. Baldor, a. 2002. Geometria plochej a priestoru a trigonometrie. Kultúrna vlastná skupina.
3. Jiménez, r. Matematika II. Geometria a trigonometria. Druhý. Vydanie. Pearson.
4. Wikipedia. Reuleaux trojuholník. Obnovené z: Je to.Wikipedia.orgán.
5. Wolfram Mathworld. Priemer. Obnovené z: Mathworld.Valfram.com.