Vysvetlíme, čo a aké sú disperzné opatrenia, a uvádzame niekoľko príkladov

Aké sú disperzné opatrenia?

Ten opatrenia alebo variácie, v štatistike, zmerajte, koľko distribúcie údajov z hodnoty centrálneho opatrenia sa pohybuje, ako je priemerný alebo aritmetický priemer. Jeho hodnota je vždy pozitívna a normálne sa líši od 0, s výnimkou identických údajov.

Ak opatrenie disperzie prinesie malú hodnotu, znamená to, že údaje sa nachádzajú veľmi blízko k priemeru, ale ak sú veľké, znamená to, že údaje sú preto viac rozptýlené od priemeru.

Opatrenia disperzie sú zo štatistického hľadiska veľmi dôležité, a to nielen ako aritmetické ukazovatele variácie údajov, ale ako neoceniteľná pomoc, keď chcete zlepšiť kvalitu, a to tak pri výrobe výrobkov, ako aj pri poskytovaní služieb.

Príkladom sú rady pozornosti v bankách. Priemerné časové oneskorenie zákazníkov, keď vytvoria jedinečný riadok a potom sú distribuované v pokladni, je rovnaké, ako keby pred každým vyrábali jednotlivé riadky.

Disperzia je však nižšia v jednom riadku, čo znamená, že individuálny čas pozornosti je veľmi podobný každému klientovi. Zákazníci vyhlásili, že sa takto cítia pohodlnejšie, aj keď priemerný čas starostlivosti je rovnaký v oboch modalitách.

Hlavné disperzné opatrenia

Hlavné sú: hodnosť, rozptyl, štandardná odchýlka a variácia koeficientu.

Rozsah

Rank R súboru údajov je definovaný na rozdiel medzi maximálnou hodnotou x_Maximálny a minimálna hodnota x_blesk celku:

Rang = r = maximálna hodnota - minimálna hodnota = x_Maximálny - X_blesk

Môže vám slúžiť: Aké sú čísla pre? 8 hlavných použití

Rozsah sa rýchlo vypočíta, ale je veľmi citlivý na extrémne hodnoty a má nevýhodu, že nezohľadňuje medziprodukty. Preto sa používa iba na počiatočnú, pomerne približnú predstavu o disperzii údajov.

Príklad hodnosti

Toto je zoznam počtu hurikánov v Atlantiku za posledných 14 rokov:

8; 9; 7; 8; pätnásť; 9; 6; 5; 8; 4; 12; 7; 8; 2

Údaje o maximálnej hodnote sú 15 a minimálna hodnota je 2, preto:

R = maximálna hodnota - minimálna hodnota = x_Maximálny - X_blesk = 15 - 2 = 13 hurikánov

Rozptyl

Toto opatrenie sa používa na porovnanie každého z údajov s priemerom množiny a vypočíta sa pridaním rozdielov, štvorcových vysokých, medzi každou hodnotou s priemerom a delením celkovým počtom hodnôt.

Byť:

-Priemer: μ

-Akákoľvek hodnota, ktorá patrí do súboru údajov: x_Jo

-Celkový počet pozorovaní: n

Označovanie rozptylu populácie ako σ², Výraz na jeho výpočet je:

A keď sa odoberie vzorka populácie, uprednostňuje sa výpočet rozptylu týmto spôsobom:

Kde sa rozptyl vzorky označil s S a priemerom X s barom, aby sa zanechalo používanie gréckych listov pre obyvateľstvo. Dôvodom rozdelenia medzi N-1, namiesto N, je, aby sa rozptyl vzorky nepodceňoval populáciu, čo sa vždy stane, keď sa rozdelí medzi n.

Na druhej strane, myšlienka štvorca každého rozdielu medzi údajmi a priemerom je zabrániť im v ich pridaní 0, pretože niektoré rozdiely budú pozitívne a iné negatívne, čo má tendenciu zrušiť sumu. Namiesto toho sú štvorce vždy pozitívne.

Môže vám slúžiť: Pravdepodobnosť frekvencie: koncept, ako sa vypočíta a príklady

Preto je rozptyl vždy pozitívny, aj keď rozdiel medzi x_Jo A priemer je negatívny a jeho hlavnou výhodou rozptylu je to, že berie do úvahy každé údaje súboru.

Má však nepríjemnosti, že jeho jednotky nie sú rovnaké ako jednotky, napríklad ak tieto pozostávajú v časoch, merané v minútach, rozptyl sady sa podá v minútach na štvorce.

Príklad rozptylu

Výpočet rozptylu vyžaduje nájdenie priemeru. Ak vezmeme údaje o čísle hurikánu, priemer sa vypočíta podľa:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 hurikány.Preto je rozptyl:

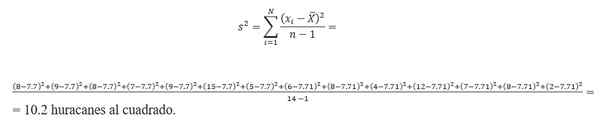
Štandardná odchýlka

Na nápravu problému nedostatku zhody medzi jednotkami je definovaná štandardná odchýlka σ, Rovnako ako druhý koreň rozptylu:

A analogicky, v prípade vzorky:

Existuje empirické pravidlo na odhad hodnoty štandardnej odchýlky súboru údajov o vzorke na základe rozsahu. Podľa tohto pravidla je štandardná odchýlka približne štvrtina R:

S ≈ R/4

Má tú výhodu, že umožňuje rýchly odhad štandardnej odchýlky, pretože operácie sú oveľa jednoduchšie.

Štandardná odchýlka je s mnohými najbežnejšie používanými disperznými opatreniami, takže stojí za to zdôrazniť jej hlavné vlastnosti:

• Štandardná odchýlka označuje, do akej miery sa médiá sťahujú
• Je to vždy pozitívne, ale môže to byť 0, ak sú všetky údaje identické
• Čím väčšia je hodnota štandardnej odchýlky, tým viac sú rozptýlené údaje
• Štandardné odchýlky sú rovnaké ako v študovanom premennej
• Jeho hodnota sa rýchlo mení, keď má jeden z údajov (alebo viac) veľmi odlišnú hodnotu ako zvyšok
• Hodnoty štandardnej odchýlky sú skreslené, to znamená, že priemery štandardnej odchýlky nie sú distribuované okolo priemeru, na rozdiel od rozptylu, ktorý nie je zavedený.

Môže vám slúžiť: acutangle trojuholník

Príklad štandardnej odchýlky

V prípade príkladu hurikánov je štandardná odchýlka:

Alebo, ak sa uprednostňuje, aby ste použili prístup štandardnej odchýlky v rozsahu, získa sa pomerne blízka hodnota:

S = 13/4 = 3.25

Koeficient variácie

Koeficient variácie je označený iniciálmi CV alebo R, v niektorých textoch, ako aj pre populáciu, ako aj pre vzorku, sa týka štandardnej a priemernej odchýlky v percentách:

O dobre:

Rovnice sú platné, pokiaľ sa priemer líši od 0.

Variačný koeficient je spravidla zaokrúhlený na jedno desatinné miesto a používa sa na porovnanie údajov z dvoch rôznych populácií.

Príklad variačného koeficientu

Čakacie doby v sekundách pre klientov banky sú zaznamenané v dvoch situáciách: keď urobia jedinečný riadok a keď urobia individuálne hodnosti pred kanceláriou pozornosti. Výsledky sú nasledujúce:

Oba súbory údajov je možné porovnávať prostredníctvom ich príslušného koeficientu variácie:

Jednotlivý riadok

• Priemer = 429 sekúnd
• Odchýlka = 28.6 sekúnd
• CV = (28.6/429) x 100 = 6.7 %

Individuálne hodnosti

• Priemer = 429 sekúnd
• Odchýlka = 109.3 sekundy
• CV = (109.3/429) x 100 = 25.5 %

Pretože táto posledná hodnota je vyššia, naznačuje to, že v časoch služieb zákazníkom existuje väčšia variabilita, keď vytvárajú individuálne rady, ako keď vytvoria jedinečný riadok, hoci priemerný čas je v každom prípade rovnaký.