A naháňačka Je to plochá postava štyroch strán, -a štvorkolatá -v ktorej sú jeho strany a vnútorné uhly rôzne dva až dva. Preto rhomboid patrí do skupiny šikmých rovnobežníkov.

Geometrické čísla sú súčasťou prírody a najmä tie, ktoré majú štyri strany, ako napríklad Rhomboid, majú veľa aplikácií v architektúre a dizajne.

postava 1. Osvetľovacie panely štadióna Allianz Arena v Mníchove v Nemecku, osvetľujú farby miestneho tímu a bieleho svetla, keď sa výber tejto krajiny hrá. Zdroj: pxhere.

Hore máme časť fasády futbalového štadióna Allianz Arena v Mníchove. Sú to panely rhomboidu, ktoré sa rozsvietia farbami miestneho tímu.

Je to preto postava s množstvom vizuálnej dynamiky, pretože na rozdiel od iných kvadrilaterálov nemá osi symetrie. Nasledujúci obrázok zobrazuje rôzne rhomboidy s rôznymi orientáciami v rovine.

Obrázok 2. Niekoľko Rhomboid s rôznymi orientáciami v rovine. Zdroj: f. Zapata.

[TOC]

Charakteristika Romboidu

Ďalej hlavné charakteristiky tejto zaujímavej geometrickej postavy:

-Číslo listu: 4.

-Počet vrcholov: 4.

-Opačné strany sú rovnaké a rovnobežné, priľahlé strany sú však nerovnaké.

-Má 4 vnútorné uhly: dva akútne (menej ako 90 °), označené gréckym písmenom a a dva tupé (nad 180 °), nazývané β (pozri obrázok 3).

-Pridaním dvoch susediacich uhlov rhomboidu sa získa 180 °, preto sú a a p Doplnkový.

-Súčet 4 vnútorných uhlov sa rovná 360 °.

-Diagonál je segment, ktorý začína od vrcholu a končí na opačnom vrchole.

-Bod, v ktorom sa nazýva diagonály pretínania rhomboidu barycenter.

-Rhomboid Diagonals majú rôzne veľkosti.

O diagonáloch rhomboidu Existujú niektoré dôležité podrobnosti, o ktorých budeme diskutovať nižšie.

Môže vám slúžiť: Činnutie riadku: vzorec a rovnice, reprezentácia, príklady

Diagonála rhomboidu

Je veľmi dôležité zdôrazniť, že diagonály rhomboidov nie sú bisektrické, to znamená, že nedarí vnútorné uhly postavy na dve rovnaké časti.

Diagonály nie sú navzájom kolmé. Môžeme ich však ľahko vypočítať pomocou kosínutej vety. Preto hlavná diagonálna D_M V Rhomboid na obrázku 3 je:

D_M = √ (a² + b² - 2.AB.cos β)

A menšie diagonálne d_m Bol by som:

D_m = √ (a² + b² - 2.AB.cos α)

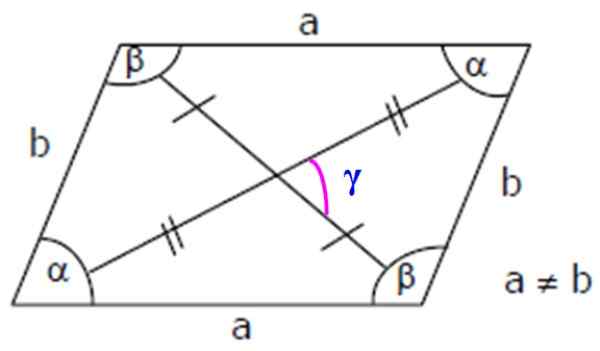Obrázok 3. Romboid prvky: boky, vnútorné a diagonálne uhly. Zdroj: Wikimedia Commons.

Dôležitý: Keďže α a p sú doplnkové, splní sa to:

hriech α = sin β

cos α = -cos β

Pri riešení cvičení sa musia zohľadniť tieto vlastnosti trigonometrických dôvodov.

Ako vytiahnuť obvod a oblasť

Ak chcete nájsť obvod a oblasť, ktorú pomenujeme bokom rhomboidu, bude to do a b. Máme tiež výšku rhomboidu, ktorá sa volá h, čo je čiara vytiahnutá z jedného z vrcholov a nasmerovaná kolmo na opačnú stranu obrázku.

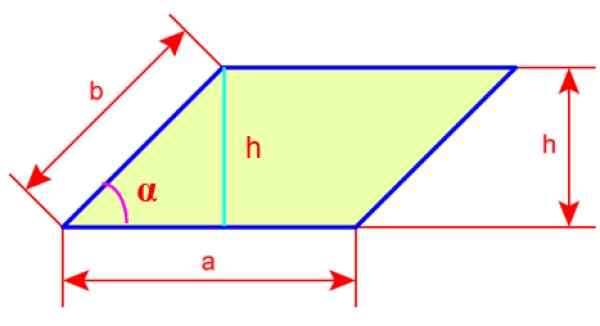Obrázok 4. Boky a výška rhomboidu. Zdroj: Wikimedia Commons.

Obvod rhomboidu

Obvod rhomboidu sa vypočíta pridaním dĺžok jej štyroch strán. Zavolajme na obvod, potom:

P = 2a + 2b

Môžeme to tiež vyjadriť prostredníctvom:

P = 2 (a+b)

Obvod, ktorý pozná výšku

Ak vyzeráme dobre, výška H je možné určiť z trojuholníka vľavo na obrázku 4. Strana B by bola hypotenus a výška h kateto na rozdiel od uhla a, preto:

Sin α = opačný / hypotenusa kateto

O dobre:

Sin α = H / B

Potom vyčistíme b:

b = h / sin α

Nahrádzame v obvode P:

P = 2 [a + (h / sin α)]

Oblasť Romboidu

Oblasť Rhomboid je miera jeho povrchu. A keďže ide o rovnobežník, jeho oblasť A je daná dobre známym výrazom:

Môže vám slúžiť: spoločný faktor pre zoskupovanie podmienok: príklady, cvičenia

A = výška základne x

Že podľa obrázkov 3 a 4 sa vyjadruje prostredníctvom:

A = a x h

Oblasť, ktorá pozná obe strany a vnútorný uhol

Pri použití základnej trigonometrie v predchádzajúcej časti nachádzame ekvivalentné výrazy pre oblasť Rhomboid:

h = b. hriech α

Potom je oblasť taká:

A = a. b. hriech α

Pripomínajúc, čo sme povedali vyššie o doplnkových uhloch, v prípade potreby môžeme nahradiť Sen α za Sen β.

Oblasť, ktorá pozná diagonály a uhol medzi nimi

Nakoniec, ak poznáme diagonály D_M a d_m, Plus uhol γ medzi nimi (pozri obrázok 3), oblasť sa môže vypočítať pomocou polo -produktu diagonálov cez lonu uvedeného uhla:

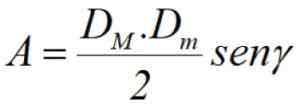
Cvičenie

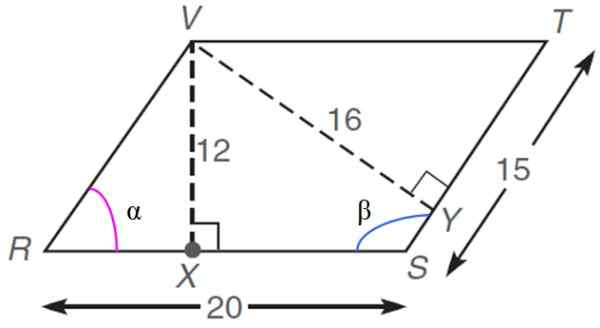
V nasledujúcom Rhomboid, ktorého rozmery sú uvedené v ľubovoľných jednotkách alebo.do., Nájsť:

a) Obvodová hodnota

b) oblasť

c) vnútorné uhly a a p

d) dĺžka segmentu RX

e) Miera každej z diagonálov

Roztok

Obvod P je:

P = 2 (a + b)

Najprv identifikujeme hodnoty A a B:

A = 20

B = 15

Nahradíme vzorec a vypočítame:

P = 2. (20 + 15) = 70 u.do.

Riešenie B

Diagram poskytuje výšku h = 12 u.A preto sa oblasť môže vypočítať pomocou vzorca:

A = a x h

A = 20 x 12 u.do.² = 240 u.do.²

Bez ohľadu na vybranú jednotku na meranie bokov a výšky je oblasť vždy vyjadrená v štvorcových jednotkách.

Rovnaký výsledok, ak sa dostanete pri výpočte oblasti s druhou výškou rhomboidu, ktorá má hodnotu 16 U.do. Naozaj:

A = 16 x 15 u.do.² = 240 u.do.²

Riešenie c

Uhol a je možné vypočítať prostredníctvom:

Môže vám slúžiť: polohové opatrenia, centrálna tendencia a disperzia

h = b. hriech α

Pretože hodnoty H a B sú známe, preto:

a = arcsen (h/b) = arcsen (12/15) = 53.13

Pamätajte si, že a a p -uhly sú doplnkové, je splnené:

a + β = 180 ° ⇒ β = 180 - 53.13. = 126.87 °

Riešenie d

Dĺžka segmentu RX sa ľahko vypočíta, pretože existuje dostatok informácií na ich nájdenie. Napríklad prostredníctvom:

Rx = rv . cos α = 15 . Cos 53.13. u.do. = 9 u.do.

Aj cez vetu Pythagoras cez obdĺžnikový trojuholník strany 15 a 12 u.na:

(Rv)² = (Rx)² + h²

Vyčistenie dĺžky segmentu úrokov:

Rx = √ [(rv)² - h²] = √ [15² - 12²] = √81 = 9

Riešenie e

Miera jedného z diagonálov, napríklad diagonálu, ktorá sa spája s vrcholmi R a T, čo je hlavný diagonálny, je daný kosínovou vetou, ako už bolo vysvetlené, takže nahradzujeme hodnoty tam:

D_M = √ (20² + 25² - 2. dvadsať. pätnásť .Cos 126.87 °) = 37.22 u.do.

Pre menšie diagonálne:

D_m = √ (20² + 25² - 2. dvadsať. pätnásť .Cos 53.13.) = 25.79 u.do.

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Baldor, a. 1973. Geometria a trigonometria. Stredoamerický kultúrny úvodník.
3. A. Do. 2003. Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
4. Jiménez, r. 2010. Matematika II. Geometria a trigonometria. Druhé vydanie. Sála.
5. Pravidelné polygóny. Získané z: kamarát.inžinierstvo.Usac.Edu.Gt.
6. Vesmír. Naháňačka. Získané z: Universoformulas.com.
7. Wikipedia. Naháňačka. Obnovené z: je.Wikipedia.orgán.