Charakteristiky šikmé trojuholníky, príklady, cvičenia

Ten Šikmé trojuholníky Sú to tí, ktorí nemajú žiadny pravý uhol, preto žiadny z ich vnútorných uhlov sa rovná 90 °. Takže šikmý trojuholník môže byť Akulógový alebo tupý.

V prvom prípade sú vnútorné uhly trojuholníka akútne alebo čo je rovnaké: menej ako 90 °, zatiaľ čo v druhom je vždy uhol väčší ako 90 °, to znamená tupý uhol. Pozrime sa na príklad každého z nasledujúcich obrázkov:

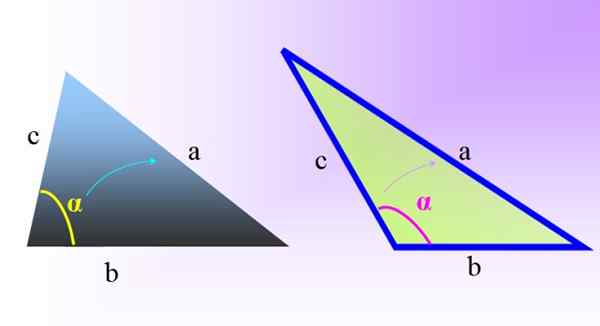postava 1. Šikmé trojuholníky: vľavo šikmý a acutangle trojuholník. Vpravo šikmý a tupý trojuholník. Zdroj: f. Zapata.

Ak chcete nájsť dĺžky bokov a miery vnútorných uhlov tohto druhu trojuholníkov, v neprítomnosti priamych uhlov nie je možné aplikovať vetu Pythagoras.

Existujú však alternatívy na vyriešenie trojuholníka: vety kosínutia a prstenca a skutočnosť, že súčet vnútorných uhlov sa rovná 180 °.

[TOC]

Príklady trojuholníkov oblicuágulos

Vedenie na obrázku 1, môžeme ľahko rozpoznať šikmé trojuholníky prostredníctvom dvoch kritérií, ktoré dáme nižšie.

Trojuholník

Byť trojuholníkom strany A, B a C, s uhlom a uhlom pred bokom.

Ak je štvorec na strane oproti akútnemu uhlu a menší ako súčet štvorcov zvyšných strán, trojuholník je akutangle. Algebraicky:

do² < b² + c²; α < 90º

Relatívny rovnostranný trojuholník, ten, kto má svoje tri strany toho istého opatrenia, je acutangle, a preto šikmý, pretože jeho vnútorné uhly sú rovnaké a merajú 60 °.

Tupý trojuholník

Na druhej strane, ak štvorec na opačnej strane do Pri tupom uhle je väčší ako súčet štvorcov ostatných dvoch, sme v prítomnosti tupého trojuholníka. Preto:

do² > b² + c²; α> 90 °

Napríklad trojuholník, ktorého vnútorné uhly sú 105 °, 60 ° a 15 °, je tupý šikmý trojuholník. Všimnite si, že 105 ° + 60 ° + 15 ° = 180 °.

Vety sínus a kosínus

Na vyriešenie šikmých trojuholníkov, to znamená, že nájdete opatrenia všetkých ich strán a všetkých ich uhlov, sú potrebné vety prsníka a kosínu.

Nechajte A, B a C po stranách trojuholníka a α, β a y ich vnútorné uhly. Tak:

Veta

Veta prsníka stanovuje nasledujúce:

Kde a je opačný uhol od strany A, β je uhol proti bočnej b a y je uhol pred stranou C.

Môže vám slúžiť: Antidevatívne: vzorce a rovnice, príklady, cvičenia

Ekvivalent:

Rozhodli sme sa aplikovať vetu prsníka, keď sa chystáme vyriešiť trojuholník, ako je známe viac uhlov ako strany.

Coseno veta

Podľa Coseno Theorrem:

c² = a² + b² - 2 štúp γ γ

Uhol γ je opäť pred bokom c. Môžeme tiež písať rovnocenné výrazy pre strany A a B takto:

do² = b² + c² - 2 Dobre Bind

A

b² = a² + c² - 2 šložený

Kozínová veta sa aplikuje, ak je hodnota dvoch strán a uhol medzi nimi známy. Akonáhle sú známe tri strany trojuholníka, veta nám umožňuje vypočítať kosínus uhla medzi dvoma z nich.

Vyriešené cvičenia

- Cvičenie 1

Skontrolujte, či je trojuholník, ktorého strany merajú 20, 10 a 12 ľubovoľné jednotky.

Riešenie

Nepoznáme žiadny z vnútorných uhlov, ale podľa kritérií, ktoré slúžia na rozpoznávanie tupých trojuholníkov, môžeme zvýšiť nerovnosti so štvorcami strán, aby sme pozorovali, ak sa splnia.

Najprv nájdeme štvorce na každej strane:

dvadsať² = 400

10² = 100

12² = 144

A to skutočne vidíme: 400> 100 + 144, od 400> 244. Preto trojuholník obsahuje uhol väčší ako 90 °, ktorý sa nachádza pred bokom, ktorý meria 20. V dôsledku toho je tento trojuholník, okrem toho, že je šikmý.

- Cvičenie 2

Vzhľadom na šikmý trojuholník znázornený na obrázku 2, ktorého miery sú uvedené v ľubovoľných jednotkách, určte:

a) Hodnota x. Je to acutangle alebo tupý trojuholník?

b) zostávajúce vnútorné uhly trojuholníka

c) obvod

d) oblasť.

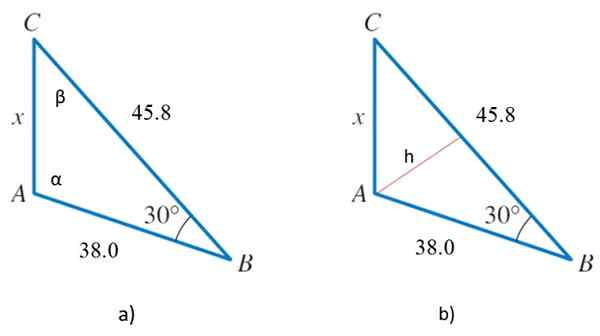Obrázok 2. 2a) trojuholník pre rok vyriešený 2 a 2b) Rovnaký trojuholník s výškou, ktorý bude slúžiť na určenie oblasti. Zdroj: f. Zapata.

Roztok

Z trojuholníka sú známe dve susedné strany, ktorých opatrenia sú 38.0 a 45.8 a uhol medzi nimi, ktorý je 30 °, a preto sa kosínová veta okamžite aplikuje:

X² = 38.0² + Štyri. Päť.8² - 2 x 38.0 x 45.8 x cos 30 ° = 527.18

Preto:

x = (527.18)^1/2 = 22.96

Výkres naznačuje, že a> 90 ° a trojuholník sú okrem šikmej tupej. Aby sme to skontrolovali, zistíme štvorce strán, ako sa to stalo v predchádzajúcom cvičení:

22.96² = 527.18

38.0² = 1444.00

Štyri. Päť.8² = 2097.64

Uhol a je väčší ako 90 °, ak je pravdivý ako štvorec opačnej strany: 45.8²  Je väčší ako súčet štvorcov ostatných strán, čo je 22.96² + 38.0².

Môže vám slúžiť: zákony exponentov

Uvidíme, či sa to stane:

527.18 + 1444.00 = 1971.2

Naozaj:

2097.64> 1971.2

Preto je uhol a je väčší ako 90 °.

Riešenie B

Teraz môžeme aplikovať vetu prsníka, aby sme našli jeden z chýbajúcich uhlov. Budeme to zdvihnúť pre Angle β:

Sen 30 ° / 22.96 = SIN β / 38

Sen β = 38 x (sen 30 ° / 22.96) = 0.8275

β = arcsen (0.8275) = 55.84 °

Chýbajúci uhol je možné nájsť s vedomím, že súčet vnútorných uhlov akéhokoľvek trojuholníka je 180 °. Preto:

55.84 ° + 30 ° + a = 180 °

a = 94.16 °

Ak je uprednostňovaný, môžete tiež použiť kosínusovú vetu na nájdenie kosínusu uhla, ktorý je medzi dvoma susednými stranami. Akonáhle sa funkcia Coseno ARC použije na určenie uhol.

Výsledky sa môžu v desatinných miestach trochu líšiť.

Riešenie c

Obvod P je obrysom obrázku, ktorý je rovnocenný so súčtom opatrení troch strán:

P = 22.96 + 38.00 + 45.80 = 106.76 ľubovoľných jednotiek.

Riešenie d

Vzorec na výpočet plochy každého trojuholníka je:

A = (1/2) x Base X Výška

Potrebujeme zvoliť jednu zo strán ako základňu a určiť výšku. Napríklad výber strany, ktorá meria 45.8, nakreslíme výšku h do vrcholu A, čo je červená čiara na obrázku 2b.

Tým rozdeľujeme pôvodný trojuholník na dva obdĺžniky, obaja s h ako bežné kateto. Každý z nich slúži, pretože poznáme ostrú stranu a uhol.

Vezmeme toho, kto má hypotenusu rovnú 38, kategóriu, ktorá meria h, čo je hľadaná výška a akútny uhol rovný 30 °.

S pomocou trigonometrických dôvodov akútneho uhla 30 ° určujeme hodnotu h:

Sen 30 ° = Cateto oproti 30 ° / hypotenusa = H / 38

H = 38 x sen 30 ° = 19

Preto:

A = (1/2) x 45.8 x 19 = 435.1 svojvoľné oblasti oblasti.

Mohli sme zvoliť inú stranu ako základňu, napríklad stranu 38, v takom prípade výška h Je to iné, pretože sa tvorí ďalší obdĺžnikový trojuholník, ale výsledok oblasti je rovnaký. Pre čitateľa zostáva cvičenie, aby to skontroloval.

- Cvičenie 3

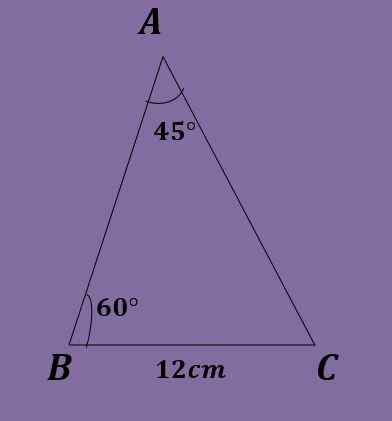
Vzhľadom na trojuholník ABC, že a = 45 °, b = 60 ° a a = 12 cm, vypočítajte ďalšie údaje o trojuholníku.

Môže vám slúžiť: Známky zoskupenia

Riešenie

Pomocou tohto súčtu vnútorných uhlov trojuholníka sa rovná 180 °, musí:

C = 180 °-45 °-60 ° = 75 °.

Tri uhly sú už známe. Potom pokračujeme v použití zákona o prsníku na výpočet dvoch strany, ktoré chýbajú.

Vznikajú rovnice, sú 12 / bez (45 °) = b / bez (60 °) = c / bez (75 °).

Od prvej rovnosti môžete vyčistiť „b“ a získať to:

b = 12*bez (60 °)/bez (45 °) = 6 √6 ≈ 14.696 cm.

Môžete tiež vyčistiť „C“ a získať to:

C = 12*sin (75 °)/sin (45 °) = 6 (1+√3) ≈ 16.392 cm.

- Cvičenie 4

Vzhľadom na trojuholník ABC tak, že a = 60 °, c = 75 ° a b = 10 cm, vypočítajte ďalšie údaje o trojuholníku.

Riešenie

Rovnako ako v predchádzajúcom roku musíte b = 180 °-60 °-75 ° = 45 °. Okrem toho pomocou zákona o prsníku musíte / bez (60 °) = 10 / bez (45 °) = c / bez (75 °), kde sa získa, že a = 10*bez (60 °) / bez (45 °) = 5 √6 ≈ 12.247 cm a c = 10*sin (75 °)/bez (45 °) = 5 (1+√3) ≈ 13.660 cm.

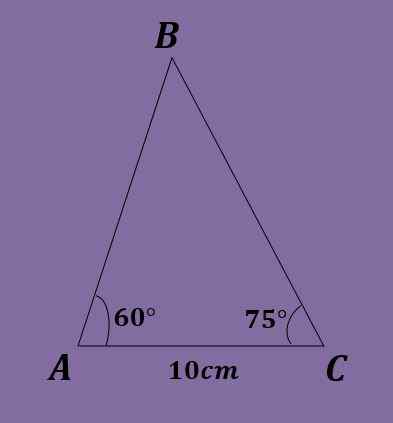
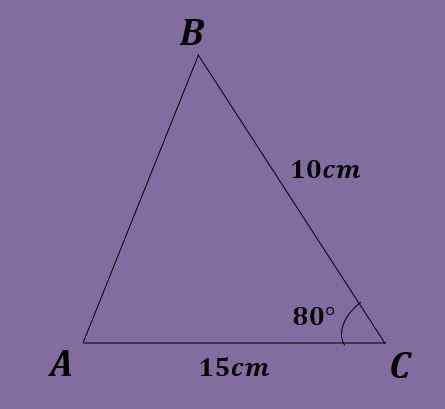
- Cvičenie 5

Vzhľadom na trojuholník ABC tak, že a = 10 cm, b = 15 cm a c = 80 °, vypočítajte ďalšie údaje o trojuholníku.

Riešenie

V tomto cvičení je známy iba uhol, preto nie je možné začať, ako sa to stalo v dvoch predchádzajúcich cvičeniach. Okrem toho nie je možné uplatniť zákon o prsníku, pretože nie je možné vyriešiť žiadnu rovnicu.

Preto sa uplatňuje zákon Cosenos. Musíš:

C² = 10²+15² - 2 (10) (15) cos (80 °) = 325 - 300*0.173 ≈ 272.905 cm,

Takže C ≈ 16.51 cm. Teraz, keď poznáme 3 strany, používa sa zákon o prsníku a získa sa, že:

10 / bez (a) = 15 / bez (b) = 16.51 cm /bez (80 °).

Odtiaľ, keď je číry B bez (b) = 15*bez (80 °)/ 16.51 ≈ 0.894, čo naznačuje, že B ≈ 63.38 °.

Teraz je možné získať, že a = 180 ° - 80 ° - 63.38 ° ≈ 36.62 °.

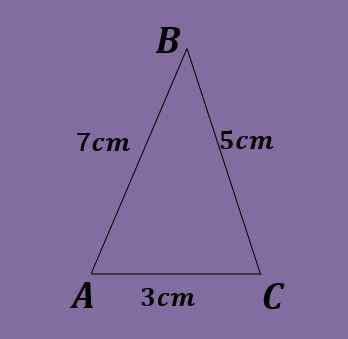
- Cvičenie 6

Strany šikmého trojuholníka sú a = 5 cm, b = 3 cm a c = 7 cm. Vypočítajte uhly trojuholníka.

Riešenie

Zákon o prsníku sa opäť nedá uplatniť priamo, pretože žiadna rovnica by neslúžila na získanie hodnoty uhlov.

Pomocou zákona o kosínus musíte C² = a² + b² - 2ab cos (c), odkiaľ, keď cos (c) = (a² + b² - c²)/ 2ab = (5² + 3² -7²)/ 2*5 *3 = -15/30 = -1/2, a preto C = 120 °.

Teraz je možné uplatniť zákon o prsníku, a tak získať 5/bez (a) = 3/bez (b) = 7/bez (120 °), kde b je možné vyčistiť b a získať ho bez (b) = 3* )/7 = 0.371, takže b = 21.79 °.

Nakoniec sa posledný uhol vypočíta pomocou a = 180 °-130 °-21.79 ° = 38.21.

Odkazy

1. Clemens, s. Geometria s aplikáciami. Addison Wesley.
2. Ibáñez, P. 2010. Matematika III. Učenie sa.
3. Jiménez, r. Matematika II: Geometria a trigonometria. Druhý. Vydanie. Pearson.
4. Matematika pre vás. Tupý trojuholník. Obnovené z: matematiky pre.Slovník.com.
5. Stewart, J. 2007. Predbežné vyfarbenie. 5. Vydanie. Učenie sa.