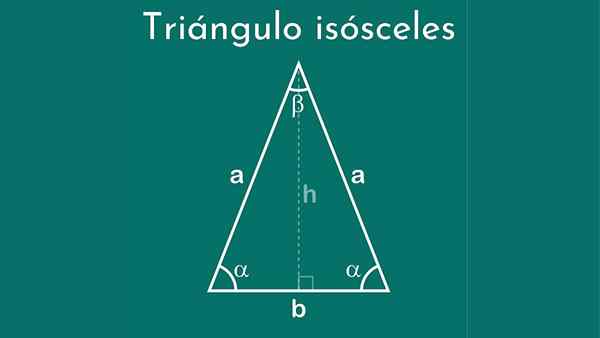
Rovnoramenný trojuholník

Isosceles trojuholník má dve rovnaké strany a jeden iný

Čo je to Isosceles Triangle?

A rovnoramenný trojuholník Je to polygón s tromi zvrhnutím, kde dvaja z nich majú rovnaké opatrenie a tretia strana iná miera. Táto posledná strana sa nazýva základňa. Kvôli tejto charakteristike bolo dané toto meno, čo v gréčtine znamená „rovnaké nohy“.

Trojuholníky sú polygóny považované za najjednoduchšie v geometrii, pretože sú tvorené tromi stranami, tromi uhlami a tromi vrcholmi. Sú to tí, ktorí majú najmenší počet strán a uhlov vzhľadom na ostatné polygóny, ich použitie je však veľmi rozsiahle.

Charakteristiky trojuholníkov Isosceles

Isosceles trojuholník bol klasifikovaný pomocou miery svojich strán ako parametra, pretože dve z jeho strán sú zhodné, to znamená, že majú rovnakú dĺžku.

Podľa amplitúdy vnútorných uhlov sú trojuholníky Isosceles klasifikované ako:

• Isosceles obdĺžnikový trojuholník: Dve z jeho strán sú rovnaké. Jeden z jeho uhlov je rovný (90^ani) A ostatné sú rovnaké (45^ani každý)
• Isosceles tupý trojuholník: Dve z jeho strán sú rovnaké. Jeden z jeho uhlov je tupá (> 90^ani).
• Isosceles acutangle trojuholník: Dve z jeho strán sú rovnaké. Všetky jeho uhly sú akútne (< 90^ani), Kde dvaja majú rovnaké opatrenie.

Komponenty

• Stredný: Je to čiara, ktorá odchádza zo stredu na jednej strane a dosahuje opačný vrchol. Tri médiá sa zúčastňujú v bode zvanom Baricentro alebo Centroid.
• Bisektor: Je to čiastočne, ktorý rozdeľuje uhol každého vrcholu do dvoch uhlov rovnakej miery. Preto je známy ako os symetrie a tento typ trojuholníkov má iba jeden.
• Mediacia: Je to segment kolmo na stranu trojuholníka, ktorý pochádza v strede tohto. V trojuholníku sú tri mediatiky a zúčastnia.
• Výška: Je to čiara, ktorá prechádza z vrcholu na stranu, ktorá je opačná a táto čiara je kolmá na túto stranu. Všetky trojuholníky majú tri výšky, ktoré sa zhodujú v bode nazývanom ortocenter.

Isosceles trojuholníkové vlastnosti

Isosceles trojuholníky sú definované alebo identifikované, pretože majú niekoľko vlastností, ktoré ich zastupujú, pochádzajú z teorémov navrhnutých veľkými matematikmi:

Vnútorné uhly

Súčet vnútorných uhlov sa vždy rovná 180^ani.

Súčet strán

Súčet opatrení dvoch strán by mal byť vždy väčší ako miera tretej strany, a + b> c.

Zhodné strany

Isosceles trojuholníky majú dve strany s rovnakou mierou alebo dĺžkou; to znamená, že sú zhodní a tretia strana sa líši od nich.

Zhodné uhly

Isosceles trojuholníky sú známe aj ako izoangulárne trojuholníky, pretože majú dva uhly, ktoré majú rovnaké opatrenie (zhodné). Sú umiestnené v spodnej časti trojuholníka, na rozdiel od bokov, ktoré majú rovnakú dĺžku.

Môže vám slúžiť: lichobežník

Z tohto dôvodu veta, ktorá to ustanovuje:

„Ak má trojuholník dve zhodné strany, uhly na rozdiel od týchto strán budú tiež zhodné“. Preto, ak je trojuholník izosceles, uhly jeho základní sú zhodné.

Príklad:

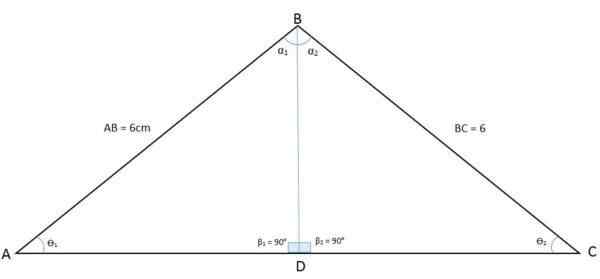
Na nasledujúcom obrázku je pozorovaný trojuholník ABC. Pri kreslení svojho rozdelenia z vrcholu uhla B k základni je trojuholník rozdelený na dva trojuholníky BDA a BDC:

Bisektor, ktorý sa delí na dva trojuholníky rovnajúce sa trojuholníkovi Isosceles

Týmto spôsobom bol uhol vrcholu B tiež rozdelený do dvoch rovnakých uhlov. Bisektor je teraz spoločnou stranou (BD) medzi týmito dvoma novými trojuholníkmi, zatiaľ čo strany AB a BC sú zhodné strany. Toto je prípad strany, uhol, strany (LAL).

To ukazuje, že uhly vrcholov A a C majú rovnaké opatrenie, ako aj je možné preukázať, že keďže trojuholníky BDA a BDC sú zhodné, strany AD a DC sú tiež.

Výška, medián, mediatrix a bisektor sú náhodné

Čiara nakreslená od vrcholu oproti základne k stredu základne trojuholníka Isosceles je súčasne výška, medián a mediatrix, ako aj bisektor vzhľadom na opačný uhol základne.

Všetky tieto segmenty sa zhodujú v jednom, ktorý ich predstavuje.

Príklad:

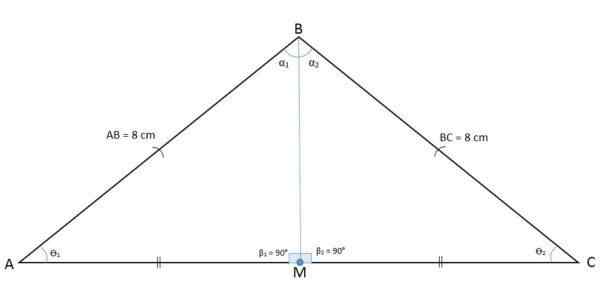
Na nasledujúcom obrázku je trojuholník ABC pozorovaný so stredným bodom, ktorý rozdeľuje základňu na dva segmenty BM a CM.

Výška, medián, mediatrix a bisektor sú náhodné

Pri kreslení segmentu z bodu M do opačného vrcholu sa podľa definície získa medián AM, ktorý je relatívne k vrcholu A a na strane BC.

Pretože segment AM rozdeľuje trojuholník ABC na dva rovnaké trojuholníky Amc a Amc, znamená to, že prípad bokov, uhol, strany, a preto AM bude tiež bisektorom Bâc.

Preto sa Bisector bude vždy rovnať mediánu a naopak.

Segment AM tvorí uhly, ktoré majú rovnaké opatrenie pre trojuholníky AMC a AMC; to znamená, že sú doplnkové, takže miera každého bude:

Prezerať. (Amb) + Med. (AMC) = 180^ani

2 _* Prezerať. (AMC) = 180^ani

Prezerať. (AMC) = 180^ani ÷ 2

Prezerať. (AMC) = 90^ani

Je známe, že uhly tvorené segmentom AM, pokiaľ ide o základňu trojuholníka, sú rovné, čo naznačuje, že tento segment je úplne kolmý na základňu.

Preto predstavuje výšku a mediatriu, s vedomím, že m je stredný bod.

Preto riadok AM:

• Predstavuje výšku BC.
• Je stredná veľkosť.
• Je obsiahnutý v mediatrici BC.
• Je to bisektor vrcholového uhla â

Relatívna výška

Výšky, ktoré sú relatívne k rovnakým stranám, majú rovnaké opatrenie tiež.

Môže vám slúžiť: perfektné čísla: Ako ich identifikovať a príklady

Pretože Isosceles Triangle má dve rovnaké strany, jeho dve príslušné výšky budú tiež rovnaké.

Orocentro, Baricentro, Incentro a Colecentro Coinsides

Keďže výška, medián, bisektor a mediatrix súvisiaca so základňou sú súčasne zastúpené rovnakým segmentom, ortocenter, baricentro, snidnica a obvody budú kolineálne body, to znamená, že sa nachádzajú v rovnakej línii:

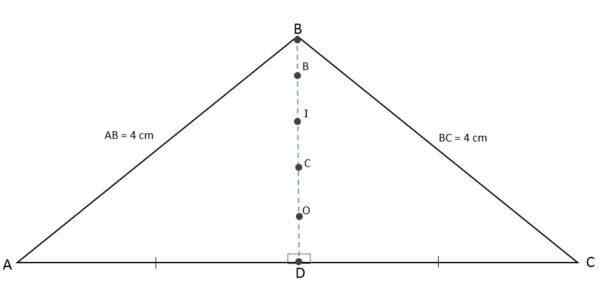Ortocenter, Baricentro, Incentro a CirundCentro sú tiež náhodné

Výpočet trojuholníkov Isosceles

Ako vypočítať obvod?

Obvod polygónu sa vypočíta na základe súčtu strán.

Rovnako ako v tomto prípade má trojuholník Isosceles dve strany s rovnakým opatrením, jeho obvod sa počíta s nasledujúcim vzorcom:

P = 2_*(strana A) + (strana b).

Ako vypočítať výšku?

Výška je čiara kolmá na základň.

Výška predstavuje opačný kateto (a), polovicu základne (b/2) k susednému kateto a strana „A“ predstavuje hypotenus.

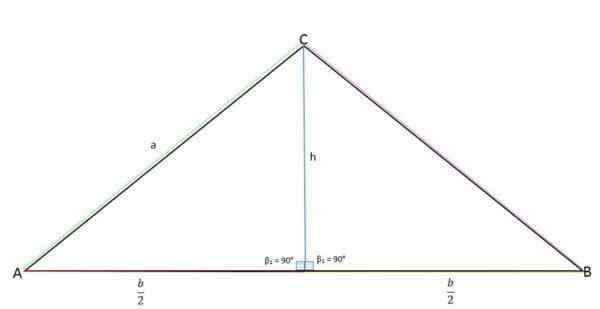Výpočet výšky trojuholníka Isosceles

Pomocou vety Pythagora je možné určiť hodnotu výšky:

do² + b² = c²

Kde:

do² = výška (h).

b² = B / 2.

c² = strana a.

Nahradenie týchto hodnôt vo vete Pythagoras a vyčistenie výšky, ktorú máte:

h² + (b / 2)² = do²

h² + b² / 4 = do²

h² = do² - b² / 4

H = √ (do² - b² / 4).

Ak je uhol tvorený zhodnými stranami, výška je možné vypočítať pomocou nasledujúceho vzorca:

Ako vypočítať oblasť?

Trojuholníky sa vždy vypočítavajú s rovnakým vzorcom, ktorý vynásobí základňu podľa výšky a vydelí sa 2:

Existujú prípady, keď sú známe iba opatrenia na dvoch stranách trojuholníka a uhol, ktorý sa medzi nimi vytvára. V takom prípade je potrebné určiť oblasť, je potrebné uplatniť trigonometrické dôvody:

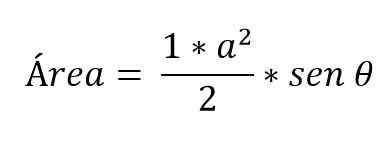
Ako vypočítať základňu trojuholníka?

Pretože Isosceles Triangle má dve rovnaké strany, na určenie hodnoty svojej základne je potrebné poznať aspoň mieru výšky alebo jedného z jej uhlov.

Poznanie výšky sa používa veta Pythagoras:

do² + b² = c²

Kde:

do² = výška (h).

c² = strana a.

b² = B / 2, nie je známe.

Vyčistíme b² vzorca a musíme:

b² = a² - c²

B = √ a² - c²

Pretože táto hodnota zodpovedá polovici základne, musí sa vynásobiť 2, aby sa získala úplná miera základne trojuholníka izoscelov:

B = 2 _* (√ a² - c²)

V prípade, že je známa iba hodnota jej rovnakých strán a uhol medzi nimi, aplikuje sa trigonometria a vytiahne čiaru od vrcholu k základni, ktorá rozdeľuje trojuholník Isosceles na dva obdĺžnikové trojuholníky.

Týmto spôsobom sa polovica základne počíta s:

Hodnota výšky a uhla vrcholu, ktorý je proti základni, je tiež známa. V takom prípade je možné určiť základňu trigonometrie:

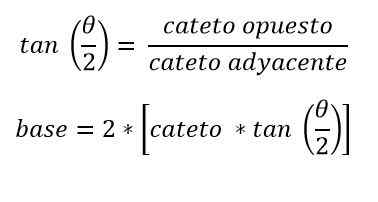
Cvičenia

Prvé cvičenie

Nájdite oblasť Isosceles ABC Triangle, s vedomím, že dve z jeho strán merajú 10 cm a tretia strana meria 12 cm.

Môže vám slúžiť: Antidevatívne: vzorce a rovnice, príklady, cvičenia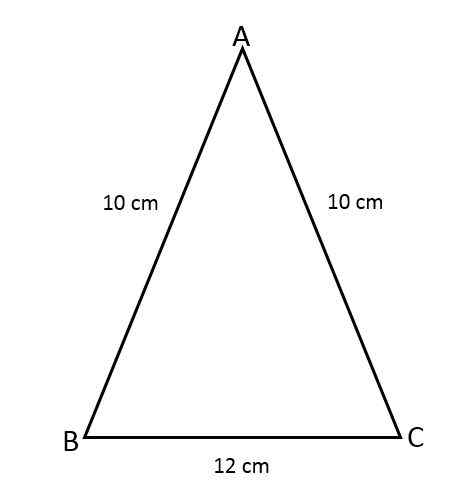

Riešenie

Ak chcete nájsť oblasť trojuholníka, je to potrebné.

K dispozícii sú nasledujúce údaje o trojuholníku Isosceles:

• Rovnaké strany (a) = 10 cm.
• Báza (b) = 12 cm.

Hodnoty sa nahradia vo vzorci:

Druhé cvičenie

Dĺžka dvoch rovnakých strán iSosceles trojuholníka Meria 42 cm, spojenie týchto strán tvorí uhol 130^ani. Stanovte hodnotu tretej strany, plocha tohto trojuholníka a obvodu.

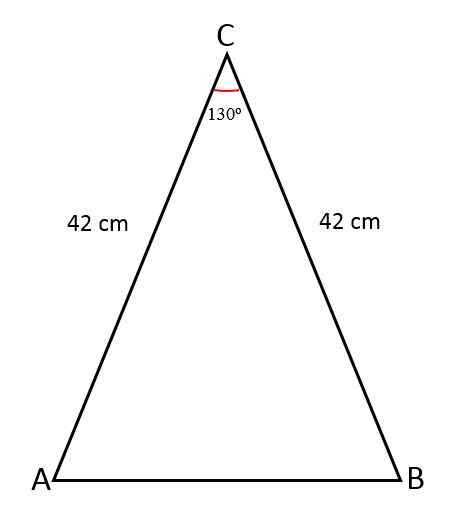
Riešenie

V tomto prípade sú medzi nimi známe miery bokov a uhol.

Ak chcete poznať hodnotu chýbajúcej strany, to znamená základňu tohto trojuholníka, je na ňu čiara kolmá na ňu, ktorá rozdelí uhol do dvoch rovnakých častí, jedna pre každý vytvorený trojuholník obdĺžnika.

• Rovnaké strany (a) = 42 cm.
• Uhol (ɵ) = 130^ani

Teraz, trigonometriou, sa vypočíta hodnota polovice bázy, ktorá zodpovedá polovici hypotenusu:

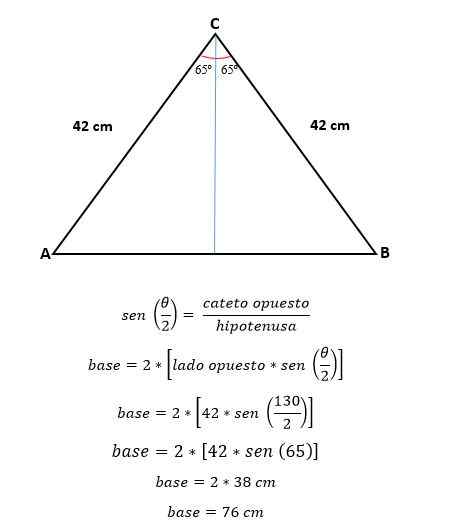
Na výpočet oblasti je potrebné poznať výšku tohto trojuholníka, ktorý sa dá vypočítať pomocou trigonometrie alebo vety Pythagorov, teraz, keď už bola hodnota základne stanovená.

Trigonometriou bude:

Perimeter sa vypočíta:

P = 2_*(strana A) + (strana b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Tretie cvičenie

Vypočítajte vnútorné uhly trojuholníka Isosceles, s vedomím, že základný uhol je â = 55^ani

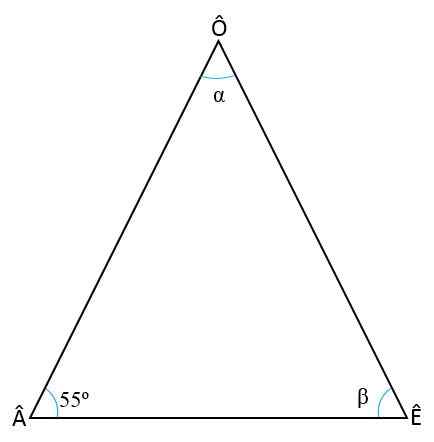
Riešenie

Ak chcete nájsť dva chýbajúce uhly (ê a ô), je potrebné si zapamätať dve vlastnosti trojuholníkov:

• Súčet vnútorných uhlov každého trojuholníka bude vždy = 180^ani:

 + ê + ô = 180 ^ani

• V iSosceles trojuholníku sú uhly základne vždy zhodné, to znamená, že majú rovnaké opatrenie, preto:

= Ô

Ê = 55^ani

Na určenie hodnoty uhla ê sa vymenia hodnoty ostatných uhlov v prvom pravidle a vyčistia sa ê:

55^ani + 55^ani + Ô = 180 ^ani

110 ^ani + Ô = 180 ^ani

Ô = 180 ^ani - 110 ^ani

Ô = 70 ^ani.

Odkazy

1. Álvarez, e. (2003). Elementy geometrie: s mnohými cvičeniami a geometriou kompasu. University of Medellin.
2. Álvaro Rendón, do. R. (2004). Technická kresba: Notebook aktivity.
3. Anjel, a. R. (2007). Elementárna algebra. Pearson Vzdelanie.
4. Arthur Goodman, L. H. (Devätnásť deväťdesiat šiestich). Algebra a trigonometria s analytickou geometriou. Pearson Vzdelanie.
5. Baldor, a. (1941). Algebra. Havana: kultúra.
6. José Jiménez, L. J. (2006). Matematika 2.
7. Tuma, j. (1998). Inžinierska matematika. Wolfram Mathworld.