Úvodník

postava 1.- Vľavo pravidelný Tridecácágone a napravo mena 20 korún Českej republiky, s obrysom v tvare Bridecagon, ktorý je v obvode napísaný v obvode, na jednej strane má lev Čiemi a na druhej Českej republiky, namontovaná na koni. Zdroj: f. Zapata.

Čo je Tridecágono?

Tridecagon je plochá geometrická postava rodiny polygónov a ktorá sa vyznačuje tým, že má 13 strán a 13 vrcholov. Ďalším názvom tohto polygónu je Triskaidecágono, Číslo odvodené z gréčtiny.

13 strán sú segmenty čiary, ktoré sa konečne blízko formujú obrázku. Polygóny, ktoré sú pomenované podľa množstva strán, sú bohatým zdrojom inšpirácie pre architektúru, konštrukciu a dizajn mnohých predmetov, umenia aj utilitariánov.

Vlastnosti Tridecágono

Tridecágono zdieľa s ostatnými polygónmi nasledujúce charakteristiky a vlastnosti:

-Strany, Sú to segmenty čiary, ktoré sú spojené s vytvorením čísla, ktoré je v prípade Tridecágona 13. Sú identifikované malými písmenami.

-Vrcholy, To sa nazývajú križovatky po sebe idúcich strán a zvyčajne označujú kapitálové listy. Tridecágono má 13 vrcholov.

-Obvod, rovnocenné so súčtom bokov. Ak majú všetky strany rovnakú mieru „a“, obvod je jednoducho 13 × a, ale ak sú strany nerovnaké, obvod pridá každú zo dĺžok strán strany.

-Stred, Je to bod, ktorý udržiava rovnakú vzdialenosť s vrcholmi aj bokmi.

-Diagonálny, Čiara, ktorá sa pripojí k vrcholu k inému nekonečnému vrcholu (po sebe idúce vrcholy sú spojené zo strany).

-Vnútorné uhly, Vytvárajú sa medzi dvoma susednými stranami postavy a na vnútornej časti polygónu a jeho vrchol je spoločným vrcholom na oboch stranách.

Môže vám slúžiť: Miletus takúto vetu

-Vonkajšie uhly, Sú mimo polygónu, medzi jednou stranou a predĺžením jednej z po sebe idúcich strán do prvej.

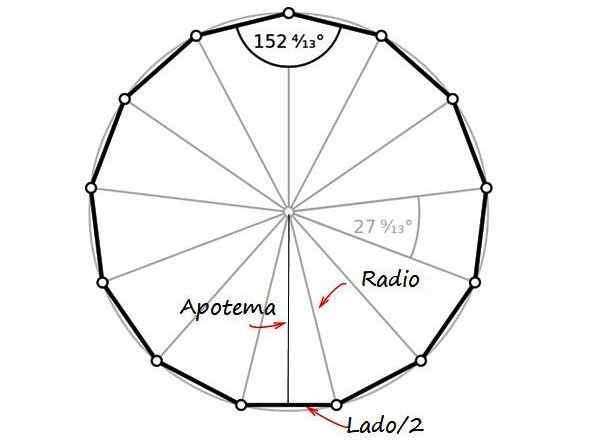
-Rozhlas, Vzdialenosť-Vertix Tridecágonu.

-Centrálny uhol, Je to ten, ktorého vrchol je stred polygónu.

-Apotém, segment, ktorý sa spája do stredu jednej strany so stredom obrázku a tvorí 90 ° s touto stranou.

Pravidelný a nepravidelný hromy

Threecarons môže byť:

-Pravidelný, Keď je miera všetkých jeho trinástich strán rovnaká a jeho vnútorné uhly zmerajú rovnaké.

-Nepravidelný, Ak má jedna alebo viac strán rôzne opatrenia.

V prípade pravidelného Tridecacágone je možné uplatniť tieto vzorce:

Vnútorný

V prípade pravidelného polygónu je vzorec, ktorý umožňuje vypočítať hodnotu vnútorného uhla:

Kde n predstavuje počet strán, čo je v tomto prípade 13. S touto hodnotou to je:

I = (11 × 180 °)/13 ≈ 152.Tretí

Diagonála

Počet diagonalov sa vypočíta podľa nasledujúceho vzorca, dokonca platný, ak je polygón nepravidelný:

Pre n = 13 výsledkov:

D = 13 × 10/2 = 65 diagonálov

Apotém

Hodnota apotheme l_Do  Vypočíta sa s nasledujúcim vzorec, ktorý je „A“ dĺžkou strany:

L_Do ≅ 2.0286A

Oblasť

Ak obvod P a dĺžka apotémie l_Do, Oblasť Tridecágono sa počíta:

A = (p × l_Do)/2

V závislosti od strany „A“ zostáva vzorec:

A = (13a × l_Do)/2

Výmena opatrenia_Do Z predchádzajúcej časti sa získa vzorec pre oblasť, ktorá závisí iba od dĺžky strany:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Môže vám slúžiť: Hypergeometrické rozdelenie: vzorce, rovnice, model

Cvičenie

Ak je priemer korún 20 mm 26 mm, koľko sú bočné a plocha Tridecágono zaregistrované v kruhu meny?

Riešenie

Z obrázku je obdĺžnikový trojuholník, ktorého kategórie sú apothémia a polovica dĺžky strany, pričom hypotenusa sa rovná polomeru meny, čo je polovica priemeru. Pretože to má hodnotu 26 mm, rádio R sa rovná 13 mm.

Obrázok 2. Rádio, apotheme a polovica strany trindecagonu tvoria obdĺžnikový trojuholník. Zdroj: Wikimedia Commons/F. Zapata.

Autor: Pythagoras Theorrem:

Pretože l_Do ≈ 2.0286A, máte:

R² = (2.0286a)² + (0.5.)² = 4.3652a²

Strana je:

S touto hodnotou je oblasť meny:

A ≈ 13.186a² = 13.186 (6.222 mm)² = 510.5 mm²

Čitateľ je ponechaný na porovnanie tohto výsledku s plochou získanou za predpokladu, že mena je kruhový polomer r = 13 mm.

Ako je na tom Tridecágono?

Pravidelný trindacegón je z polygónov, ktoré nepripúšťajú presnú konštrukciu pomocou pravidla a kompasu, to znamená, že to nie je zostavený polygón. Sú zostaviteľné iba teoreticky, tie polygóny, ktorých počet strán obsahuje iba hlavné faktory formy:

Týmto spôsobom sa nazývajú prvotné čísla Bratranci, Ale číslo 13, hoci je to bratranec, nemá tento formulár.

Môžete však nakresliť pravidelný trindecagón, ktorý je zaregistrovaný v obvode, každý vrchol má križovatku s ním bez toho, aby sa všimol voľným okom. Za to je potrebné.

Môže vám slúžiť: obtusangle trojuholník

Jedným zo spôsobov, ako vybudovať pravidelný Tridecacágone, aj keď nie jediný, je kreslenie ťahov, ako je uvedené v nasledujúcej animácii:

Obrázok 3. Výstavba pravidelného tridecagonu. Zdroj: Wikimedia Commons.

A táto ďalšia animácia tiež popisuje, ako vyrobiť Tridecágono približne s pravidlom a kompasom:

Obrázok 4.- Alternatívny spôsob, ako vybudovať približne pravidelný tridecagon s pravidlom a kompasom. Zdroj: Wikimedia Commons.

Príklady Tridecagel

Konkávny a konvexný hromy

Keď sú vnútorné uhly Tridecágonu menšie ako 180 °, číslo je konvexné, zatiaľ čo ak je jeden alebo viac vnútorných uhlov väčší ako 180 °, potom je Tridecágono konkávny.

Pravidelný Tridecacán je konvexný, pretože jeho vnútorné uhly merajú približne 152.Tretí každý.

Použitie Tridecágono v numizmatike

Česká koruna

Numizmatics je veda o mincí, medailách, lístkoch a hranolkách. Polygóny na mnohých stranách sú ideálne ako dekoratívne prvky pri návrhu mincí, najmä tie, ktoré majú mnoho strán, ako napríklad Tridecágono.

Nie všetky mince sú okrúhle, polygóny na mnohých stranách sa však podobajú kruhovému tvaru, tým viac strán má, tým väčší prístup. Preto dizajnéri mincí používajú polygóny na mnohých stranách, aby v ich dizajne zaviedli nádych originality.

S týmto účelom sa používajú rôzne polygóny, ako napríklad Horná mena, nazývaná koruna a z Českej republiky, dobrý príklad použitia Tridecágona ako dizajnérskeho prvku.

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Kresba. Pravidelné polygóny. Obnovené z: kresby.com.
3. Hartley, m. Konštrukcia tridecagonu. Obnovené z: YouTube.com
4. Wikipedia. Stavané polygón. Obnovené z: je.Wikipedia.orgán.
5. Wikiwand. Úvodník. Získané z: Wikiwand.com.