Charakteristiky fyzickej trajektórie, typy, príklady a cvičenia

Ten Trajektória vo fyzike Je to krivka, ktorá opisuje mobil pri prechádzaní následnými bodmi počas jeho pohybu. Pretože to môže prijať nespočetné varianty, budú to tiež trajektórie, ktoré môže mobil nasledovať.

Aby sme prešli z jedného miesta na druhé, človek sa môže vydať na rôzne cesty a rôzne spôsoby: pešo cez chodníky v uliciach a uličkách alebo prichádzať autom alebo motocyklom na diaľnicu. Počas jazdy lesom môže chodec sledovať komplikovanú trajektóriu, ktorá zahŕňa zákruty, lezenie alebo vypadávanie a kým neprejde niekoľkokrát cez rovnaký bod.

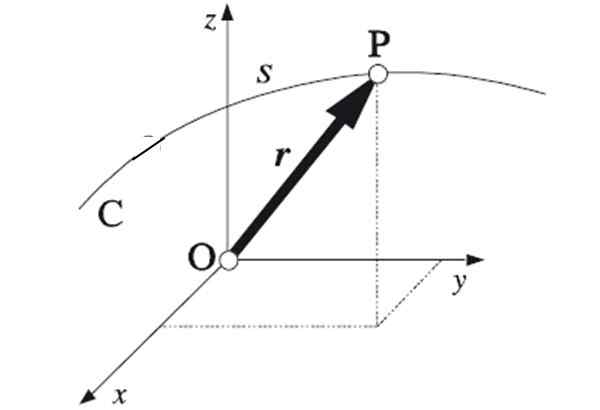postava 1. Spojenie extrémnych bodov každého vektora polohy sa získa trajektória nasledovaná časticou. Zdroj: Algarabia [verejná doména]

Ak body, cez ktoré mobil cestuje, nasledujú priamu čiaru, trajektória bude napätá. Toto je najjednoduchšia trajektória za to, že je jednou dimenziou. Zadanie pozície vyžaduje jednu súradnicu.

Ale mobil môže nasledovať po trajektórii Curvyl, ktorý je možné zatvoriť alebo otvoriť. V týchto prípadoch monitorovanie polohy vyžaduje dve alebo tri súradnice. Toto sú pohyby v rovine a priestore. To sa týka odkazy: Obmedzujúce materiálne podmienky pohybu. Niektoré príklady sú:

- Orbity, ktoré opisujú planéty okolo slnka, sú zatvorené trajektórie tvare elipsy. Aj keď v niektorých prípadoch môžu priblížiť obežník, ako v prípade Zeme.

- Lopta, ktorú brankár kopne do bránkového kopu, sleduje parabolickú trajektóriu.

- Vták v lete popisuje zakrivené trajektórie vo vesmíre, pretože okrem toho, že sa pohybuje v lietadle.

Trajektória fyziky sa dá matematicky vyjadriť, keď je mobilná pozícia známa kedykoľvek v čase. Byť r Polohový vektor, ktorý má zase súradnice X, a a z V najbežnejšom prípade trojrozmerného pohybu. Poznanie funkcie r (T) Trajektória bude úplne určená.

[TOC]

Chlapci

Všeobecne povedané, trajektória môže byť dosť komplikovanou krivkou, najmä ak chcete matematicky vyjadriť. Preto začína najjednoduchšími modelmi, v ktorých mobily cestujú po priamke alebo v lietadle, ktoré môžu byť podlahou alebo iným vhodným:

Pohyby v jednej, dve a tri rozmery

Najštudované trajektórie sú:

- Priamy, Pri cestovaní po vodorovnej, zvislej alebo naklonenej čiare. Lopta vyhodená zvisle nahor nahor túto trajektóriu alebo predmet, ktorý tiež skĺzne z kopca sklonenou rovinou. Sú to jednotlivé pohyby, stačí jediná súradnica na úplné určenie jej polohy.

- Parabolický, v ktorom mobil popisuje oblúk paraboly. Je to časté, pretože akýkoľvek objekt, ktorý sa začal šikmo pod konaním gravitácie (projektil), sleduje túto trajektóriu. Ak chcete zadať mobilnú polohu, musíte dať dve súradnice: X a a.

- Kruhový, sa vyskytuje, keď sa pohybujúca častica riadi obvodom. Je to tiež bežné v povahe a každodennej praxi. Mnoho každodenných predmetov sleduje kruhovú trajektóriu, ako sú pneumatiky, kúsky strojov a satelitov na obežnej dráhe, aby uvádzali niekoľko príkladov.

Môže vám slúžiť: Equocent Vektory: Definícia, notácia, cvičenia

- Eliptický, Objekt sa pohybuje po elipse. Ako sa uvádza na začiatku, je to trajektória, ktorú planéty sledujú na obežnej dráhe okolo slnka.

- Hyperbolický, Astronomické objekty pod pôsobením centrálnej sily (gravitácia) môžu sledovať eliptické (uzavreté) alebo hyperbolické (otvorené) trajektórie, ktoré sú menej časté ako prvé.

- Špirálovitý, o Hnutie špirály, podobne ako v prípade vtáka, ktorý stúpa v tepelnom prúde.

- Hýbať sa, Mobil popisuje oblúk v pohybe spiatočných výletov.

Príklady

Trajektórie opísané v predchádzajúcej časti sú veľmi užitočné na rýchle získanie predstavy o tom, ako sú pohyby objektu. V každom prípade je potrebné objasniť, že trajektória mobilu závisí od umiestnenia pozorovateľa. To znamená, že rovnakú udalosť je možné vidieť rôznymi spôsobmi, podľa toho, kde je každý z nich.

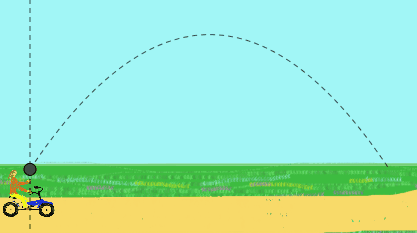
Napríklad dievčenský pedál konštantnou rýchlosťou a vyhodí loptu hore. Poznamenáva, že lopta popisuje rektilineárnu trajektóriu. 

Avšak pre pozorovateľa stojaceho na ceste, ktorá ju vidí, bude mať lopta parabolický pohyb. Pre neho bola lopta spočiatku hodená sklonenou rýchlosťou, výsledok rýchlosti ruky dievčaťa plus rýchlosť bicykla.

Obrázok 2. Táto animácia ukazuje vertikálne spustenie lopty od dievčaťa, ktoré prechádza bicyklom, ako vidí (priama trajektória) a ako vidíte pozorovateľa (parabolická trajektória). (Pripravený f. Zapata).

Trajektória mobilu explicitným, implicitným a parametrickým spôsobom

- Výslovný, Priamo špecifikovanie krivky alebo geometrického miesta dané rovnicou a (x)

- Implicitný, v ktorej je krivka vyjadrená ako f (x, y, z) = 0

-Parametrický, Týmto spôsobom sa súradnice X a Y Z vyskytujú v závislosti od parametra, ktorý je vo všeobecnosti vybraný ako čas tón. V tomto prípade trajektória pozostáva z funkcií: x (t), a (t) a z (t).

Ďalej sú v kinematike podrobne opísané dve veľmi študované trajektórie: parabolická trajektória a obežná trajektória.

Spustenie vo vákuu

Objekt (projektil) sa vyhodí a vytvára uhol A s horizontálnou a počiatočnou rýchlosťou vložka_ani Ako ukazuje obrázok. Vzduchový odpor sa nezohľadňuje. Pohyb sa dá považovať za dva nezávislé a súčasné pohyby: jeden vodorovný s konštantnou a druhou vertikálnou rýchlosťou pod pôsobením gravitácie.

x (t) = x_ani +vložka_vôl.tón

a (t) = y_ani +vložka_Odvoz.T -½g.tón²

Tieto rovnice sú parametrické rovnice spustenia projektilu. Ako je uvedené vyššie, majú spoločný parameter tón, Aký je čas.

V pravom trojuholníku obrázku je možné vidieť:

vložka_vôl = v_ani cos θ_Jo

vložka_Odvoz = v_ani hriech_Jo

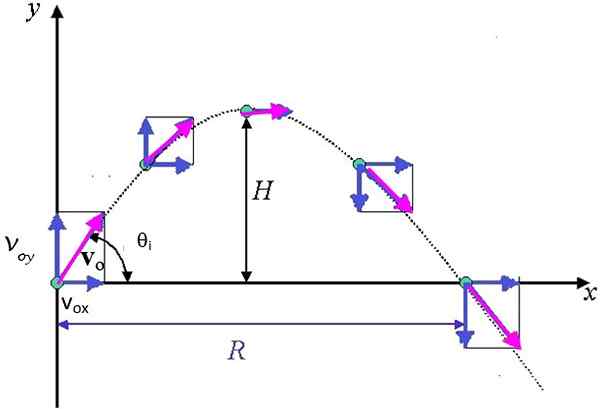Obrázok 3. Parabolická trajektória, po ktorej nasleduje projektil, ktorý ukazuje komponenty vektora rýchlosti. H je maximálna a výška R je maximálny horizontálny dosah. Zdroj: Ayush12gupta [CC BY-SA 4.0 (https: // creativeCommons.Org/licencie/By-SA/4.0)]

Nahradením týchto rovníc, ktoré obsahujú uhol spustenia v parametrických rovniciach, je to:

Môže vám slúžiť: Difrakcia zvuku: Čo je, príklady, aplikácie

x (t) = x_ani +vložka_ani cos θ_Jo.tón

a (t) = y_ani +vložka_ani. hriech_Jo.T -½g.tón²

Rovnica parabolickej trajektórie

Explicitná rovnica trajektórie je vyčistenie t rovnice pre x (t) a nahradenie v rovnici y (t) (t). Na uľahčenie algebraickej práce sa dá predpokladať, že pôvod (0,0) je v mieste štartu a týmto spôsobom x_ani = y_ani = 0.

Po zjednodušení parametra “tón„Bola eliminovaná a rovnica, ktorá zostáva, je a v závislosti od x: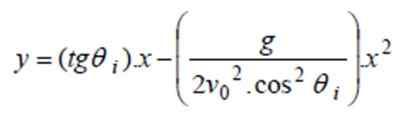

Toto je trajektória rovnica v Výslovný formulár.

Kruhová trajektória

Kruhová trajektória je daná:

(X - x_ani)² + (a - a_ani)² = R²

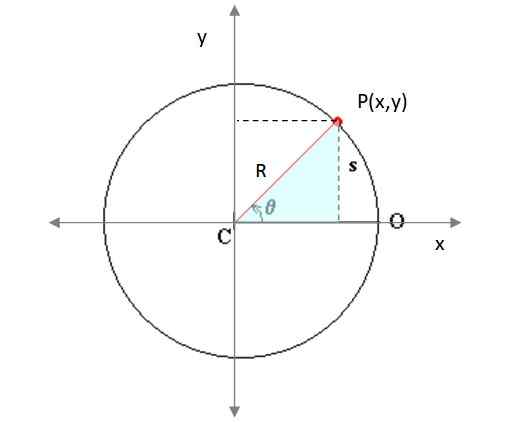Obrázok 4. Častica sa pohybuje v kruhovej trajektórii v rovine. Zdroj: upravené podľa f. Wikimedia Commons Shoe.

Tu x_ani a a a_ani Predstavujú stred obvodu opísaného mobilom a R je polomer toho istého. P (x, y) je bod trajektórie. Z tieňovaného trojuholníka obdĺžnika (obrázok 3) je varované, že:

x = r. cos θ

y = r. hriech

Parameter v tomto prípade je uhol zametania 9, nazývaný uhlové posunutie. V konkrétnom prípade, že uhlová rýchlosť Ω (uhol zametaný na jednotku času) je konštantná, možno potvrdiť, že:

9 = 9_ani + Ωtón

Kde 9_ani Je to počiatočná uhlová poloha častice, ktorá sa bude brať ako 0, redukuje sa na:

9 = Ωtón

V tomto prípade sa čas vráti k parametrickým rovniciam, ako napríklad:

x = r.cos Ωtón

y = r. hriech Ωtón

Jednotkové vektory Jo a J Sú veľmi vhodné napísať funkciu polohy objektu r (T). Označujú pokyny na osi X A na osi a respektíve. Z hľadiska polohy častice, ktorá opisuje rovnomerný kruhový pohyb, je:

r (t) = r.cos Ωtón Jo + R. hriech Ωtón J

Vyriešené cvičenia

Cvičenie vyriešené 1

Kanón môže strieľať guľku s rýchlosťou 200 m/s a uhlom 40 ° vzhľadom na horizontálnu. Ak sa spustenie uskutoční v plochom teréne a odpor vzduchu je opovrhovaný, nájdite:

a) Trajektická rovnica a (x) ..

b) parametrické rovnice x (t) a a (t).

c) Horizontálny dosah a čas, keď projektil vydrží vo vzduchu.

d) výška, v ktorej sa projektil umiestni, keď x = 12.000 m

Riešenie do)

a) Na nájdenie trajektórie sa nahradia hodnoty uvedené v rovnici y (x) predchádzajúcej časti:

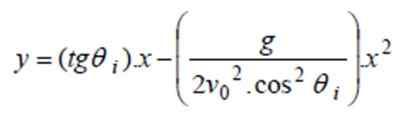
a (x) = tg 40 °. X - 9.8/(2 '400². cos²40 °) X² ⇒  a (x) = 0.8391 x - 0.0000522x²

Riešenie b)

b) Začiatok bodu je vybraný na začiatku súradníckeho systému (0,0):

x (t) = x_ani +vložka_vôl.T = 400'Cos 40 °.T = 306.42. tón.

a (t) = y_ani +vložka_Odvoz.T -½g.tón²= 400 'Sen 40 °.T - 0.5 '9.8't²= 257.12 t - 4.9.tón²

Riešenie c)

c) nájsť čas, ktorý projektil vydrží vo vzduchu, je hotový a (t) = 0, Byť spustením sa uskutoční v plochom teréne:

Môže vám slúžiť: čo je relatívna a absolútna drsnosť?

0 = 257.12.T - 4.9.tón²

T = 257.12/4.9 s = 52.473 s

Horizontálny maximálny rozsah nahrádza túto hodnotu v x (t):

X_Maximálny = 306.4252.47 m = 16077.7 m

Ďalší spôsob, ako nájsť x_Maximálny Priamo robí y = 0 v rovnici trajektórie:

0 = 0.8391 x_Maximálny - 0.0000522 x²_Maximálny

x = 0.8391 /0.0000522 m = 16078.5 m

V dôsledku zaokrúhľovania desatinných miest je malý rozdiel.

D) Riešenie

d) poznať výšku, keď sa x = 12000 m Táto hodnota sa nahradí priamo v rovnici trajektórie:

a (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Cvičenie vyriešené 2

Funkcia polohy objektu je daná:

r (t) = 3t Jo + (4 -5T²) J m

Nájsť:

a) Rovnica pre trajektóriu. Aká je krivka?

b) počiatočná poloha a poloha, keď t = 2 s.

c) posun uskutočnený po t = 2 s.

Riešenie

a) funkcia polohy bola uvedená z hľadiska jednotkových vektorov Jo a J, ktoré určujú adresu na osiach X a a, preto:

x (t) = 3t

a (t) = 4 -5T²

Trajektická rovnica a (x) Vyčistí tón z x (t) a nahradenie a (t):

T = x/3

a (x) = 4 -5. (x/3)² = 4 - 5x²/9 (podobenstvo)

b) Počiatočná poloha je: r (2) = 4 J m ; Pozícia v T = 2 s je r (2) = 6 Jo -16 J m

c) posun Dr Je to odčítanie dvoch polohových vektorov:

Δr = r (2) - r (2) = 6 Jo -16 J- 4 J = 6 Jo - dvadsať J m

Cvičenie vyriešené 3

Zem má polomer r = 6300 km a je známe, že obdobie rotácie jeho pohybu okolo jeho osi je jeden deň. Nájsť:

a) Rovnica trajektórie bodu na zemskom povrchu a jeho funkcia polohy.

b) rýchlosť a zrýchlenie uvedeného bodu.

Riešenie do)

a) funkcia polohy pre akýkoľvek bod na kruhovej obežnej dráhe je:

r (t) = r.cos Ωtón Jo + R.hriech Ωtón J

Máte polomer Zeme r, ale nie uhlovú rýchlosť Ω, ale dá sa vypočítať z obdobia, pretože vie, že pre kruhový pohyb je platné povedať, že:

Ω = 2π × Frekvencia = 2π / obdobie

Obdobie pohybu je: 1 deň = 24 hodín = 1440 minút = 86400 sekúnd, preto:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Výmena vo funkcii polohy:

r (t) = r.cos Ωtón Jo + R. hriech Ωtón J = 6300 (cos 0.000023148T Jo + hriech 0.000023148T J) Km

Cesta v parametrickom formulári je:

x (t) = 6300. cos 0.000023148T

a (t) = 6300. hriech 0.000023148T

Riešenie b)

b) pre kruhový pohyb, veľkosť lineárnej rýchlosti vložka bodu súvisí s uhlovou rýchlosťou W cez:

vložka = ΩR = 0.000023148 ​​s^-1'6300 km = 0.1458 km/s = 145.8 m/s

Dokonca aj neustály pohyb 145.8 m/s, Existuje zrýchlenie, ktoré poukazuje na stred kruhovej obežnej dráhy, zodpovedné za udržanie bodu v rotácii. Je to centripetálne zrýchlenie do_c, daná:

do_c = v² / R = (145.8 m/s)² / 6300 × 10³ m = 0.00337 m/s².

Odkazy

1. Giancoli, D. Fyzika. (2006). Zásady s aplikáciami. 6^th Sála. 22-25.
2. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa. 23 - 27.
3. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 21-22.
4. Rex, a. (2011). Základy fyziky. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Fyzika univerzity s modernou fyzikou. 14^th. Edimatizovať. Objem1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Vydanie. Mexiko. Redaktori učenia sa Cengage. 23-25.
7. Serway, r., Vulle, C. (2011). Základy fyziky. 9^nat Edimatizovať. Učenie sa. 43 - 55.
8. Wilson, J. (2011). Fyzika 10. Pearson Vzdelanie. 133 - 149.