Laplace transformovať

Aká je Laplaceova transformácia?

Ten Laplace transformovať Bolo to v posledných rokoch veľkého významu v inžinierstve, matematike, fyzike, okrem iných vedeckých oblastí, pretože okrem toho, že je veľmi zaujímavý o teoretický, poskytuje jednoduchý spôsob riešenia diferenciálnych rovníc a transformuje ich na algebraické rovnice.

Pôvodne Laplace Transformy predstavil Pierre-Simon Laplace (1745-1827) vo svojej štúdii o teórii pravdepodobnosti a v zásade sa považoval za matematický predmet iba teoretického záujmu.

Súčasné aplikácie vznikajú, keď sa rôzni matematici pokúsili dať formálne odôvodnenie „prevádzkových pravidiel“, ktoré používa Oliver Heaviside (1850-1925) pri štúdiu rovníc elektromagnetickej teórie.

Definícia transformácie Laplace

Nech f je definovaná funkcia pre t ≥ 0. Laplace transformácia je definovaná takto:

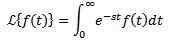
Hovorí sa, že Laplace transformácia existuje, ak sa predchádzajúci integrálny konvertuje, inak sa hovorí, že Laplace transformácia neexistuje.

Všeobecne platí, že označenie funkcie, ktorá je žiadaná na transformáciu malých písmen, a kapitálové písmeno zodpovedá jej transformácii. Týmto spôsobom budeme mať:

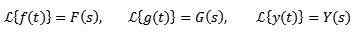
Príklady

Zvážte konštantnú funkciu f (t) = 1. Musíme sa transformovať:

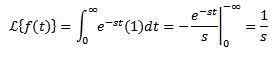
Za predpokladu, že integrál konvertuje, to znamená, že s> 0. Inak s < 0, la integral diverge.

Nech g (t) = t. Jeho Laplace transformácia je daná:

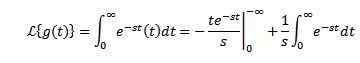
Pri integrácii podľa častí a poznať to^-Sv Má tendenciu 0, keď T má tendenciu nekonečno a s> 0, spolu s predchádzajúcim príkladom, ktorý musíme:

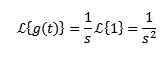
Transformácia môže alebo nemusí existovať, napríklad pre funkciu f (t) = 1/t, integrál, ktorý definuje jeho laplace transformáciu, sa konverguje, a preto jej transformované neexistuje.

Dostatočné podmienky na zabezpečenie toho, aby Laplace transformácia funkcie F existovala, je to, že F je v častiach nepretržitý pre t ≥ 0 a je exponenciálneho poriadku.

Hovorí sa, že funkcia je v častiach nepretržitá pre t ≥ 0, keď v akomkoľvek intervale [a, b] s a> 0, existuje konečný počet bodov t_{klimatizovať,} Kde f má diskontinuity a je nepretržitý v každom podinterve [t_K-1,tón_{klimatizovať}].

Na druhej strane sa hovorí, že exponenciálna funkcia C, ak existujú skutočné konštanty m> 0, c a t> 0, že:

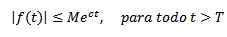
Ako príklady musíme f (t) = t² Je to exponenciálne, pretože | t²| < e^3T Pre všetky t> 0.

Formálne máme nasledujúcu vetu:

Veta (dostatočné podmienky na existenciu)

Ak F je kontinuálna funkcia pre t> 0 a exponenciálny C, potom je tu Laplace transformácia pre s> c.

Je dôležité zdôrazniť, že ide o stav dostatočnosti, to znamená, že by mohol existovať prípad, že existuje funkcia, ktorá tieto podmienky nespĺňa a napriek.

Príkladom je funkcia f (t) = t^-1/2 ktorý nie je v častiach nepretržitý pre t ≥ 0, ale jeho laplánová transformácia existuje.

Laplace transformácia niektorých základných funkcií

Nasledujúca tabuľka ukazuje Laplace transformácie najbežnejších funkcií.

Môže vám slúžiť: celé čísla

História Laplace Transform

Laplace transformácia dlhuje svoje meno Pierre-Simon Laplace, matematikovi a francúzskemu astronómovi a teoretikovi, ktorý sa narodil v roku 1749 a zomrel v roku 1827. Jeho sláva bola taká, že bol známy ako Newton vo Francúzsku.

V roku 1744 Leonard Euler (1707-1783) venoval svoje štúdie integrálom s formulárom

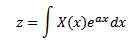
Ako riešenia bežných diferenciálnych rovníc, ale tento výskum rýchlo opustil. Neskôr Joseph Louis Lagrange (1736-1813), ktorý Eulera veľa obdivoval, tiež skúmal tento typ integrálu a súvisel s teóriou pravdepodobnosti.

1782, Laplace

V roku 1782 Laplace začal študovať tieto integrály ako riešenia diferenciálnych rovníc a podľa historikov sa v roku 1785 rozhodol preformulovať problém, ktorý neskôr porodil Laplaceove transformácie, ako sa dnes chápu.

Po zavedení v oblasti teórie pravdepodobnosti to bolo pre vedcov v okamihu malým záujmom a bolo považované iba za matematický objekt iba teoretického záujmu.

Oliver

Bolo to v polovici v polovici storočia, keď anglický inžinier Oliver Heaviside zistil, že diferenciálnymi operátormi sa dá považovať za algebraické premenné, čím sa ich moderné uplatňuje na Laplace Transformácie.

Oliver Heaviside bol fyzik, anglický elektrický a matematický inžinier, ktorý sa narodil v roku 1850 v Londýne a zomrel v roku 1925. Pri pokuse o riešenie problémov diferenciálnych rovníc aplikovaných na teóriu vibrácií a pomocou Laplaceho štúdie začalo formovať moderné aplikácie Laplay transformácie.

Výsledky vystavené Heavisidovi sa rozšírili rýchlo.

Užitočnosť práce Heaviside však pri riešení fyzikálnych rovníc spôsobila, že ich metódy boli populárne medzi fyzikmi a inžiniermi.

Napriek týmto neúspechom a po niekoľkých desaťročiach neúspešných pokusov by na začiatku 20. storočia mohlo byť poskytnuté prísne odôvodnenie prevádzkových pravidiel stanovených Heaviside.

Tieto pokusy sa vyplatili vďaka úsiliu rôznych matematikov, ako napríklad Bromwich, Carson, van der Pol,.

Laplace transformujú vlastnosti

Medzi vlastnosťami transformácie Laplace sa vyniká toto:

Linearita

Nech konštanta C1 a C2 a F (t) a g (t) funkcie, ktorých transformácie Laplace sú f (s) a g (s), potom musí:

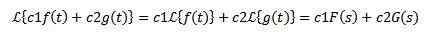
Z dôvodu tejto vlastnosti sa hovorí, že Laplace transformácia je lineárny operátor.

Príklad:

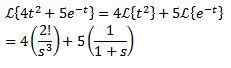
Prvá prekladová veta

Ak sa to stane, to:

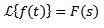
A 'a' je akékoľvek skutočné číslo, potom:

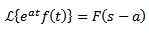
Príklad:

Ako Laplace de cos transformácia (2t) = s/(s^2 + 4) potom:

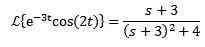
Veta druhej prekladu

Jo

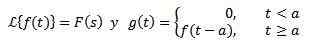
Tak

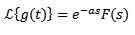
Príklad:

Ak f (t) = t^3, potom f (s) = 6/s^4. A preto transformácia 

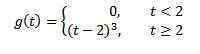
je g (s) = 6e^-2s/s^4

Zmena rozsahu

Jo

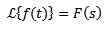
A „a“ je skutočne odlišný od nuly, musíme

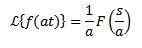
Príklad:

Pretože transformácia f (t) = sen (t) je f (s) = 1/(s^2 + 1)

Môže vám slúžiť: Vyvinutý zápis: Čo je, príklady a cvičenia

Laplace transformovaný z derivátov

Ak f, f ', f ", ..., f^(N) Sú nepretržité pre t ≥ 0 a sú exponenciálne a f^(N)(t) je v častiach nepretržitý pre t ≥ 0, potom

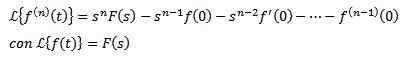
Integrálna Laplace transformuje

Jo

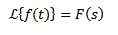
Tak

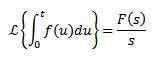
Násobenie tⁿ

Ak musíme

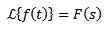
Tak

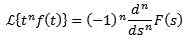
Rozdelenie t t

Ak musíme

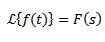
Tak

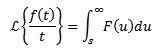
Periodické funkcie

Nech f je periodická funkcia s periódou t> 0, tj, f (t +t) = f (t), potom

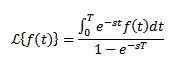
Správanie f (s), keď S má tendenciu nekonečno

Ak je f nepretržitý v častiach a exponenciálnom poradí a

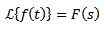
Tak

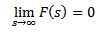
Inverzný transformovaný

Keď aplikujeme Laplace transformáciu na funkciu f (t), získame f (s), čo predstavuje uvedenú transformáciu. Rovnakým spôsobom môžeme povedať, že f (t) je transformácia inverzného laplace f (s) a je napísaná ako

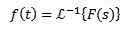
Vieme, že Laplace transformácie f (t) = 1 a g (t) = t sú f (s) = 1/s a g (s) = 1/s² preto musíme

Niektoré bežné Laplace transformované sú nasledujúce

Okrem toho je reverzná Laplace transformácia lineárna, to znamená, že je splnená

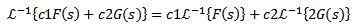
Cvičenie

Nájsť

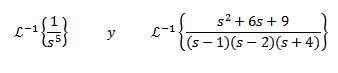
Aby sme vyriešili toto cvičenie, musíme sa zhodovať s funkciou F (S) s niektorými z predchádzajúcej tabuľky. V tomto prípade, ak vezmeme n + 1 = 5 a pomocou vlastnosti linearity reverznej transformácie vynásobíme a rozdelíme 4! Príchod

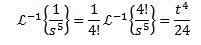
Pre druhú inverznú transformáciu aplikujeme čiastočné frakcie na prepísanie funkcie f (f) a potom vlastnosti linearity, získanie

Ako vidíme z týchto príkladov, je bežné, že hodnotené funkcie F (F) sa nezhodujú presne k žiadnej z funkcií uvedených v tabuľke. V týchto prípadoch, ako bolo pozorované, stačí prepísať funkciu, až kým nedosiahne správnu formu.

Laplace transformujú aplikácie

Diferenciálne rovnice

Hlavnou aplikáciou, ktorú Laplace transformuje, je riešenie diferenciálnych rovníc.

Pomocou vlastnosti transformácie derivátu je zrejmé, že

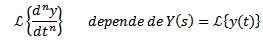
A z n-1 odvodeného vyhodnoteného pri t = 0.

Táto vlastnosť robí transformovanú.

Nasledujúce príklady ukazujú, ako použiť Laplace Transformáciu na riešenie diferenciálnych rovníc.

Príklad 1

Vzhľadom na nasledujúci problém s počiatočnou hodnotou

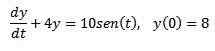
Na nájdenie riešenia použite Laplaceovu transformáciu.

Aplikujeme Laplaceovu transformáciu na každého člena diferenciálnej rovnice

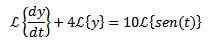
Pre majetok transformácie derivátu, ktorý máme

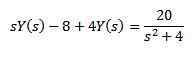
Pri vývoji všetkého výrazu a zúčtovania a (S) máme

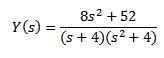
Použitie čiastočných frakcií na prepísanie pravej strany rovnice, ktorú získame

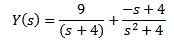
Naším cieľom je nájsť funkciu a (t), ktorá spĺňa diferenciálnu rovnicu. Pomocou inverznej laplace transformácie vedie k tomu

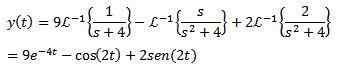
Príklad 2

Vyriešiť

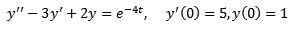
Rovnako ako v predchádzajúcom prípade uplatňujeme transformované na oboch stranách rovnice a samostatného termínu.

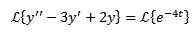
Týmto spôsobom máme v dôsledku toho

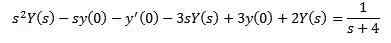
Výmena za počiatočné hodnoty a zúčtovanie a (s)

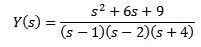
Použitím jednoduchých frakcií môžeme prepísať, ako nasleduje rovnica

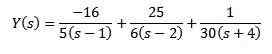
A použitie spätnej transformácie Laplace nám v dôsledku toho dáva

V týchto príkladoch bolo možné dosiahnuť nesprávny záver, že táto metóda nie je oveľa lepšia ako tradičné metódy na riešenie diferenciálnych rovníc.

Môže vám slúžiť: Pomer

Výhody, ktoré ponúka Laplace transformácia, je to, že to nie je potrebné.

Okrem toho pri riešení problémov s počiatočnou hodnotou touto metódou od začiatku používame počiatočné podmienky, takže na nájdenie konkrétneho riešenia nie je potrebné vykonať ďalšie výpočty.

Diferenciálne rovnice systémy

Laplace transformácia sa dá použiť aj na nájdenie riešení súčasných bežných diferenciálnych rovníc, ako je uvedené v nasledujúcom príklade.

Príklad

Vyriešiť

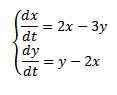
Pri počiatočných podmienkach x (0) = 8 e y (0) = 3.

Ak musíme

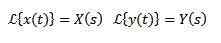
Tak

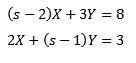
Riešenie nám dáva v dôsledku toho

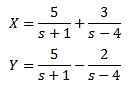
A pri aplikácii spätnej transformácie Laplace, ktorú máme

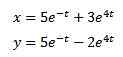
Mechanika a elektrické obvody

Laplace transformácia má vo fyzike veľký význam, má hlavne aplikácie pre mechaniku a elektrické obvody.

Jednoduchý elektrický obvod sa skladá z nasledujúcich prvkov:

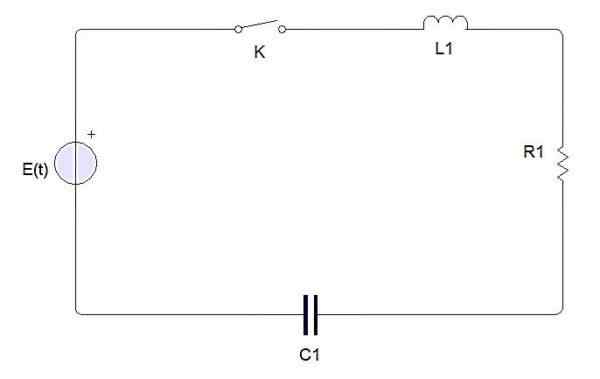Prvky elektrického obvodu

Spínač, batéria alebo zdroj, induktor, odpor a kondenzátor. Keď je spínač zatvorený elektrický prúd, ktorý označuje i (t). Zaťaženie kondenzátora je označené Q (T).

Podľa Kirchhoffovho druhého zákona musí napätie produkované Fuente e do uzavretého obvodu rovnať súčtu každého z vodopádov napätia.

Elektrický prúd i (t) súvisí s zaťažením q (t) v kondenzátore cez i = dq/dt. Na druhej strane pokles napätia v každom z prvkov je definovaný takto:

Pokles napätia v odporu je IR = R (DQ/DT)

Pokles napätia v induktore je L (di/dt) = l (d²Q/dt²)

Pokles napätia v kondenzátore je q/c

S týmito údajmi a uplatňovaním Kirchhoffovho druhého zákona na jednoduchý jednoduchý obvod sa získa diferenciálna rovnica druhého okruhu, ktorá opisuje systém a umožňuje nám určiť hodnotu q (t).

Príklad

Induktor, kondenzátor a odpor sú pripojené k batérii E, ako je to znázornené na obrázku. Induktor je 2 Henries, 0,02 Farads kondenzátor a 16 Onhmios rezistencie. Momentálne t = 0 uzatvára obvod. Nájdite zaťaženie a prúd kedykoľvek t> 0, ak e = 300 voltov.

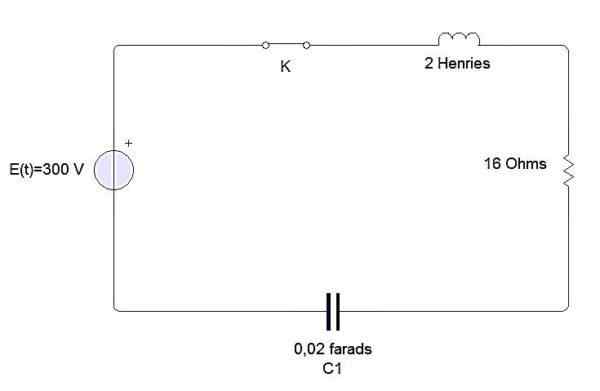
Máme, že diferenciálna rovnica opisujúca tento obvod je nasledovná:

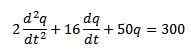
Kde počiatočné podmienky sú q (0) = 0, i (0) = 0 = q '(0).

Pri použití Laplaceovej transformácie to dostaneme

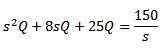
A zúčtovanie q (t)

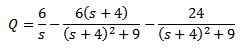
Potom, keď použijete inverznú laplace transformáciu, ktorú máme

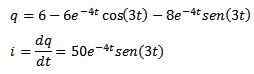
Odkazy

1. G.Holbrook, J. (1987). Laplace transformácia pre elektronických inžinierov. Limusa.
2. Ruiz, L. M., & Hernandez, m. P. (2006). Diferenciálne a transformované rovnice Laplace s aplikáciami. Redakcia.
3. Simmons, G. F. (1993). Diferenciálne rovnice s historickými aplikáciami a poznámkami. McGraw-Hill.
4. Spiegel, m. R. (1991). Laplace sa zmenil. McGraw-Hill.
5. Zill, D. G., & Cullen, m. R. (2008). Diferenciálne rovnice s hodnotami cenných papierov na hranici. Cengage Learning Editor, s.Do.