Vlastnosti Fourierovej transformácie, aplikácie, príklady

Ten Fourierovu transformáciu Je to metóda analytickej primeranosti zameranej na integrovateľné funkcie, ktoré patrí do rodiny Tkomplexný výkupný. Pozostáva z redefinície funkcií F t) Pokiaľ ide o cos (t) a sen (t).

Trigonometrické identity týchto funkcií spolu s ich charakteristikami derivácie a antidevácie slúžia na definovanie Fourierovej transformácie prostredníctvom nasledujúcej komplexnej funkcie:

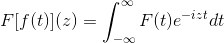
Ktorý je splnený, zatiaľ čo výraz má zmysel, to znamená, keď je nesprávny integrál konvergentný. Algebraicky sa hovorí, že Fourierovu transformáciu je lineárny homeomorfizmus.

Akákoľvek funkcia, ktorú je možné prepracovať s Fourierovou transformáciou, musí predstavovať neplatnosť mimo definovaného parametra.

[TOC]

Vlastnosti

Zdroj: pexels

Fourierova transformácia spĺňa tieto vlastnosti:

Existencia

Na overenie existencie Fourierovej transformácie na funkciu F (T) definovanú v kráľovských kráľovoch R, Musia byť splnené nasledujúce 2 axiómy:

1. f (t) je nepretržitý na kúsky pre všetko R
2. f (t) je integrovateľné do R

Linearita Fourierovej transformácie

Nech m (t) a n (t) dve dve funkcie s definovanými Fourierovou transformovanou, s konštantami A a b.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Čo sa tiež spolieha na linearita integrálu rovnakého mena.

Fourier transformovaný z derivátu

Máte funkciu F  čo je nepretržité a integrovateľné vo všetkých reais, kde:

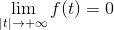
A derivát F (f ') Je nepretržitý a definovaný na kúsky vo všetkom R

Fourierova transformácia derivátu je definovaná integráciou časťami, nasledujúcim výrazom:

F [f '(t)] (z) = IzF [f (t)] (z)

Pri deriváciách vyššieho poriadku sa bude uplatňovať homológne, kde pre všetky n 1 musíte:

F [f ⁿ'(t)] (z) = (iz)ⁿF [f (t)] (z)

Diferenciácia Fourierovej transformácie

Máte funkciu F  čo je nepretržité a integrovateľné vo všetkých reais, kde:

I (d/dz)F [f (t)] (z) = F  [t .  f (t)] (z)

Fourier transformovaný z prekladu

Pre všetkých θ ktorý patrí do súboru a Tón To patrí do súboru S ', musíte:

F [ τ_do 9] =  a^-Iay F [ θ]                                 F [ τ_doTón ] =  a^-Iax  F [ T]   

S  τ_do  pracuje ako prevádzkovateľ prekladu na vekto.

Preklad Fourierovej transformácie

Pre všetkých θ ktorý patrí do súboru a Tón To patrí do súboru S ', musíte:

τ_do F [9] =  F [a^-Iax.θ]                                τ_do F [t ] =  F [a^-Iay . T]

Môže vám slúžiť: Hypercubo: Definícia, rozmery, súradnice, rozvinuté

Pre všetkých do čo patrí R

Fourierova transformácia skupiny mierky

Pre všetkých θ ktorý patrí do súboru S. Tón to patrí do set s '

λ patriaci R - 0  Musíš:

F [θ (λx)] = (1 / | λ |) F [9] (a/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (a/λ)

Jo F Je to nepretržitá a čisto integrovateľná funkcia, kde a> 0. Tak:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Aby sme preukázali tento výsledok, môžeme pokračovať v zmene premennej.

Keď t → + potom s = pri → + ∞

Keď t → - potom s = at → - ∞

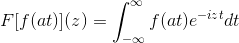
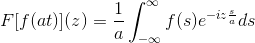
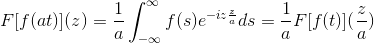
Symetria

Študovať symetriu Fourierovej transformácie.

Máte 9 a δ, ktoré patria Siež. Odtiaľ sa dá odvodiť, že:

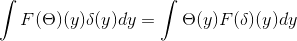
Získanie

1 / (2π)^d  F [9 ], F [δ] Parseval Identita

1 / (2π)^D/2  || F [9 ] ||_L²_R^d     Plancherel

Fourier sa transformoval z produktu na konvolúciu

Prenasledovanie podobných cieľov, ktoré sa v Laplace transformujú, konvolúcia funkcií sa vzťahuje na produkt medzi jeho Fourier Transforps.

Má F a G ako 2 funkcie obmedzené, definované a úplne integrovateľné:

F (f *g) = f (f) . F (g)

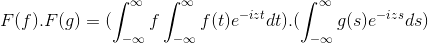
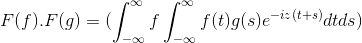
Potom pri zmene premennej

t + s = x; Dvojitý integrálny dvojitý integrál pokračuje

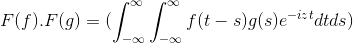
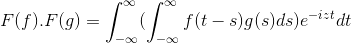
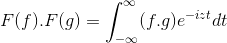
F (f) . F (g) = f (f . g)

Kontinuita a spadnutie do nekonečna

Pre všetkých 9, ktoré patrí R, f [ 9] dodržiava kritériá kontinuálnej funkcie obmedzené v r^d.

Tiež F [ θ] (y) → 0 v C SI | y | → ∞

História

Tento matematický koncept predstavil Joseph B. Fourier v roku 1811 pri vývoji zmluvy týkajúcej sa Roztiahnutie tepla. Rýchlo ho prijali rôzne odvetvia vedy a inžinierstva.

Bol založený ako hlavný pracovný nástroj v štúdiu rovníc s čiastočnými derivátmi, v porovnaní s pracovným vzťahom medzi Laplace transformované a bežné diferenciálne rovnice.

Čo je Fourierov transformácia pre?

Slúži hlavne pre významné rovnice, pri.

Pri optimalizácii, modulácii a modelovaní výsledkov pôsobí ako štandardizovaný výraz, ktorý je častým zdrojom pre inžinierstvo po niekoľkých generáciách.

Fourierova séria

Sú definované série z hľadiska Cosen a prsníkov; Slúžia na uľahčenie práce so všeobecnými periodickými funkciami. Pri použití sú súčasťou techník rozlíšenia čiastočných a bežných diferenciálnych rovníc.

Môže vám slúžiť: skutočná skutočná premenná funkcia a jej grafická reprezentácia

Fourier Series je ešte všeobecnejší ako séria Taylor, pretože vyvíjajú periodické funkcie diskontinua, ktoré nemajú žiadne zastúpenie v sérii Taylor.

Ostatné formy série Fourier

Analyticky porozumieť Fourierovej transformácii je dôležité.

-Fourier Series na funkcii 2L obdobia

Mnohokrát je potrebné prispôsobiť štruktúru Fourierovej série na periodické funkcie, ktorých obdobie je p = 2l> 0 v intervale [-l, l].

-Fourier Series v párnych a nepárnych funkciách

Zvažuje sa interval [-π, π], ktorý ponúka výhody pri využívaní symetrických charakteristík funkcií.

Ak F je krútiaci moment, séria Fourier je zriadená ako séria Cosenosu.

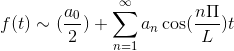
Ak je F nepárne, séria Fourier je zriadená ako séria prsníkov.

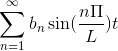
-Komplexná notácia série Fourier

Ak máte funkciu F (T), ktorá spĺňa všetky vyvinuté požiadavky série Fourier, je možné ju označiť v intervale [-T, t] pomocou svojej komplexnej zápisu:

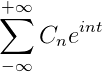
Žiadosti

Zdroj: pexels

Výpočet základného riešenia

Fourierova transformácia je silný nástroj v štúdiu čiastočných diferenciálnych rovníc lineárneho typu s konštantnými koeficientmi. Žiadajte o funkcie s doménami, ktoré nie sú obmedzené rovnako.

Rovnako ako Laplace transformácia, Fourier Transformácia transformuje funkciu čiastočných derivátov, na bežnú diferenciálnu rovnicu, ktorá je oveľa ľahšie fungovať.

Problém Cauchy pre tepelnú rovnicu predstavuje časté pole aplikácie Fourierovej transformácie, kde sa generuje funkcia Dirichlet Heat alebo jadro jadra.

Pokiaľ ide o výpočet základného riešenia, sú uvedené nasledujúce prípady, ak je bežné nájsť Fourierovu transformáciu:

-Laplaceová rovnica

-Tepelná rovnica

-Schrödingerova rovnica

-Vlnová rovnica

Teória signálu

Všeobecný dôvod uplatňovania Fourierovej transformácie v tejto vetve je väčšinou spôsobený charakteristickým rozkladom signálu ako nekonečného prekrývania ľahšie liečiteľných signálov.

Môže to byť zvuková vlna alebo elektromagnetická vlna, Fourierova transformácia ju vyjadruje v jednoduchých prekrývaní vlny. Táto reprezentácia je v elektrotechnike pomerne častá.

Môže vám slúžiť: vertikálna čiara

Na druhej strane sú príkladmi aplikácie Fourierovej transformácie v oblasti teórie signálu:

-Problémy s identifikáciou systému. Zavedené f a g

-Problém s konzistentnosťou výstupného signálu

-Problémy s filtrovaním signálu

Príklady

Príklad 1

Definujte Fourierovu transformáciu pre nasledujúci výraz:

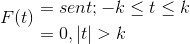
Môžeme to tiež reprezentovať takto:

F (t) = Hriech (t) [h_{(T + k)} - H_{(T - k)} ]

Je definovaný obdĺžnikový impulz:

p (t) = h_{(T + k)} - H_{(T - k)}

Fourierova transformácia sa aplikuje na ďalší výraz, ktorý sa podobá vete modulácie.

f (t) = p (t) sin (t)

Kde: F [w] = (1/2) I [p (w + 1) - p (w - 1)]

A Fourierovská transformácia je definovaná:

F [w] =  (1/2) I [(2/2W+1) Sen (k (w+1)) - (2/2W+1) Sen (K (W-1))]

Príklad 2

Definujte Fourierovu transformáciu pre expresiu:

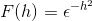Podľa definície vyjadrujeme transformáciu nasledovne

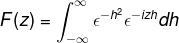
Pretože f (h) je rovnomerná funkcia, možno to potvrdiť

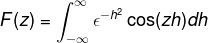Odvodenie v rámci integrálu vzhľadom na z sa dá výraz prepísať. Tento krok je významný pri práci s diferenciálnymi rovnicami.

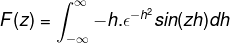
Integrácia podľa častí sa používa výberom premenných a ich diferenciálov nasledovne

u = sin (zh) du = z cos (zh) dh

dv = h (e^-h)²                       V = (e^-h)² / 2

Nahradenie

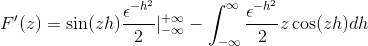
Po vyhodnotení podľa základnej vety výpočtu

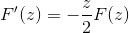
Pri použití predchádzajúcich znalostí týkajúcich sa diferenciálnych rovníc prvého poriadku je výraz označený ako

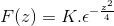
Aby sme dostali k hodnoteniu 

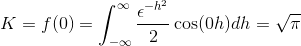
Nakoniec je Fourierove transformácia definované ako

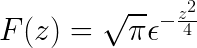
Navrhované cvičenia

• Stanovte expresiu Fourierovej transformácie
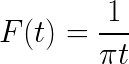
• Vyriešte nasledujúci nesprávny integrál pomocou Paresevalovej rovnosti
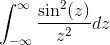
• Získajte transformáciu výrazu s (1+w²)

Odkazy

1. Duoandikoetxea Zuazo, J., Fourierová analýza. Addison-Wesley Iberoamericana, Autonómna univerzita v Madride, 1995.
2. Levy, j. L., Matematická analýza a numerické metódy pre vedu a techniku. Springer-Verlag, 1990.
3. Lieb, e. H., Gaussovské jadrá majú iba gaussovské maximalizátory. Vynájdenie. Matematika. 102, 179-208, 1990.
4. Dym, h., McKean, h. P., Fourierové série a integrály. Academic Press, New York, 1972.
5. Schwartz, L., Distribúcie Théorie des. Edimatizovať. Hermann, Paríž, 1966.