Izometrické transformácie

Ten izometrické transformácie Sú to zmeny polohy alebo orientácie určitého čísla, ktoré nemenia tvar alebo veľkosť tohto. Tieto transformácie sú klasifikované na tri typy: preklad, rotácia a odraz (izometria). Geometrické transformácie vo všeobecnosti umožňujú vytvoriť novú postavu z iného daného.

Transformácia na geometrickú postavu znamená, že nejakým spôsobom bola podrobená určitej zmene; to znamená, že sa zmenilo. Podľa pocitu originálu a podobných v rovine je možné geometrické transformácie rozdeliť na tri typy: izometrické, izomorfné a anamorfické.

Charakteristiky izometrických transformácií

- Izometrické transformácie sa vyskytujú, keď sú zachované veľkosti segmentov a uhlov medzi pôvodným obrázkom a transformovaným obrázkom.

- Pri tomto type transformácie sa forma alebo veľkosť čísla nezmenia (sú zhodné), ide iba o zmenu polohy, či už v orientácii alebo v zmysle. Týmto spôsobom budú počiatočné číslo a finále podobné a geometricky zhodné.

- Izometria sa vzťahuje na rovnosť; To znamená, že geometrické čísla budú izometrické, ak budú mať rovnaký tvar a veľkosť.

- Pri izometrických transformáciách je jediné, čo sa dá pozorovať. Toto číslo sa nazýva homológny (podobný) originálu.

- Existujú tri typy pohybov, ktoré klasifikujú izometrickú transformáciu: preklad, rotáciu a odraz alebo symetria.

Typy izometrických transformácií

Prekladom

Sú tie izometrie, ktoré umožňujú premiestniť v priamke všetky body roviny v konkrétnom smere a vzdialenosti.

Ak sa číslo translatuje transláciou, nemení svoju orientáciu vo vzťahu k počiatočnej polohe, ani nestráca svoje vnútorné opatrenia, opatrenia jeho uhlov a bočných strán. Tento typ posunu je definovaný tromi parametrami:

• Adresa, ktorá môže byť vodorovná, vertikálna alebo šikmá.
• Smer, ktorý môže byť vľavo, vpravo, hore alebo dole.
• Vzdialenosť alebo veľkosť, čo je dĺžka, ktorá je od počiatočnej polohy do finále ktoréhokoľvek bodu, ktorý sa pohybuje.

Môže vám slúžiť: Curtóza: Definícia, typy, vzorce, na čo je napríklad

Aby sa izometrická transformácia v dôsledku prekladu, musí spĺňať nasledujúce podmienky:

• Obrázok musí vždy udržiavať všetky svoje rozmery, lineárne aj uhlové.
• Obrázok nemení svoju polohu vzhľadom na horizontálnu os; to znamená, že jeho uhol sa nikdy nelíši.
• Preklady budú vždy zhrnuté v jednom, bez ohľadu na počet vykonaných prekladov.

V rovine, kde je stred alebo, s súradnicami (0,0), je preklad definovaný vektorom t (a, b), čo naznačuje posunutie počiatočného bodu. To znamená:

P (x, y) + t (a, b) = p '(x + a, y + b)

Napríklad, ak sa použije v súradnicovom bode P (8, -2) Translation t (-4, 7), získa sa:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

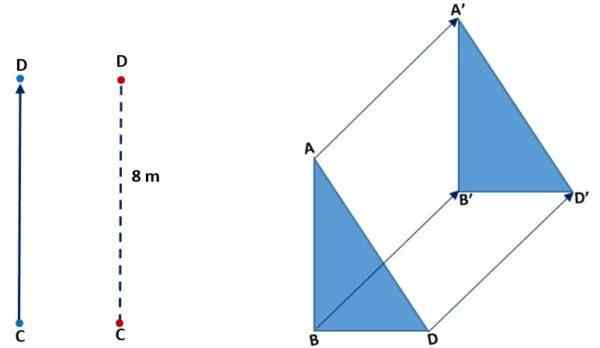
Na nasledujúcom obrázku (vľavo) môžete vidieť, ako sa bod C presunul a zhodoval sa s D. Urobil to vertikálne, význam stúpol a CD vzdialenosť alebo veľkosť bola 8 metrov 8 metrov. Na správnom obrázku sa pozoruje preklad trojuholníka:

Rotáciou

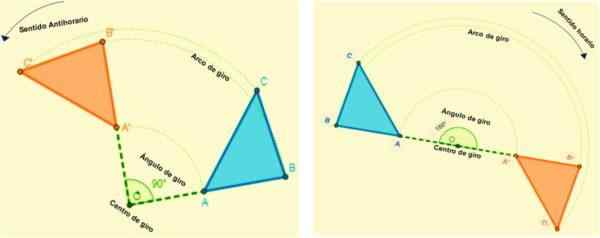
Sú tie izometrie, ktoré umožňujú postavu otočiť všetky body lietadla. Každý bod sa otočí po oblúku, ktorý má stanovený konštantný uhol a stanovený pevný bod (stredisko otáčania).

To znamená, že všetka rotácia bude definovaná jeho rotáciou a stredom otáčania uhla. Keď sa číslo transformuje rotáciou, udržuje mieru svojich uhlov a bočných strán.

Rotácia sa vyskytuje v určitom smere, je pozitívna, keď je otočenie anti -horč.

Ak sa bod (x, y) otáča vzhľadom na pôvod -to je, jeho rotačný stred je (0,0) -, v uhle 90^ani 360^ani Súradnice bodov budú:

Môže vám slúžiť: Štatistické vetvy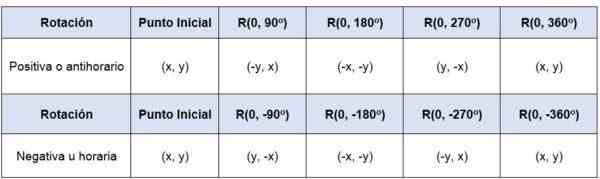

V prípade, že rotácia nemá na začiatku, musí sa preniesť pôvod súradníckeho systému k novému pôvodu.

Napríklad, ak sa použije bod P (-5,2), 90 rotácií^ani, Okolo pôvodu a v pozitívnom zmysle budú jeho nové súradnice (-2,5).

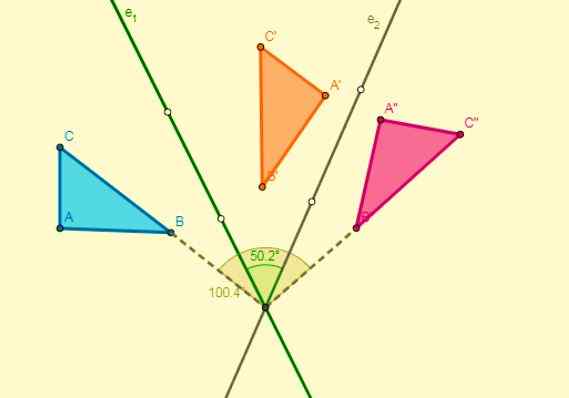
Odrazom alebo symetriou

Sú tie transformácie, ktoré investujú body a čísla roviny. Táto investícia môže byť z hľadiska bodu alebo môže byť tiež vzhľadom na čiaru.

Inými slovami, v tomto type transformácie je každý bod v pôvodnom obrázku spojený s iným bodom (obrázok) homológnej postavy, takže bod a jeho obraz sú v rovnakej vzdialenosti od čiary nazývanej osi symetrie.

Ľavá časť postavy bude teda odrazom pravej strany bez zmeny jej tvaru alebo rozmerov. Symetria transformuje rovnakú postavu, ale naopak, ako je vidieť na nasledujúcom obrázku:

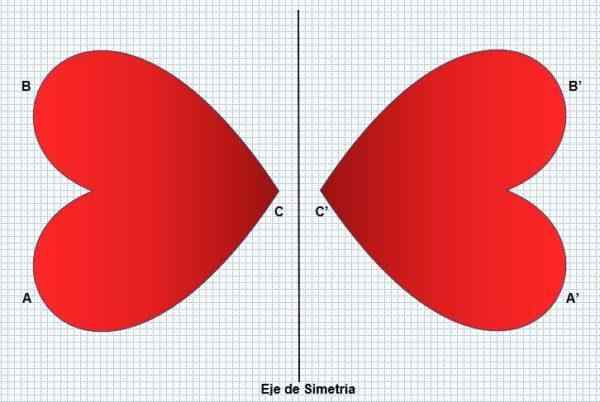
Symetria je prítomná v mnohých aspektoch, ako sú napríklad niektoré rastliny (slnečnice), zvieratá (páv) a prírodné javy (snehové vločky). Ľudská bytosť to odráža vo svojej tvári, ktorá sa považuje za faktor krásy. Odraz alebo symetria môže byť dvoch typov:

Centrálna symetria

Je to tá transformácia, ktorá sa vyskytuje s ohľadom na bod, v ktorom môže číslo zmeniť svoju orientáciu. Každý bod v pôvodnom obrázku a jeho obraz je v rovnakej vzdialenosti od bodu alebo, nazývaný Symetry Center. Symetria je ústredná, keď:

• Bod aj jeho obraz a stred patria do tej istej línie.
• S rotáciou 180^ani Zarobí sa zo stredu alebo postavy rovnajúcej sa originálu.
• Ťahy počiatočného obrázku sú rovnobežné s ťahmi vytvoreným obrázkom.
• Význam obrázku sa nemení, vždy bude v harmonograme.

Môže vám slúžiť: Koľko musíte pridať do 3/4, aby ste dostali 6/7?

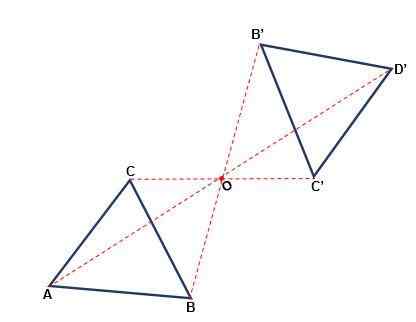Axiálna symetria

Táto transformácia sa vyskytuje vzhľadom na os symetrie, kde každý bod v počiatočnom obrázku je spojený s iným bodom v obraze a tieto sú v rovnakej vzdialenosti ako os symetrie. Symetria je axiálna, keď:

• Segment, ktorý spája bod s jeho obrazom.
• Čísla menia svoj význam týkajúci sa smeru alebo časového smeru.
• Rozdelením postavy centrálnou čiarou (os symetrie) sa jedna z výsledných polovíc zhoduje s inou polovicou.

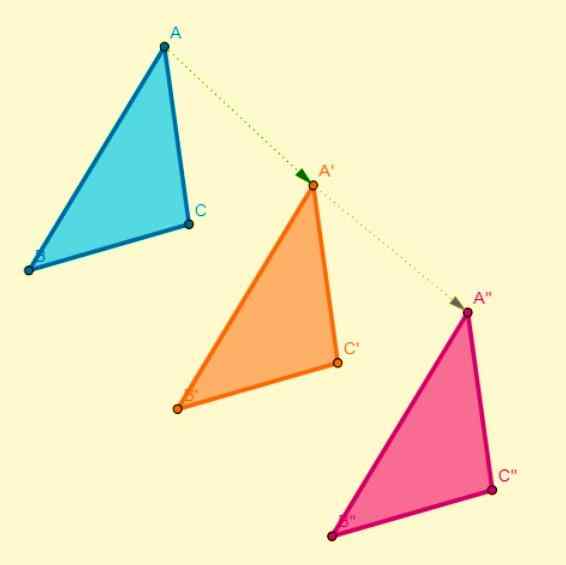
Kompozícia

Zloženie izometrických transformácií sa vzťahuje na postupné uplatňovanie izometrických transformácií na rovnakom obrázku.

Zloženie prekladu

Zloženie dvoch prekladov vedie k inému prekladu. Ak sa vykonáva v rovine, na vodorovnej osi (x) sa menia iba súradnice tejto osi, zatiaľ čo súradnice vertikálnej os (y) zostávajú rovnaké a naopak.

Zloženie rotácie

Zloženie dvoch zákrut s rovnakým centrom vedie k inému zákrut, ktoré má rovnaké centrum a ktorého amplitúda bude súčtom amplitúd týchto dvoch zákrut.

Ak má zákruty v strede iného stredu, rez z dvoch segmentov podobných bodov bude stredom rotácie.

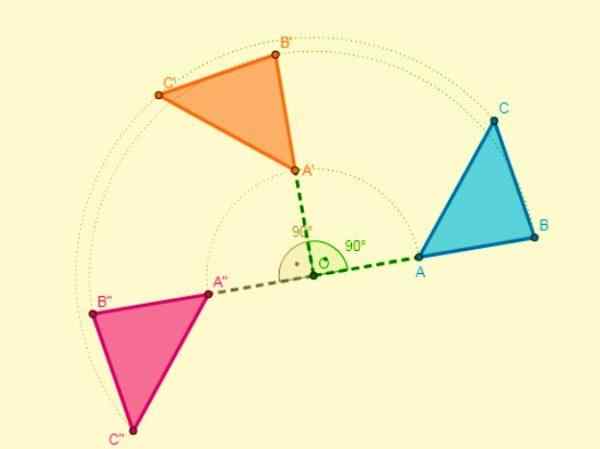
Zloženie symetrie

V tomto prípade bude zloženie závisieť od toho, ako sa uplatňuje:

• Ak sa rovnaká symetria aplikuje dvakrát, výsledkom bude identita.
• Ak sa použijú dve symetrie s ohľadom na dve paralelné osi, výsledkom bude preklad a ich posun je dvojnásobok vzdialenosti týchto osí:

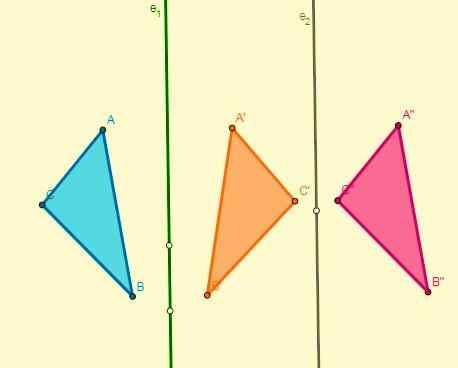
• Ak sa použijú dve symetrie vzhľadom na dve osi, ktoré sú rezané v bode O (stred), získa sa rotácia so stredom a jeho uhol bude dvojnásobkom uhla, ktorý sa tvoria osi: