Homoticia

Ten Homoticia Ide o geometrickú zmenu v rovine, kde sa z pevného bodu nazývaného stred (O) vynásobia násobenie spoločným faktorom. Týmto spôsobom každý bod P zodpovedá inému bodu transformácie a tieto sú zarovnané s bodom alebo.

Potom je homotecia korešpondencia medzi dvoma geometrickými číslami, kde sa transformované body nazývajú homotetické a tieto sú zarovnané s pevným bodom a navzájom paralelné segmenty.

Vysvetlenie a vzorec

Homotecia je transformácia, ktorá nemá zhodný obraz, pretože z obrázku získajú jednu alebo viac čísel väčšej alebo menšej veľkosti ako pôvodný obrázok; to znamená, homotecia transformuje mnohouholník na iný podobný.

Aby sa splnila homoticia, musí zodpovedať bodom až point a priamka, aby páry homológnych bodiek boli zarovnané s tretím pevným bodom, ktorý je stredobodom Homotecia.

Podobne by mali byť rovnobežné páry čiary, ktoré sa zjednocujú. Vzťah medzi takýmito segmentmi je konštanta nazývaná Homotecia (K) dôvod; takým spôsobom, že homotecia možno definovať ako:

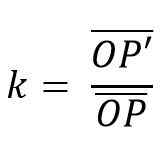
Aby sa tento typ transformácie uskutočnil, začína ľubovoľný bod, ktorý bude stredobodom Homotecia.

Z tohto bodu sú segmenty čiary nakreslené pre každý vrchol obrázku, ktorý sa má transformovať. Stupnica, na ktorej sa vytvára reprodukcia nového čísla, je uvedená z dôvodu homotecie (k).

Vlastnosti homotiecie

Jednou z hlavných vlastností homotecia je to, že z dôvodu homotécie (k) sú všetky homotické postavy podobné. Medzi ďalšie vynikajúce vlastnosti patria:

Môže vám slúžiť: Zložená proporcionalita: Vysvetlenie, tri zložené pravidlo, cvičenia

- Homotecia centrum (O) je jediný dvojitý bod a transformuje sa; to znamená, že sa nemení.

- Čiary, ktoré prechádzajú centrom, sa stávajú sami sebou (sú dvojnásobné), ale body, ktoré ho zostavujú, nie sú dvojnásobné.

- Čiary, ktoré neprechádzajú stredom, sa transformujú na rovnobežné čiary; Týmto spôsobom sú uhly homotiecie rovnaké.

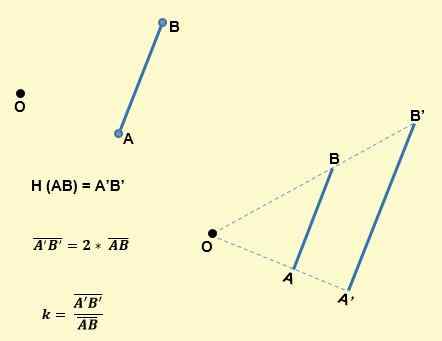
- Obrázok segmentu strednou homotecia alebo dôvod k, je segment rovnobežný s ním a má K násobok jeho dĺžky. Napríklad, ako je vidieť na nasledujúcom obrázku, segment AB pre homoteciu bude ďalším segmentom A'B ', takže AB bude rovnobežný s A'b' a K bude:

- Homotické uhly sú zhodné; to znamená, že majú rovnaké opatrenie. Preto obraz uhlu je uhol, ktorý má rovnakú amplitúdu.

Na druhej strane, homotecia sa musí meniť v závislosti od hodnoty svojho dôvodu (k) a môžu sa vyskytnúť nasledujúce prípady:

- Ak konštanta k = 1, všetky body sú stanovené, pretože sa transformujú. Homotetická postava sa teda zhoduje s originálom a transformácia sa bude nazývať funkcia identity.

- Ak k ≠ 1, jediným pevným bodom bude centrum Homotecia (o).

- Ak k = -1, homotecia sa stáva centrálnou symetriou (C); To znamená, že sa objaví rotácia okolo C, pod uhlom 180^ani.

- Ak k> 1, veľkosť transformovaného čísla bude väčšia pre veľkosť originálu.

Môže vám slúžiť: Iracionálne čísla: História, vlastnosti, klasifikácia, príklady

- Áno 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Áno -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Áno k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Typy homotecie

Homotecia by sa mohla tiež rozdeliť do dvoch typov v závislosti od hodnoty svojho dôvodu (k):

Priamy homoticia

Vyskytuje sa, ak konštanta k> 0; To znamená, že homotické body sú na rovnakej strane vzhľadom na centrum:

Faktor proporcionality alebo pomer podobnosti medzi priamymi homotickými hodnotami bude vždy pozitívny.

Inverzná homotecia

Sa vyskytuje, ak konštanta k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

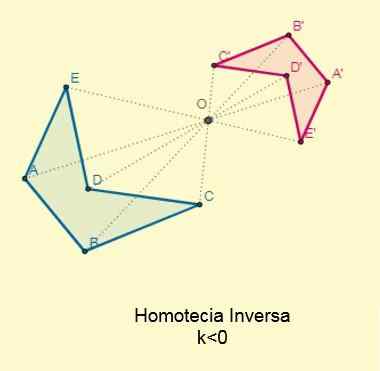
Faktor proporcionality alebo pomer podobnosti medzi inverznými homotickými hodnotami bude vždy negatívny.

Kompozícia

Keď sa postupne vykonáva niekoľko pohybov, až kým sa postava rovná originálu, dochádza k zloženiu pohybov. Zloženie niekoľkých pohybov je tiež pohyb.

Zloženie medzi dvoma homoteciami vedie k novej homotecia; To znamená, že existuje produkt homotecia, v ktorom bude centrum v súlade s centrom dvoch pôvodných transformácií a dôvod (k) je produktom týchto dvoch dôvodov.

Tak, v zložení dvoch homotíc h₁(Buď₁, klimatizovať₁) a h₂(Buď₂, klimatizovať₂), Násobenie vašich dôvodov: K₁ x k₂ = 1 bude mať za následok homoticiu rozumu K₃ = K₁ x k₂. Centrum tejto novej homotecie (alebo₃) sa nachádza na linke alebo₁ Ani₂.

Môže vám slúžiť: opačné uhly pri vrchole (s vyriešeným cvičením)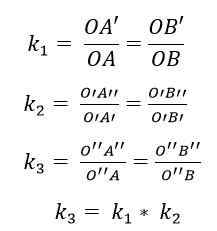

Homotecia zodpovedá byte a nezvratnej zmene; Ak sa uplatňujú dve homotécie, ktoré majú rovnaké centrum a dôvod, ale s iným znakom, pôvodný obrázok sa získa.

Príklady homotiecie

1. Prvý príklad

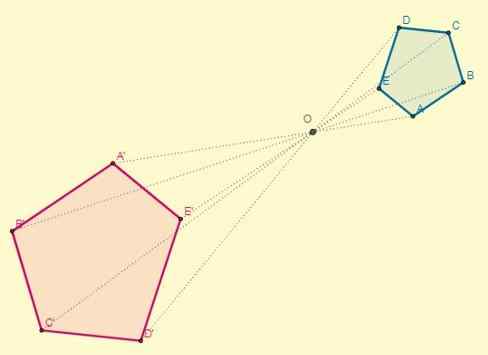
Aplikujte homoteciu na daný polygón v strede (O), ktorý sa nachádza 5 cm od bodu A a ktorého dôvodom je K = 0,7.

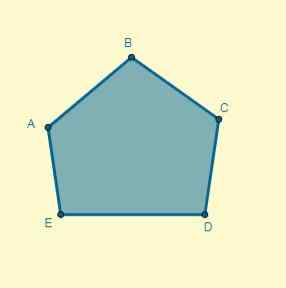
Riešenie

Akýkoľvek bod sa vyberie ako centrum homotecie, a z toho sa obchodujú s vrcholmi obrázku:

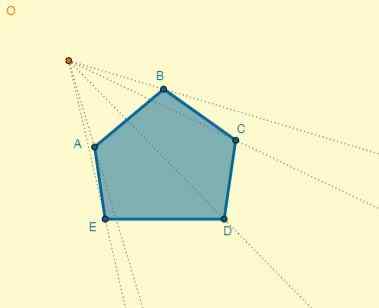
Vzdialenosť od stredu (O) do bodu A je OA = 5; Vďaka tomu môžete určiť vzdialenosť jedného z homotických bodov (OA ') a tiež s vedomím, že k = 0,7:

Oa '= k x oa.

OA '= 0,7 x 5 = 3,5.

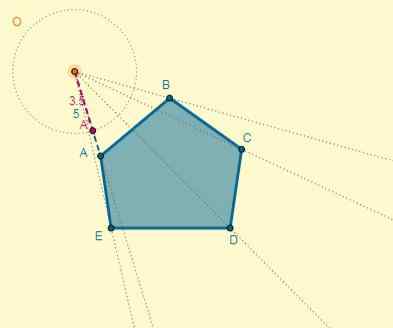
Proces je možné vykonať pre každý vrchol, alebo môžete tiež nakresliť homotický polygón, ktorý si pamätá, že dva polygóny majú paralelné strany:

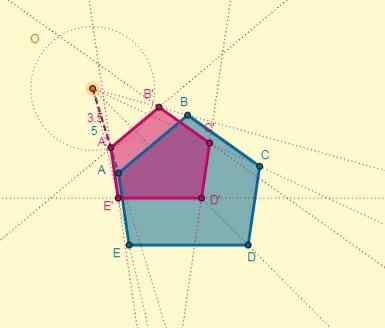
Nakoniec sa transformácia vidí takto:

2. Druhý príklad

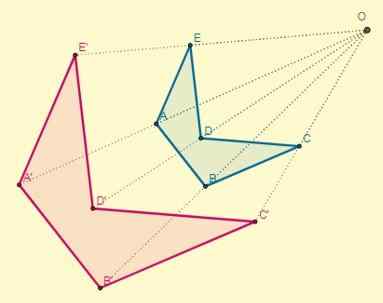
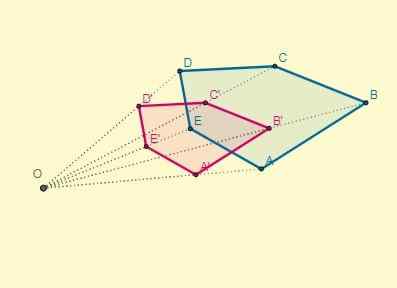
Aplikujte homoteciu na daný polygón v strede (O), ktorý sa nachádza 8,5 cm od bodu C a ktorého a dôvod K = -2.

Riešenie

Vzdialenosť od stredu (O) do bodu C je OC = 8,5; S týmito údajmi je možné určiť vzdialenosť jedného z homotických bodov (OC '), tiež s vedomím, že k = -2:

OC '= K X OC.

OC '= -2 x 8,5 = -17

Po nakreslení segmentov vrcholov transformovaného polygónu sú počiatočné body a ich homotetika umiestnené na opačných koncoch vzhľadom na stred: