Fyzický

Zákony o prenose tepla, formy prenosu, príklady

Zákony o prenose tepla, formy prenosu, príklady

Existuje prenos tepla Keď energia ide z jedného tela na druhé kvôli teplotnému rozdielu medzi nimi. Proces prenosu tepla prestane hneď po vyrovnávaní teploty tela v kontakte alebo keď je kontakt medzi nimi potlačený.

Množstvo energie prenesenej z jedného tela do druhého v určitom časovom období sa nazýva Prenájmy tepla. Jedno telo môže dať teplo inému, alebo ho môže absorbovať, ale teplo vždy prechádza z tela najvyššej teploty na najnižšiu teplotu.

postava 1. V ohňu sú uvedené tri mechanizmy prenosu tepla: jazda, konvekcia a žiarenie. Zdroj: Pixabay.

Tepelné jednotky sú rovnaké ako jednotky energie a v medzinárodnom systéme opatrení (SI) je Joule (J). Ostatné často používané tepelné jednotky sú kalórie a btu. 

Pokiaľ ide o matematické zákony, ktoré upravujú prenos tepla, závisia od mechanizmu, ktorý zasahuje do výmeny. 

Keď sa teplo vykonáva z jedného tela do druhého, rýchlosť, s akou sa vymieňa teplo, je úmerná teplotnému diferenciálu. Toto je známe ako Fourierov zákon tepelnej vodivosti, čo vedie k Zákon o chladení v Newtone.

[TOC]

Formy/mechanizmy prenosu tepla

Sú to spôsoby, ako sa dá teplo vymieňať medzi dvoma telami. Uznávajú sa tri mechanizmy:

-Jazdný

-Konvekcia

-Žiarenie

V hrnci, ako je ten, ktorý je uvedený na obrázku vyššie, sú tieto tri mechanizmy prenosu tepla:

-Kov hrnca sa zahrieva hlavne jazdou.

-Voda a vzduchové teplo a stúpanie konvekciou.

-Ľudia v blízkosti hrnca sú zahrievané emitovaným žiarením.

Jazdný

Vedenie tepla sa vyskytuje väčšinou v tuhých látkach a najmä v kovoch.

Napríklad kuchynský roh vysiela teplo do jedla vo vnútri hrnca cez kovový mechanizmus a kovové steny nádoby. V tepelnom vedení nedochádza k prenosu materiálu, iba energia.

Konvekcia

Mechanizmus konvekcie je typický pre kvapaliny a plyny. Takmer vždy sú to menej husté pri vyššej teplote, z tohto dôvodu dochádza k prenosu tepla v stúpajúcom zmysle najhorúcejšej tekutiny do vysokých oblastí s najchladnejšou tekutinou. V mechanizme konvekcie je prenos materiálu. 

Môže vám slúžiť: Nestabilná rovnováha: Koncept a príklady

Žiarenie

Pokiaľ ide o svoju časť, mechanizmus žiarenia umožňuje výmenu tepla medzi dvoma telami, aj keď nie sú v kontakte. Okamžitým príkladom je slnko, ktoré zahrieva zem cez prázdny priestor medzi nimi. 

Všetky telá emitujú a absorbujú elektromagnetické žiarenie. Ak máte dve telá pri rôznych teplotách, dokonca aj vo vákuu, po chvíli dosiahnu rovnakú teplotu v dôsledku kalorickej výmeny elektromagnetického žiarenia.

Rýchlosť prenosu

V termodynamických systémoch v rovnováhe dovážuje množstvo celkového tepla vymeneného s prostredím, takže systém prechádza z jednej rovnováhy na druhú.

Na druhej strane, prenos tepla, záujem sa zameriava na prechodný jav, keď systémy ešte nedosiahli tepelnú rovnováhu. Je dôležité poznamenať, že množstvo tepla sa vymení v určitom časovom období, to znamená, že existuje rýchlosť prenosu tepla.

Príklady

- Príklady jazdy tepla

V tepelnej vodivosti sa tepelná energia prenáša zrážkami medzi atómami a molekulami materiálu, či už táto tuhá látka, kvapalina alebo plyn. 

Pevné látky sú lepšie tepelné vodiče ako plyny a kvapaliny. V kovoch existujú voľné elektróny, ktoré sa môžu pohybovať okolo kovu.

Pretože voľné elektróny majú veľkú mobilitu, sú schopné prenášať kinetickú energiu účinnejšie zrážkami, takže kovy majú vysokú tepelnú vodivosť.

Z hľadiska makroskopického hľadiska sa tepelná vodivosť meria ako množstvo tepla prenášaného na jednotku času alebo kalorického prúdu H:

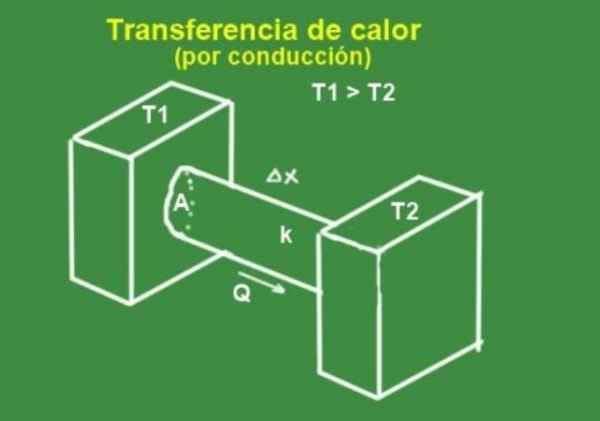
Obrázok 2. Vedenie tepla cez tyč. Pripravil Fanny Zapata.

Kalorický prúd H je úmerný prierezom Do a k zmene teploty na jednotku pozdĺžnej vzdialenosti.

Predchádzajúci vzorec je známy ako Fourierov zákon a proporcionalita konštanta klimatizovať Je to tepelná vodivosť. 

Táto rovnica sa používa na výpočet kalórií H tyče, ako je ten na obrázku 2, ktorý je medzi dvoma teplotnými nádržami Tón1 a Tón2 respektíve Tón1> T2.

Tepelná vodivosť materiálov

Nižšie je uvedený zoznam tepelnej vodivosti niektorých materiálov Watt na Kelvin: w/(m . K) 

Môže vám slúžiť: Galileo Galilei a jeho zákon o voľnom páde

Hliník -205

Meď -385

Striebro -400

Oceľ -50

Korkové alebo sklolaminát- 0,04

Betón alebo sklo -0.8

Drevo- 0,05 až 0,015

Vzduch - 0,024

- Príklady tepla konvekciou

Pri tepelnej konvekcii sa energia prenáša v dôsledku pohybu tekutiny, ktorá má pri rôznych teplotách rôzne hustoty. Napríklad, keď vriaca voda v hrnci, voda blízko dna zvyšuje svoju teplotu, takže sa rozširuje.

Táto dilatácia spôsobuje, že horúca voda vzrastie, zatiaľ čo studené nízke, aby zaberalo priestor, ktorý zanechal horúcu vodu, ktorá vyšplhala. Výsledkom je pohyb obehu, ktorý pokračuje, až kým sa teploty všetkých úrovní nie sú rovnaké.

Konvekcia je tá, ktorá určuje pohyb veľkých vzduchových hmotností atmosféry Zeme a tiež určuje obeh morských prúdov.

- Príklady tepla ožarovaním

V mechanizmoch prenosu tepla vedením a konvekciou sa vyžaduje prítomnosť materiálu, aby sa prenášali teplo. Na druhej strane, v mechanizme žiarenia môže teplo prechádzať z jedného tela na druhé cez prázdnotu.

Toto je mechanizmus, ktorým slnko pri vyššej teplote ako Zem prenáša energiu na našu planétu priamo prázdnotou priestoru. Žiarenie sa k nám dostane elektromagnetickými vlnami.

Všetky materiály sú schopné emitovať a absorbovať elektromagnetické žiarenie. Maximálna frekvencia emitovaná alebo absorbovaná závisí od teploty materiálu a uvedená frekvencia rastie s teplotou.

Prevažná vlnová dĺžka v emisnom alebo absorpčnom spektre čierneho tela sleduje Zákon, čo uvádza, že prevládajúca vlnová dĺžka je úmerná inverzii telesnej teploty.

Na druhej strane, sila (vo wattoch), s ktorým telo vyžaruje alebo absorbuje kalórií elektromagnetickým žiarením, je úmerná štvrtej výkonnosti absolútnej teploty. Toto je známe ako Stefan zákon:

P = εaσt4

V predchádzajúcom výraze σ Je to Stefanova konštanta a jej hodnota je 5,67 x 10-8 w/m2 Klimatizovať4. Do Je to oblasť povrchu tela a ε Je to emisivita materiálu, konštanta bez rozmerov, ktorej hodnota je medzi 0 a 1 a závisí od materiálu.

Môže vám slúžiť: izobarický proces: vzorce, rovnice, experimenty, cvičenia

Cvičenie

Zvážte lištu na obrázku 2. Predpokladajme, že tyč je dlhá 5 cm, polomer 1 cm a je to meď.

Tyč je umiestnená medzi dvoma stenami, ktoré udržiavajú jeho konštantnú teplotu. Prvá stena má teplotu T1 = 100 ° C, zatiaľ čo druhá je pri T2 = 20 ° C. Určiť:

do.- Hodnota tepelného prúdu h

b.- Teplota medenej tyče pri 2 cm, 3 cm a 4 cm od teplotnej steny T1.

Roztok

Keď je medená lišta umiestnená medzi dvoma stenami, ktorých steny si vždy udržiavajú rovnakú teplotu, možno povedať, že je v stacionárnom režime. To znamená, že tepelný prúd H má rovnakú hodnotu pre každú chvíľu.

Na výpočet tohto prúdu aplikujeme vzorec, ktorý sa týka prúdu H na teplotný rozdiel a dĺžku tyče.

Keďže bar je meď, vieme, že v tabuľke predtým ukázalo, že jej voucher tepelnej vodivosti K: 385 w/(m k).

Prierez je:

A = πr2 = 3,14*(1 × 10-2m)2 = 3,14 x 10-4 m2

Teplotný rozdiel medzi koncami tyče je

Δt = (100 ° C - 20 ° C) = (373k - 293k) = 80k

Δx = 5 cm = 5 x 10-2 m

H = 385 w/(m k) * 3,14 x 10-4 m2 * (80k /5 x 10-2 m) = 193,4 w

Tento prúd je rovnaký kedykoľvek v bare a kedykoľvek, pretože sa dosiahol stacionárny režim.

Riešenie B

V tejto časti sme požiadaní, aby sme vypočítali teplotu Tp v bode P umiestnený vo vzdialenosti Xp Pokiaľ ide o stenu Tón1.

Výraz, ktorý dáva kalorický prúd H bod P je:

H = k a (t1 -Tp)/(xp)

Z tohto výrazu je možné vypočítať Tp cez:

Tp = t1 - (H xp) / (k a) = 373 k - (193,4 w / (385 w / (m k) 3,14 x 10-4 m2))*Xp

TP = 373 K - 1620,4 (k/m) * xp

Vypočítajme teplotu Tp V pozíciách 2 cm, 3 cm a 4 cm, nahradenie numerických hodnôt:

  • Tp = 340,6k = 67,6 ° C; 2 cm z T1
  • Tp = 324,4 k = 51,4 ° C; 3 cm z T1
  • Tp = 308,2k = 35,2 ° C; 4 cm z T1

Odkazy

  1. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 5. Tekutiny a termodynamika. Editoval Douglas Figueroa (USB).
  2. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6. skrátene vydanie. Učenie sa.
  3. Lay, J. 2004. Všeobecná fyzika pre inžinierov. Húb.
  4. Mott, r. 2006. Tekutina. 4. Vydanie. Pearson Vzdelanie. 
  5. Podivné, ja. 2003. Meranie prírodného prostredia. Druhý. Vydanie. Cambridge University Press.
  6. Wikipedia. Tepelná vodivosť. Obnovené z: je.Wikipedia.com