Mechanická práca, čo je, podmienky, príklady, cvičenia

On mechanická práca Je definovaný ako zmena energetického stavu systému, spôsobená pôsobením vonkajších síl, ako je gravitácia alebo trenie. Mechanické pracovné jednotky v medzinárodnom systéme (SI) sú Newton X Metro alebo Joules, skrátene J.

Matematicky je definovaný ako skalárny produkt sily sily posunutím vektora. Jo F Je to konštantná sila a l Je to posun, oba vektory, práca W je vyjadrená ako: W = F ● l

postava 1. Zatiaľ čo atlét zvyšuje váhu, pracuje proti gravitácii, ale keď si zachováva váhu nehybnú, z hľadiska fyziky nerobí prácu. Zdroj: Needpix.com

Ak sila nie je konštantná, musíme analyzovať prácu vykonanú, keď sú posuny veľmi malé alebo diferenciálne. V tomto prípade, ak sa považuje za východiskový bod k bodu A a ako príchod na B, celková práca sa získa pridaním všetkých príspevkov k tomu istému. Toto je rovnocenné s výpočtom tohto integrálu:

A ako je uvedené na začiatku, za predpokladu, že došlo k zmene v systéme, bude to preto, že na ňom konajú sily zo zahraničia, preto:

Variácie v systéme Energy = práca vykonaná externými silami

ΔE = w_rozšíriť

Keď sa do systému pridá energia, w> 0 a keď sa odpočítava<0. Ahora bien, si ΔE = 0, puede significar que:

-Systém je izolovaný a neexistujú žiadne vonkajšie sily.

-Existujú vonkajšie sily, ale na systéme nerobia prácu.

Pretože variácia energie je rovnocenná s prácou vykonávanou vonkajšími silami, jednotka, ak je energia tiež joule. To zahŕňa akýkoľvek typ energie: kinetický, potenciál, tepelný, chemický a viac.

[TOC]

Podmienky, aby existovala mechanická práca

Už sme videli, že práca je definovaná ako skalárny produkt. Zoberme si definíciu práce vykonanej konštantnou silou a uplatníme koncept skalárneho produktu medzi dvoma vektormi:

W = F ● L = F.l.cos θ

Kde F Je to veľkosť sily, l Je to veľkosť posunu a θ Je to uhol, ktorý existuje medzi silou a posunom. Na obrázku 2 je príklad naklonenej vonkajšej sily pôsobiacej na blok (systém), ktorý vytvára horizontálne posunutie.

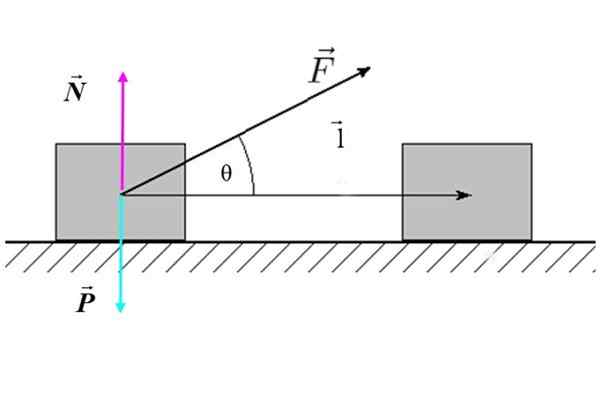Obrázok 2. Diagram voľného tela bloku, ktorý sa pohybuje na rovnom povrchu. Zdroj: f. Zapata.

Prepisovanie práce nasledovne:

W = (f. cos θ). l

Môžeme potvrdiť, že iba zložka sily rovnobežnej s posunom: F. cos θ eS schopný robiť prácu. Ak θ = 90 °, potom cos θ = 0 a práca by bola neplatná.

Preto sa dospelo k záveru, že sily kolmé na vytesnenie nerobia mechanickú prácu.

V prípade obrázku 2, ani normálna sila N ani váha P Pracujú, pretože obidve sú kolmé na vysídlenie l.

Známky práce

Ako je vysvetlené vyššie, W Môže to byť pozitívne alebo negatívne. Keď cos θ> 0, Práca vykonaná silou je pozitívna, pretože má rovnaký smer pohybu.

Môže vám slúžiť: hromadné číslo: Čo je to a ako ho získať (s príkladmi)

Jo cos θ = 1, pevnosť a posun sú paralelné a práca je maximálna.

V prípade cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Kedy cos θ = -1, Sila je úplne v rozpore s presídlením, ako je kinetické trenie, ktorého účinkom je zastaviť objekt, na ktorý koná. Práca je teda minimálna.

To súhlasí s tým, čo bolo povedané na začiatku: Ak je práca pozitívna, energia sa pridáva do systému a ak je negatívna, odpočíta sa.

Čistá práca W_slepo Je definovaný ako súčet diel vykonaných všetkými silami pôsobiacimi na systém:

W_slepo = ∑W_Jo

Potom môžeme dospieť k záveru, že na zaručenie existencie čistej mechanickej práce je potrebné, aby:

-Externé sily pôsobia na objekt.

-Tieto sily nie sú všetky kolmé na posun (cos θ ≠ 0).

-Práce vykonané každou silou nie sú navzájom zrušené.

-Existuje posun.

Príklady mechanickej práce

-Kedykoľvek sa vyžaduje, aby ste na základe odpočinku vložili objekt, je potrebné vykonať mechanickú prácu. Napríklad stlačte chladničku alebo ťažký kmeň na horizontálnom povrchu.

-Ďalším príkladom situácie, v ktorej je potrebné vykonať mechanickú prácu, je zmeniť rýchlosť pohybujúcej sa gule.

-Je potrebné robiť prácu na zdvihnutí predmetu v určitej výške na podlahe.

Teraz existujú rovnako bežné situácie, v ktorých Nie Práca sa vykonáva, hoci vzhľad naznačuje inak. Povedali sme, že na zvýšenie objektu v určitej výške musíme robiť prácu, takže načítame objekt, zdvihneme ho nad hlavu a necháme ho tam. Robíme prácu?

Zrejme áno, pretože ak je objekt ťažký, zbrane sa čoskoro unavujú, bez ohľadu na to, koľko práce sa vykonáva, práca sa nevykonáva z hľadiska fyziky. Prečo nie? Pretože objekt sa nepohybuje.

Ďalším prípadom, v ktorom, napriek vonkajšej sile, nevykonáva mechanickú prácu, keď má častica rovnomerný pohyb kruhu.

Môže vám slúžiť: Normálne úsilie: z čoho sa skladá, ako sa vypočíta, príklady

Napríklad dieťa, ktoré otočí kameň viazaný na šnúru. Napätie šnúry je centripetálna sila, ktorá umožňuje rotáciu kameňa. Ale vždy je táto sila kolmá na posun. Potom nerobte mechanickú prácu, napriek tomu, že uprednostňuje pohyb.

Cinetika pracovnej energie

Kinetická energia systému je to, čo má pod jeho pohybom. Jo m je cesto a vložka Je to rýchlosť pohybu, kinetická energia je označená Klimatizovať A je daný:

K = ½ mv²

Podľa definície kinetická energia objektu nemôže byť negatívna, pretože hmotnosť aj štvorec rýchlosti sú vždy kladné sumy. Kinetická energia môže byť 0, keď je objekt v pokoji.

Na zmenu kinetickej energie systému je potrebné-. Z tohto dôvodu je preto potrebné vykonávať čistú prácu v systéme, preto:

W_slepo = ΔKlimatizovať

Toto je práca Work - Kinetic Energy. Uvádza, že:

Čistá práca je rovnocenná s zmenou kinetickej energie systému

Všimnite si, že hoci je k vždy pozitívny, AK môže byť pozitívny alebo negatívny, pretože:

ΔK = k_Konečný - Klimatizovať _{počiatočný}

Jo Klimatizovať_Konečný >Klimatizovať _{počiatočný} Systém získal energiu a ΔK> 0. Naopak, áno Klimatizovať_Konečný < Klimatizovať _{počiatočný}, Systém priniesol energiu.

Práca vykonaná na natiahnutí jari

Pri natiahnutí (alebo komprimovaní) pružiny je potrebné urobiť prácu. Táto práca je uložená na jar, čo umožňuje to, aby sme mohli pracovať, napríklad na blok, ktorý je pripojený k jednému z jeho koncov.

Hookeov zákon uvádza, že sila, ktorú vyvíjajú pružinou. Konštanta proporcionality závisí od toho, ako je pružina: mäkká a ľahko deformovateľná alebo rigidná.

Táto sila je daná:

F_r = -KX

Vo výraze, F_r Je to sila, klimatizovať Je to jarná konštanta a X Je to posun. Záporné znamenie naznačuje, že sila vyvíjaná pružinou je proti posunu.

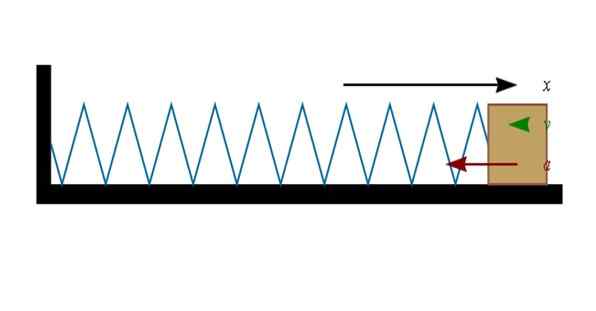Obrázok 3. Stlačená alebo roztiahnutá pružina funguje na predmete zviazanom ku koncu. Zdroj: Wikimedia Commons.

Ak je pružina stlačená (doľava na obrázku), blok na konci sa presunie doprava doprava. A keď je pružina natiahnutá (vpravo), blok sa bude chcieť presunúť doľava.

Na komprimovanie alebo natiahnutie pružiny musí urobiť nejaký externý agent túto prácu a keďže je to variabilná sila, vypočítať túto prácu, musíte použiť definíciu, ktorá sa vyskytla na začiatku:

Môže vám slúžiť: Darcy Law

Je veľmi dôležité poznamenať, že toto je práca vykonaná externým agentom (napríklad ruka osoby) na stlačenie alebo natiahnutie pružiny. Preto sa negatívny znak neobjaví. A keďže pozície sú štvorcové, bez ohľadu na to, či ide o kompresie alebo predĺženia.

Práca, ktorá urobí pružinu zase blok, je:

W_jar = -W_rozšíriť

Cvičenia

Cvičenie 1

Blok na obrázku 4 má hmotnosť m = 2 kg a prechádza cez naklonenú rovinu bez trenia, s a = 36.9. Za predpokladu, že sa nechá skĺznuť z zvyšku z vrcholu roviny, ktorej výška je H = 3 m, nájdite rýchlosť, s ktorou blok dosahuje základňu lietadla, cez kinetickú energetickú energiu.

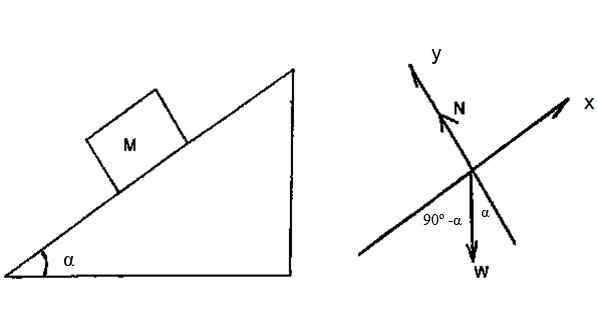Obrázok 4. Blok sa skĺzne dole na naklonenej rovine bez trenia. Zdroj: f. Zapata.

Riešenie

Diagram voľného tela ukazuje, že jedinou silou schopnou pracovať na bloku je váha. Presnejšie: Zložka hmotnosti pozdĺž osi x.

Vzdialenosť prevezená blokom v rovine sa vypočíta trigonometrím:

D = 3 / (cos 36.9 °) m = 3.75 m

W_váha = (Mg). d. cos (90-a) = 2 x 9.8 x 3.75 x cos 53.1. j = 44.1 j

Pracovnou kinetickou energiou vety:

W_slepo = ΔKlimatizovať

W_slepo = W_váha

ΔK = ½ mV_F²- ½ MV_ani²

Pretože je prepustený z odpočinku, vložka_ani = 0, preto:

W_slepo = ½ mv_F²

Cvičenie 2

Horizontálna pružina, ktorej konštanta je K = 750 N/m, je pripevnená o jeden koniec k stene. Jedna osoba komprimuje druhý koniec vzdialenosť 5 cm. Vypočítajte: a) sila, ktorú vyvíjala osoba, b) práca, ktorú urobil na stlačení pružiny.

Riešenie

a) Rozsah sily použitej osobou je:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Ak je pružinový koniec pôvodne v x₁ = 0, odtiaľ to odtiaľ do konečnej polohy x₂ = 5 cm, je potrebné vykonať nasledujúce práce, podľa výsledku získaného v predchádzajúcej časti:

W_rozšíriť = ½ K (x₂² - X₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 2. Dynamika. Editoval Douglas Figueroa (USB).
2. Iparraguirre, L. 2009. Základná mechanika. Zbierka a matematika prírodných vied. Bezplatná online distribúcia.
3. Rytier, r. 2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
4. Fyzikálne librettexts. Veta pracovnej energie. Získané z: Phys.Librettexts.orgán
5. Práca a energia. Obnovené z: fyziky.BU.Edu
6. Práca, energia a sila. Získané z: NCERT.Vhodný.v